18.2. Швидкість росту бульбашок на твердій поверхні

Після того як зародок, який виник в активній впадині, досяг устя впадини і утворив над нею склепіння, при відповідних умовах буде відбуватися ріст зародка до макроскопічних розмірів. Умови початку кипіння розглянуті раніше. Зараз варто зупинитися на питанні про швидкість росту парової бульбашки на поверхні нагріву. Строгий аналітичний опис і розв’язок цієї задачі представляють великі труднощі. Ця задача з ряду причин значно складніша задачі про ріст бульбашки в об’ємі рівномірно перегрітої рідини.

Форма бульбашки, яка росте на поверхні нагріву, у більшій чи меншій мірі відрізняється від сферичної і змінюється під час росту. Більш складні, ніж у випадку об’ємного кипіння, умови підводу теплоти. При визначенні теплового потоку, який проходить крізь міжфазну границю, необхідно враховувати підвід теплоти до рідини від поверхні нагріву і температурну нерівномірність у прилеглих до твердої поверхні шару перегрітої рідини.

Парова бульбашка, досягнувши певного розміру, відривається від поверхні, а вивільнений нею об’єм заповнюється рідиною. Відрив бульбашок відбувається періодично з певною частотою. У період циклу від відриву даної бульбашки до відриву наступної за нею відбувається нестаціонарний теплообмін між поверхнею нагріву і рідиною. При розвиненому кипінні має місце взаємний вплив сусідніх бульбашок, які також у певній мірі впливають на гідродинамічні і теплові умови процесу. Все це обумовлює виняткову складність задачі, робить практично неможливим коректний і повний її теоретичний аналіз, і призводить до необхідності прийняття спрощених моделей, які дозволяють отримати наближений розв’язок задачі.

Форма зростаючої бульбашки залежить від ряду факторів, які сильно відмінні для змочуваних і не змочуваних рідин і змінюється в часі. Але якщо обмежитися розглядом найбільш широко використовуваних у техніці змочуваних рідин, то головним фактором, який визначає форму бульбашки, можна вважати приведений тиск π = р/р_кр, за якого відбувається кипіння.

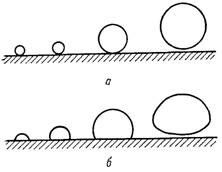
Рис.18.3. Форма бульбашок, які ростуть на твердій поверхні

У деякій області середніх значень π утворюються бульбашки різної форми – близькі до сфери чи на півсфери, сплющені, а в певні моменти часу (перед відривом) і витягнуті. Для води – цей тиск близький до атмосферного. Але при порівняно невеликому підвищенні тиску (до 0,5...1,0 МПа) форма бульбашок при кипінні води стає близькою до сферичної. Взагалі в області високих приведених тисків для змочуваних рідин характерна близька до сфери форма бульбашок (зрізана сфера) (рис.18.3,а). В області низьких значень π характерною формою бульбашок стає близька до на півсфери (рис.18.3,б). Це пояснюється головним чином зміною густини пари і пов’язаних з нею швидкості росту бульбашки. З підвищенням тиску швидкість росту в абсолютному виразі зменшується, прямуючи до нуля при критичних тисках. При високих значеннях π відбувається повільний (квазістатичний) ріст бульбашки, і в цьому випадку інерція рідини на форму бульбашки практично не впливає. При низьких значеннях π швидкість росту бульбашки велика, динамічні ефекти поверхневого натягу і гравітації будуть

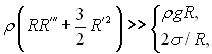(18.33)

а вплив інерції рідини, що викликає деформацію бульбашки і її сплющення, проявляється в більшій мірі. Бульбашка набуває форму близьку до на півсфери.

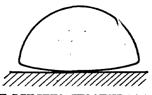
Рис.18.4. Схема утворення мікрошару в основі бульбашки, що росте

Тому що ковзання рідини відносно твердої поверхні відбуватися не може то на ній формується тонкий шар рідини – мікрошар (рис.18.4), а над ним напівсферичний купол. При кипінні на поверхні нагріву так само, як і при об’ємному кипінні, практично вся видима стадія росту бульбашок є асимптотичною і визначається умовами підводу теплоти до зростаючої бульбашки при тиску пари в ній, який мало відрізняється від тиску в системі. На цій засаді перші моделі процесу і методи розрахунку будувалися припущенні, що ріст парової бульбашки на поверхні нагріву приблизно можна описати такими ж залежностями, якими характеризується ріст бульбашки в об’ємі перегрітої рідини, чи співвідношеннями аналогічними їм. Ці припущення ґрунтувалися на тому, що під час росту бульбашка витісняє з пристінного шару перегріту рідину і навколо бульбашки утворюється тонкий його шар (рис.18.5). Вважалося, що під час росту бульбашки основна кількість теплоти передається крізь міжфазну границю по контуру АВС внаслідок охолодження перегрітого шару рідини, а підвід теплоти від поверхні нагріву до рідини у нижній частині бульбашки можна не враховувати.

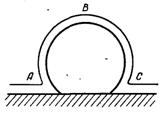
Рис.18.5. Схема витіснення пристінного шару рідини бульбашкою, під час її росту

Д.А.Лабунцов, оцінивши запас ентальпії, який відповідає перегріву рідини у пограничному шарі, показав що у загальному випадку така модель неприйнятна. Навіть у граничному випадку, вважаючи, що шар рідини по всій товщині δ перегрітий на ΔТ = Т_с – Т_н, кількість теплоти, яка може передаватися бульбашці відповідає πR²δρcΔТ. З рівняння теплового балансу слідує, що за рахунок цієї кількості теплоти бульбашка може вирости тільки до розміру

(18.34)

При середніх і високих тисках число Ja < 1. Тоді з рівняння (18.34) слідує, що при цих тисках бульбашка не може вирости за межі пограничного шару, що не відповідає дійсності.

Однак в області вакууму при великих значеннях чисел Ja >> 1і високих перегрівах роль підведення теплоти до бульбашки з обмежуючого її шару перегрітої рідини стає суттєвою і збільшується зі збільшенням вакууму.

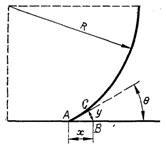
Рис.18.6. Величини, які відтворюють співвідношення локальної густини теплового потоку

У протилежність цьому допущенню Лабунцов запропонував схему, яка ґрунтується на уяві, що при середніх і високих тисках визначальну роль у процесі росту бульбашки відіграє підвід теплоти в нижню частину бульбашки біля її основи. Згідно цієї схеми (рис.18.6) теплота передається від стінки до нижньої частини міжфазної границі теплопровідністю через клиновий кільцевий шар рідини АВС. Рівняння росту бульбашки, яке відповідає цій моделі, має вид:

(18.35)

де β  – числовий коефіцієнт, який визначається дослідним шляхом.

Якщо прийняти β  = 6, то рівнянням (18.35) можна задовільно узагальнити дослідні дані при кипінні води (0,1...10 МПа), бензолу (0,1...1,5 МПа) і етанолу (0,1...3,4 МПа) на срібних і мідних поверхнях нагріву.

У загальному випадку ріст бульбашки на поверхні нагріву визначається обома факторами – підводом теплоти від твердої поверхні до основи бульбашки (рис.18.5) і випаровуванням з криволінійної поверхні бульбашки (рис.18.6). Відносна роль цих факторів залежить від умов процесу, перед усім – від тиску і проміжку часу від початку росту бульбашки. Тому вихідним рівнянням для розв’язку задачі є рівняння теплового балансу, яке враховує вплив обох факторів:

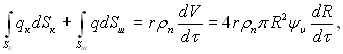(18.36)

де – об’єм сферичного сегмента радіусом R.

Перший доданок лівої частини (18.36) враховує підвід теплоти до бульбашки крізь верхню криволінійну поверхню бульбашки (поверхня куполу S_к), другий – підвід теплоти до бульбашки в її основі від поверхні нагріву крізь прилеглий до неї тонкий шар рідини. Визначення обох складових лівої частини теплового балансу представляє значну трудність .

При розрахунку приходиться ідеалізувати форму бульбашки і розглядати її як частину сфери у загальному випадку з деяким “динамічним” крайовим кутом, який враховує відхилення крайового кута від рівноважного кута змочування. Дуже важкий (практично поки що неможливий) коректний облік нерівно важності температурного поля у пристінному шарі рідини. Ця нерівно важність чи не враховується взагалі, чи враховується прийняттям певного ефективного перегріву ΔТ' (меншого за ΔТ_с), за яким розраховується число Ja'. Величина q_к зазвичай визначається за рівнянням росту бульбашки в об’ємі рідини, а величина S_к – чи як площа поверхні сферичного сегменту, чи як пропорційна їй величина. В наслідок цього перша складова теплового потоку (18.36) набуває виду:

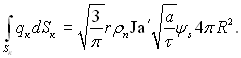(18.37)

Внаслідок інструментальних досліджень було виявлено значні флуктуації температури поверхні біля центру пароутворення при кипінні води під атмосферним тиском. Це підтвердило висновок про існування під бульбашкою мікрошару рідини товщиною порядку мікронів. Швидке місцеве охолодження поверхні, обумовлене дуже інтенсивним відводом теплоти внаслідок випаровування мікрошару.

Наближений розв’язок складної задачі про формування і товщину мікрошару δ отримано, виходячи з уяви про переважний вплив на величину δ в’язкості рідини, нерухомості мікрошару відносно твердої поверхні і аналогії між початковою товщиною δ₀ і товщиною витіснення пограничного шару:

(18.38)

де δ₀ – товщина мікрошару біля зовнішньої границі основи бульбашки в момент часу δ₀, що відлічується від початку росту бульбашки; ν  – кінематична в’язкість рідини; С – стала, середнє значення якої 0,8 (залежить від показника степеня п в рівняння R ~ τⁿ і змінюється від 0,6 до 1,1). Виходячи з таких уявлень про процес отримано рівняння росту півсферичної бульбашки з урахуванням ефекту випаровування мікрошару. Вважалося, що у загальному випадку коефіцієнти теплозасвоєння (λсρ)^0,5 металу стінки і рідини можна спів ставляти між собою, а температура твердої поверхні змінна. Для цих умов отримано наступне рівняння:

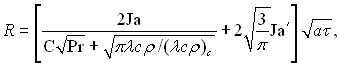(18.39)

де

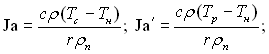
Т_с і Т_р – початкова температура поверхні нагріву і рідини відповідно.

Рівняння (18.39) відображає ступінь впливу мікрошару на швидкість росту бульбашки на початковій нетривалій стадії і не відноситься до всього періоду росту бульбашки на поверхні нагріву аж до відриву її від поверхні. Порівняння його з небагато чисельними дослідними даними з росту бульбашки на цій стадії показує, що дослідні значення коефіцієнта біля τ^0,5 дуже близькі до тих, які слідують з (18.39).

Наші уявлення про постійність локальної товщини і поверхні випаровування мікрошару далекі від реальної картини. У дійсності внаслідок випаровування відбувається зменшення товщини шару і його висихання (від центра до периферії); поверхня випаровування зменшується, а розпір сухої плями під бульбашкою збільшується. Зменшення товщини шару сприяє росту бульбашки, а скорочення поверхні випаровування впливає у протилежному напрямку. Вплив першого фактора у певній мірі компенсується впливом другого.

Рівняння (18.39) заслуговує уваги тому, що воно містить у собі відношення коефіцієнтів теплостійкості матеріалу поверхні нагріву і рідини, чим ураховується вплив теплофізичних властивостей поверхні нагріву на ріст парових бульбашок і на теплообмін при кипінні.

Утворення півсферичних бульбашок і формування мікрошару характерні для невеликих приведених тисків киплячої рідини на початковій стадії росту бульбашки. Зі збільшенням радіуса мікроскопічної бульбашки ріст її сповільнюється, вона виходить своєю верхньою частиною за межі перегрітого шару рідини, вплив інерції рідини зменшується, відбувається поступова зміна форми бульбашки, і після деякої проміжної стадії її форма буде визначатися співвідношенням сил поверхневого натягу і гравітації і на стадії квазістатичного росту наближатися до зрізаної сфери.

Основа бульбашки (суха пляма під нею) при висиханні мікрошару розширюється, а далі при досягненні певного максимального значення скорочується. Підвід теплоти до бульбашки буде відбуватися від перегрітого шару рідини на криволінійній поверхні її куполу і від поверхні нагріву через кільцевий шар біля основи бульбашки.

З підвищенням приведеного тиску π можливість утворення мікрошару і його роль зменшуються і, починаючи з деякого значення π, стають дуже малими. З цього виходить, що умови росту бульбашки дуже складні і багатогранні. Вони залежать від багатьох факторів (передусім від тиску) і, що дуже суттєво, різні у різні періоди росту бульбашки.

Дослідні дані стосовно росту бульбашок на твердій поверхні задовільно узагальнюються залежністю R(τ) запропонованій В.В.Яговим. При її отриманні враховувались і тепловий вплив поверхні нагріву, і теплопідвід від криволінійної поверхні бульбашки. Внесок тепловідводу від твердої поверхні враховувався на підставі уявлень А.А.Лабунцова, а тепловий потік крізь криволінійну поверхню визначався, виходячи з уяви, що площа поверхні з інтенсивним випаровуванням, утворена виштовхуванням перегрітого шару рідини, приблизно дорівнює площі основи бульбашки. Внаслідок опрацювання дослідних даних отримана наступна залежність:

(18.40)

яка містить у собі два числових коефіцієнта β і γ. У відповідності з дослідними даними при р > 0,1 МПа, прийнято, що β = 6; γ є функцією крайового кута θ і при його зміні від 40 до 90° змінюється від 0,1 до 0,49. Середнє значення γ=0,3.

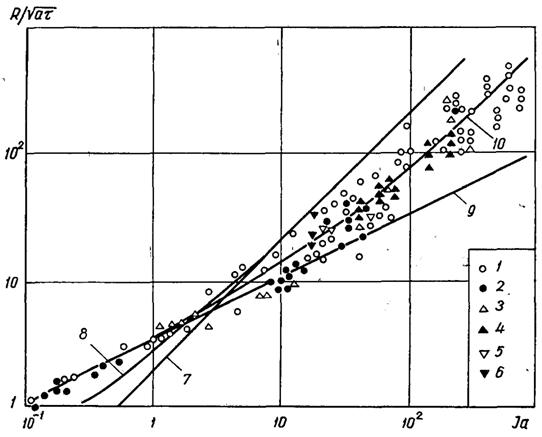
Рис.18.7. Співставлення дослідних даних залежності модуля росту парових бульбашок від числа Ja: 1 – вода; 2 – етанол; 3 – бензол; 4 – метанол; 5 – пентан; 6 – азот; з розрахунковими даними за формулами: 7 – (18.22); 8 – (18.27); 9 – (18.35); 10 – (18.40)

На рис.18.7 наведено співставлення дослідних і розрахункових (за різними формулами) значення модуля росту парових бульбашок R/(aτ)^0,.5 у залежності від числа Ja. З рисунка видно, що формула (18.40) дає краще, ніж інші формули, погодження середнього безрозмірного модуля росту з дослідними даними різних авторів для широкого інтервалу тисків і різних рідин. При Ja << 1 (високий тиск) асимптота співвідношення (18.40) має вид:

(18.41)

який співпадає з (18.35) і відповідає урахуванню теплопідводу тільки від твердої поверхні.

При Ja >> 1 (низький тиск) граничне співвідношення набуває виду

(18.42)

аналогічного співвідношенням для росту бульбашки в об’ємі перегрітої рідини.

В області дуже низьких тисків (р ≤ 10 кПа) при числах Якоба близьких чи більших 1000, у значній мірі проявляється вплив динамічних ефектів на форму бульбашки і температурний напір. Для цієї області можна використовувати аналогічні за структурою рівняння (18.32) тільки з іншими значеннями коефіцієнтів А і В.

З формули (18.40) і розташування дослідних точок на рис.18.7 видно, що залежність R/(aτ)^0,5 від Ja має нелінійний характер. Ця не лінійність обумовлена наявністю двох шляхів підводу теплоти, які відрізняються різними закономірностями, і зміною відносного впливу їх на ріст бульбашки зі зміною числа Ja.

Формула (18.40) отримана за умови постійності температури твердої поверхні без урахування впливу теплофізичних властивостей матеріалу поверхні. У деяких випадках, наприклад, при кипінні кріогенних рідин, цей вплив може бути суттєвим. Тому отримані для цього випадку залежності для росту бульбашки мають такий вид R = C(τ)^0,5, де С залежить не тільки від властивостей рідини, але і від властивостей матеріалу поверхні нагріву.

На сьогоднішній день накопичено багато дослідних даних зі зміни розмірів окремих парових бульбашок під час кипіння на твердій поверхні нагріву. При кипінні насиченої рідини ріст бульбашки на поверхні закінчується її відривом від поверхні. Під час відриву бульбашка, спливаючи, тягне за собою шар перегрітої рідини. Вивільнений нею об’єм замінюється відносно холодною рідиною і починається період очікування, на протязі якого внаслідок нестаціонарного теплообміну між стінкою і рідиною відбувається перегрів рідини. Після того, коли досягнуто необхідного перегріву рідини, у впадині виникає новий зародок і далі починається ріст нової парової бульбашки.

Кипіння рідини на поверхні нагріву може відбуватися також при недогріві основної її маси до температури насичення. Такий вид кипіння часто використовують у технічних пристроях для відводу теплових потоків великої густини. Процес розвитку парових бульбашок при кипінні з недогрівом відрізняється суттєвими особливостями в порівнянні з ростом бульбашок у насиченій рідині. Парові бульбашки спочатку ростуть, досягають максимального розміру, а далі деградують. В умовах вільного руху рідини в залежності від недогріву і тиску вони чи відриваються від поверхні і конденсуються в холодному ядрі рідини, чи не відриваються і захлопуються на самій поверхні. Так, при атмосферному тиску і дуже малій швидкості води 0,1...0,2 м/с отримано, що при невеликих недогрівах до 20 К відбувається відрив бульбашок від стінки, а при недогрівах понад 40 К значна частина бульбашок, які пройшли стадію росту до максимального розміру, швидко деградують аж до повного зникнення, не відриваючись від стінки.

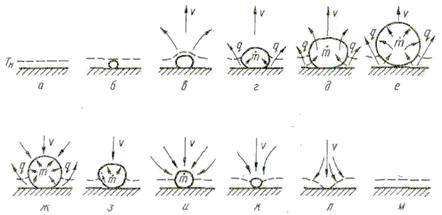
Рис.18.8. Якісна картина росту парових бульбашок при кипінні не догрітої рідини

Якісна картина стадій процесу росту і деградації парових бульбашок на протязі одного циклу при кипінні з недогрівом наведена на рис.18.8. Пунктирні лінії показують межі перегрітого шару рідини, а стрілками – напрямок потоку теплоти і маси. Момент б відповідає миті виникнення зародка. У момент в і г бульбашка росте внаслідок випаровування рідини. В момент г у верхній частині бульбашки температура рідини дорівнює Т_н і випаровування там припиняється. У момент д і е у бульбашці відбуваються протилежні процеси – внизу вона росте внаслідок випаровування, зверху зменшується внаслідок конденсації. У момент е ефект конденсації дорівнює ефекту випаровування, бульбашка досягає максимального розміру. Після того як ефект конденсації перевищує ефект випаровування, відбувається зменшення розміру бульбашки (моменти ж...к) аж до її повного зникнення (моменти л і м). У цей період до поверхні нагріву надходить холодна рідина, далі відбувається її перегрів, і цикл зародження, росту, зменшення і зникнення бульбашки повторюється.