Розділ 19. ВНУТРІШНІ ХАРАКТЕРИСТИКИ БУЛЬБАШКОВОГО КИПІННЯ
19.1. Відривний розмір парової бульбашки
При кипінні насиченої рідини парова бульбашка, яка розвинулася з життєздатного зародка, росте на поверхні нагріву до певного розміру, досягнувши якого відривається від твердої поверхні і спливає, виштовхуючи деяку кількість перегрітої рідини. Вивільнений бульбашкою об’єм заповнюється новими порціями більш холодної рідини, далі відбувається її нагрів, внаслідок чого поновлюються температурні умови, які забезпечують утворення нового зародка з подальшим ростом парової бульбашки. Цей процес відбувається з певною періодичністю, яка характеризується частотою f відриву бульбашки від поверхні нагріву.
Час повного циклу τ від відриву даної бульбашки до відриву наступної складається з часу існування бульбашки на поверхні нагріву від моменту його зародження до відриву τ1 і часу очікування τ2, на протязі якого відбувається поновлення температурних умов, які необхідні для виникнення нового зародка. Таким чином, у загальному випадку τ = τ1 + τ2, а f = 1/τ = 1/(τ1 + τ2). Розмір бульбашки при її відриві від твердої поверхні характеризується відривним діаметром dв сфери, об’єм якої дорівнює об’єму бульбашки, що відірвалася, тому що форма бульбашки у момент відриву відхиляється від сферичної.
Швидкість росту бульбашки у даний момент R′ = dR/dτ (де R – поточний радіус), зміна її розміру і форми, періоди τ, τ1, τ2, відривний діаметр dв, частота відриву f і добуток dвf , який представляє собою середню швидкість росту парової бульбашки w'' за період τ, є внутрішніми характеристиками процесу бульбашкового кипіння, специфічними характеристиками цього процесу. При аналізі питання про закономірності теплообміну при кипінні важливе значення мають такі внутрішні характеристики, як dв, f і особливо dвf.
При рішенні задачі про теплообмін під час кипіння на реальних поверхнях нагріву достатнього розміру не можна обмежитися характеристиками одиночних бульбашок, а необхідно вводити до розглядуваних характеристик ансамбль виниклих на цій поверхні бульбашок – осереднені для ансамблю відривні діаметри, частоти відриву і середні швидкості росту парових бульбашок.
Теоретичне рішення задачі про відривний діаметр парової бульбашки у її загальній і коректній постановці представляє великі труднощі. Під час росту парової бульбашки відбувається зміна не тільки її об’єму, але і форми. При досягненні певного розміру бульбашки її форма стає нестійкою. Незначні подразнення, у тому числі навіть симетричні осі, можуть вивести її з рівноважного стану і привести до зміни форми, замиканню міжфазної границі рідина – пара і відрив бульбашки чи від твердої поверхні, чи від парового прошарку, який залишає бульбашка, що відірвалася від поверхні. Проміжок часу τ′ між початком втрати стійкості форми бульбашкою, до її відриву дуже малий, але кінцевий. Але із-за нетривалості τ′ і труднощів його визначення τ′ зазвичай включають до періоду росту τ1 і окремо не враховують.
Наведені раніше методи розв’язку задачі про швидкість росту парової бульбашки ґрунтуються на тій уяві, що форма бульбашки залишається під час її росту подібною до вихідної форми (сферичного сегменту). Вони не містять формул зв'язку між об’ємом і формою бульбашки під час її росту, про втрату стійкості, про умови замикання границі рідина – пара і про мить відриву бульбашки.
Задача про форму бульбашки, яка росте і відривається, достатньо складна навіть у самій простій статичній постановці для симетричної відносно вертикальної осі форми бульбашки. Відомі з теорії капілярності рівняння, які визначають форму поверхні бульбашки чи краплі, отримані на підставі рівноваги сил. У статичній задачі розглядаються тільки підйомна архімедова сила і сила поверхневого натягу. Навіть у цьому порівнянно простому випадку для рівноважної форми нерухомої у місці контакту з гладкою поверхнею бульбашки при даному куті змочування θ отримується досить складне диференціальне рівняння:
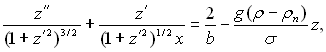(19.1)
де z і х – координати у напрямку вертикальної осі і радіуса відповідно (рис.19.1) (початок координат на вершині бульбашки); z' = dz/dx; z'' = d2z/dx2; b – радіус кривизни на вершині бульбашки.
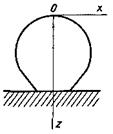
Рис.19.1. До визначення осей координат до рівняння (19.1)
В.Фрітц на підставі опрацювання табличних даних Ф.Бешфорса (для визначення форми і величини бульбашок повітря у воді при температурі 20 °С) отримав конкретне безрозмірне співвідношення для максимального об’єму парової бульбашки. Де показано, що кожному значенню радіуса основи бульбашки х (кругу дотику бульбашки з твердою поверхнею) теоретично відповідає два рівноважних об’єми бульбашки. Більший об’єм мають бульбашки з перегином у меридіальній площині. При певному значенні х верхня і нижня криві залежності V(x) змикаються. Відмічено існування максимально можливого в умовах рівноваги об’єму бульбашки. Величина цього об’єму Vmax залежить від фізичних властивостей рідини і її пари і крайового кута змочування θ. Опрацювання табличних даних виконана В.Фрітцом в безрозмірних координатах
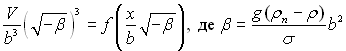(рис.19.2)
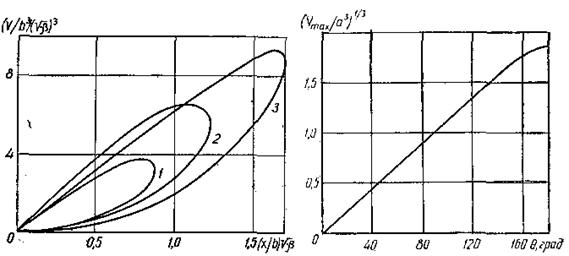
↑Рис.19.2. Графічне представлення Фрітцем табличних даних Бешфорса при θ: 1 – 90; 2 – 111; 3 – 125°
Рис.19.3. Залежність безрозмірного максимального розміру бульбашок від величини крайового кута ↑
Приймаючи до уваги, що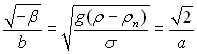 
, де а – капілярна стала Лапласа, 
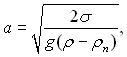на підставі даних наведених на рис.19.2, складені таблиці Vmax/a3 у залежності від
θ і графік залежності (Vmax/a)1/3 від
θ (рис.19.3).
Якщо апроксимувати криву (рис.19.3) прямою лінією і прийняти, що максимальний і відривний об’єми бульбашки рівні (Vmax = Vв), і виразити Vв як об’єм рівновеликої кулі, то можна отримати просте розрахункове співвідношення для визначення величини відривного діаметра бульбашки dв, яке відоме як формула Фрітца:
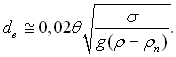(19.2)
На протязі тривалого часу вважалося, що формулу Фрітца можна застосовувати також для реальних умов бульбашкового кипіння рідини на поверхні нагріву. Перед усім варто зауважити, що формула (19.2) містить у собі величину статичного кута змочування θ, від якої сильно залежить dв. Тому для її використання необхідно мати достовірні дані про величину θ для різних рідин при різних тисках. Між тим дані про θ дуже скупі, недостатньо надійні і суперечні. Навіть для такої розповсюдженої рідини як вода, залишається невиясненим основне питання – залежність θ від тиску чи температури на лінії насичення. Виконані дослідження при кипінні води на різних поверхнях (мідь, сталь, нікель) в інтервалі тисків 0,1...1,5 МПа виявили помітне зменшення θ з ростом тиску насичення. Величина θ вийшла зворотно пропорційною рн приблизно у степені 0,3 (рис.19.4).
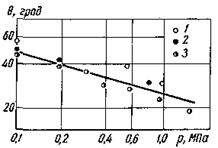
Рис.19.4. Вплив тиску на крайовий кут при кипінні води на поверхнях з різних матеріалів: 1 – мідь; 2 – сталь; 3 – нікель
Недостатність і протиріччя стосовно θ пояснюються багатьма причинами, у тому числі трудністю точного визначення θ в умовах бульбашкового кипіння і помітним впливом на θ незначних забруднень поверхні нагріву (окислами, жировими відкладеннями і іншими домішками). Дослідне визначення θ більш складне, ніж безпосереднє вимірювання розмірів бульбашок, які відриваються від поверхні теплообміну.
Але справа криється не тільки в практичних труднощах при використанні рівняння (19.2), але і в тому, що умови процесу бульбашкового кипіння суттєво відрізняються від умови статичної задачі. У різних центрах пароутворення на реальній поверхні нагріву ростуть і відриваються парові бульбашки різних розмірів. Ріст їх відбувається з кінцевою і змінною швидкістю, виникає інерція рідини, яка не враховується рівнянням (19.1). Бульбашки взаємодіють одна з іншою і підлягають гідродинамічній дії з боку рідини. Тому формулу (19.2) не можна застосовувати для умов бульбашкового кипіння, що підтверджується наявними даними про відривні діаметри бульбашок.
Питання еволюції форми бульбашки, її стійкості і визначення відривного розміру бульбашки при її квазістатичному рості на горизонтальній поверхні розглядалися багатьма дослідниками. У роботах Е.І.Несіса в основу покладено варіант поверхні бульбашки з її висотою в якості параметра, отриману варіаційним методом на підставі принципу мінімуму повної енергії. Внаслідок аналізу цього рівняння було виявлено якісні особливості взаємозв’язку висоти (об’єму) бульбашки і розміру її основи, розглянуто вплив крайового кута на механізм відриву бульбашки. Показано, що з ростом бульбашки розмір основи спочатку збільшується, а після досягнення максимального розміру – зменшується. При малих крайових кутах основа зменшується до нуля, при великих (у випадку плохого змочування) – відрив бульбашки відбувається по уточненій частині із залишком частини парового об’єму на твердій поверхні.
Наведені методи і розв’язки стосуються граничного випадку квазістатичного росту і відриву одиночної бульбашки, коли можна обмежитися урахуванням тільки підйомної архімедової сили і сили зчеплення з поверхнею, обумовленою поверхневим натягом. Квазістатичний режим відриву бульбашки характерний для області високих приведених тисків рідини. Зі зменшенням тиску усе з більшим ступенем проявляється вплив динамічних ефектів, і при низьких тисках, особливо в умовах вакууму, вони стають переважними. Перехід від квазістатичного до динамічного режиму відриву бульбашок відбувається плавно зі зменшенням тиску. Тому існує достатньо широка перехідна область, де вплив на відрив бульбашки різних факторів за величиною можна співставити між собою.
В останні роки з’явилося ряд робіт, в яких задача відриву бульбашки розглядається у динамічній постановці з урахуванням сил інерції і опору рідини. Але розрахункова схема, яка прийнята у більшості робіт, незадовільна. Вона зводиться до того, що записуються вирази для діючих на бульбашку сил: підйомної, поверхневого натягу, лобового опору, інерції рідини, а далі з умови рівноважності всіх сил, включаючи силу інерції, визначається відривний діаметр. Варто зауважити, що силу опору, яку необхідно вводити до розрахунку, значно менша лобового опору під час руху бульбашки обмеженої рідиною, і коректне її визначення представляє великі труднощі.
Більш обґрунтований підхід до рішення задачі вбачається в початковому розв’язку гідродинамічної задачі, яка зводиться до того, що виникла в об’ємі рідини бульбашка розглядається як така, що росте і одночасно спливає, збільшуючи свій об’єм. Швидкість об’ємного розширення задана. Рівняння балансу сил набуває виду:
(19.3)
Вважаючи, що ріст бульбашки відбувається за степеневим законом
(19.4)
при постійному п, рівному 0,5, і враховуючи, що ρп << ρ, а w = ds/dτ (де s – координата центра маси бульбашки). Баланс сил записується у вигляді диференціального рівняння, яке пов’язує s і τ:
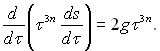(19.5)
Розв’язуючи це рівняння при початкових умовах R(0) = 0 і s(0) = 0, отримаємо:
(19.6)
Далі це рішення застосовуємо до бульбашки, яка росте на поверхні нагріву. При цьому у відповідності з дослідними спостереженнями вважаємо, що бульбашка спочатку має півсферичну форму. Вважаємо також, що стінка діє як наполовину обмежений масив рідини, показник степеня п в (19.5) становить 0,5, бульбашка в момент відриву має сферичну форму і s(τв) = Rв. Тоді з (19.6) виходить, що Rв = 0,4gτв2. Таким чином отримується друге рівняння, яке пов’язує R і τ.
Співвідношення Rв = 0,4gτв2 зі скоректованим числовим коефіцієнтом (0,6 замість 0,4) задовільно (з точністю 30...40%) описує дослідні дані отримані в умовах вакууму. З рішення системи рівнянь 
і Rв = 0,4gτв2 відносно Rв і
τв виходить, що
(19.7)
(19.8)
Звідси виходить, що відривний діаметр одиничної бульбашки dв у динамічному режимі відриву обумовлюється (через сталу росту β) перегрівом поверхні теплообміну.
Найбільш загальний варіант схеми визначення відривних характеристик бульбашок відрізняється від розглянутого додатковим урахуванням сил поверхневого натягу і в’язкості. Час контакту бульбашки з поверхнею нагріву розбивається на дві стадії: перша – від моменту виникнення до початку відокремлення від поверхні, друга – стадія відокремлення до моменту відриву. Приймається, що координату центру мас бульбашки у момент відриву можна визначити з емпіричної залежності s(τв) = 1,5Rв. Вважається, що на першій стадії сили, діючі на парову бульбашку спрямовані до стінки, більші сили намагаються відірвати її, а умовою переходу першої стадії до другої є рівновага сил
Fg = FR + Fν + Fσ, (19.9)
де Fg – підйомна архімедова сила, Fg = 4/3[πR3g(ρ –
ρn)]; FR – інерційна реакція рідини при рості бульбашки на стінці. Вважаючи, що бульбашка на протязі всього періоду росту зберігає сферичну форму s(τ) = R(τ), і що значення п у співвідношенні постійне і рівне 0,5, отримаємо:
(19.10)
За цих же умов сила тертя викликана в’язкістю буде:
Fν = 10πμβ2, (19.11)
а сила зчеплення, обумовлена поверхневим натягом
Fσ = 2πRcσ, (19.12)
де Rc – наближене значення найбільш сприятливого радіуса впадини – центра пароутворення, що визначається за формулою (17.49) без коефіцієнта С2.
Після знаходження значень R і τ у момент початку відокремлення бульбашки розв’язується друга частина задачі – визначаються відривні характеристики. Для цього використовується рівняння руху центра мас бульбашки, отримане з балансу сил, аналогічне (19.9).
Сили інерційної реакції рідини і в’язкого опору визначаються як для вільно спливаючої бульбашки, але при цьому вважається, що бульбашка на цій стадії з’єднана з поверхнею нагріву “ніжкою”. Сила поверхневого натягу на другій стадії не враховується. У цьому випадку рівняння руху центра мас набуває виду:
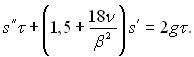(19.13)
Початковими умовами при вирішенні (19.13) служать отримані раніше значення R і τ у момент переходу від першої стадії до другої. Далі за умови s(τв) = 1,5Rв знаходяться відривні характеристики, які мають наступний вид:
(19.14)
(19.15)
де
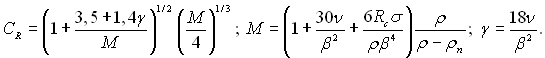
У цих виразах
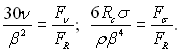(19.16)
З рівняння (19.14) витікають такі окремі випадки: а) співвідношення практично співпадає з (19.7) для динамічного режиму при FR >> Fσ; FR >> Fν; CR = 1,34; б) співвідношення для відривного розміру бульбашки при її відриві від кромки впадини – центра пароутворення у квазістатичному режимі:
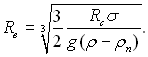(19.17)
Область коректного застосування формули (19.17) у квазістаціонарних умовах визначається співвідношенням між розміром Rc і капілярною сталою.
Для визначення частоти відриву бульбашок f = 1/ (τ1 +
τ2) у загальному випадку необхідно знати складові повного періоду
τ – час росту до відриву
τ1 і час очікування
τ2. Якщо відомі закон росту бульбашок і співвідношення для відривного розміру, то величину
τ1 можна отримати з рівняння росту бульбашки. Час виражається через поточний радіус, замість якого підставляється співвідношення для відривного радіуса. Внаслідок цього отримується співвідношення типу (19.15), яке виражає
τ1 через сталу росту
β у рівнянні 
Конкретний вид цих співвідношень визначається видом прийнятої залежності
τ від Ja.
Способи визначення τ2 розрізняються між собою. Одні дослідники пропонують вираз отриманий з рішення задачі про прогрів наполовину обмеженого масиву рідини при сталому прогріві її поверхні, внаслідок чого пропонується залежність:
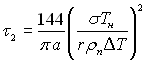. (19.18)
Інші τ2 знаходять з рішення задачі про прогрів наполовину обмеженого масиву рідини до заданого значення ΔТ на його поверхні при постійній густині підведеного теплового потоку q:
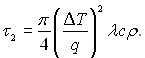(19.19)
Вирази (19.18) і (19.19) за своєю структурою різко відрізняються, що обумовлено різними вихідними посиланнями. Мабуть, обидва рішення далекі від дійсної залежності τ2 від режимних параметрів. Вираз (19.19) кращий в тому відношенні, що (19.18) відноситься тільки до центрів з оптимальною геометрією, тоді як (19.19) такого обмеження не має. Але у (19.19) не враховуються багато особливостей проходження процесу поновлення умов для зародження нової бульбашки на даному центрі, у тому числі – активації нових сусідніх центрів зі збільшенням густини теплового потоку.
Існує і інший підхід для знаходження часу τ2, який ґрунтується на тому, що після відриву бульбашки у пору – центр пароутворення – проникає рідина на певну глибину, яка залежить від кута змочування і діаметра пори. За рахунок теплоти, яка підводиться від поверхні нагріву в околицю центра пароутворення, відбувається випаровування рідини у порі з поверхні меніска і виштовхування її з пори. Період очікування τ2 визначався як час, необхідний для повного витіснення рідини парою, яка утворюється при заданому перегріві поверхні ΔТс. Час контакту бульбашки з поверхнею нагріву τ1 визначався звичайним способом за співвідношенням для росту бульбашки R(τ) і відривного розміру Rв. Отримані залежності f(ΔТс) мають асимптотичний характер: зі збільшенням ΔТс із-за скорочення часу τ2 значення f швидко збільшується і наближається до певної границі, яка відповідає величині τ1.
Отримані розрахункові дані для води і метанолу у графічному вигляді залежності частоти утворення бульбашок від перегріву поверхні для пор різних діаметрів наведено на рис.19.5, штриховою лінією показані дослідні дані осереднених значень f, отриманих для ансамблю бульбашок при кипінні води. Як видно, розрахункові і дослідні значення f знаходяться досить близько. Але можливості і точність запропонованого розрахункового методу не варто перебільшувати, тому що в дослідах час очікування τ, тоді як хороше спів падіння дослідних і розрахункових даних спостерігається у тому інтервалі ΔТс, де розрахунковий час очікування τ2 близький до нуля.
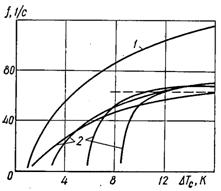
Рис.19.5. Залежність частоти утворення бульбашок від перегріву поверхні для метанолу (Rc = 2,5 мкм) (1) і води (Rc = 25,4...4,4 мкм) (2)
Розбіжність між розрахунковими і дослідними значеннями τ2 пояснюються рядом причин: 1) геометрична форма реальних пор значно відрізняється від ідеалізованої форми, яка прийнята у розрахункових схемах; 2) методи, які основані на використанні величини крайових кутів, не можуть претендувати на велику точність.
Наближена оцінка частоти утворення бульбашок трохи полегшується, якщо τ2 → 0. Це область високих тисків і високих густин теплового потоку. У цьому випадку значення частоти близька до f = 1/τ1. При низьких тисках і малих густинах теплового потоку значення частоти наближається до f = 1/τ2. Між цими крайніми випадками знаходиться досить широка область параметрів, у якій помітним чином впливають на f обидві складові (τ1 і τ2) повного часу.
Розрахункове визначення внутрішніх характеристик процесу кипіння представляє собою складну задачу навіть для ідеалізованих умов роботи одиничного центру пароутворення. Запропоновані рішення для відривних діаметрів і частот основані на спрощеній уяві, яка далека від дійсності. Діючі на бульбашку сили розраховуються зазвичай тільки наближено, а деяких випадках і некоректно. Так підйомна архімедова сила знаходиться зі спрощеного виразу 
без урахування розміру основи бульбашки. Якщо врахувати надлишковий тиск пари у бульбашці і прийняти, що основа бульбашки має форму круга з діаметром dк, то
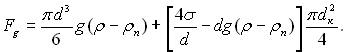(19.20)
Вираз для сили зчеплення, обумовлений поверхневим натягом, записується також спрощено. У загальному виді
(19.21)
зазвичай приймають f(θ) = sin θ, θ = 90°, Fσ = πdкσ.
Ще більше невизначеності і довільного тлумачення у підході до визначення сили опору Fν, обумовленою в’язкістю рідини.
Недостатньо повно і коректно оцінюється ефект дії інерційної реакції рідини FR. Навіть у кращих варіантах розв’язку задачі про відривний діаметр показник степеня п у виразі 
приймається постійним і рівним 0,5. Між іншим при кипінні на поверхні нагріву цей показник змінюється у часі: з ростом бульбашки помітно зменшується, досягаючи мінімуму перед відривом бульбашки. При суттєвому сповільненні росту бульбашки з відповідним зменшенням п до значень, менших 0,25, змінюється знак інерційної сили, і вона з сили притискування перетворюється на відривну. У той же час у рівнянні балансу сил внаслідок прийняття п = const = 0,5, сила інерції FR завжди ураховується як сила притискування. Цей суттєвий недолік пояснюється відсутністю надійних дослідних даних про зміну п під час росту бульбашки в різних умовах кипіння і труднощами розв’язку задачі при постановці її в загальному виді.
Методи теоретичного визначення частоти відриву бульбашки розвинені ще в меншому ступені, ніж методи знаходження відривного розміру парового утворення.
