20.4. Вплив властивостей поверхні нагріву на теплообмін при кипінні

Вплив умов поверхні на процес кипіння визначається у загальному випадку фізико-хімічними властивостями поверхні нагріву і взаємодією між твердою стінкою, рідиною і парою (змочування, адгезія, адсорбція), мікрогеометрією поверхні (розміри і форми тріщин і пор) і теплофізичними властивостями матеріалу поверхні нагріву (теплопровідність, коефіцієнт теплозасвоєння). Усі ці фактори впливають одночасно і до певної міри зв’язані між собою. Отже для вирішення проблеми у комплексній постановці перерахованих даних ще недостатньо. Тому приходиться розглядати у першому наближенні окремі частини проблеми – ізольований вплив тих чи інших факторів чи груп суміжних факторів.

Найменш відоме питання про роль фізико-хімічних факторів. Показники деяких з них важко піддаються кількісній оцінці і сильно залежать від ступені чистоти поверхні (відсутність забруднень і оксидних плівок), способу обробки і припрацювання, залишкових механічних напружень та ін. Не дивлячись на наявність ряду дослідних робіт, кількісна оцінка впливу цієї групи факторів на інтенсивність теплообміну поки що неможлива. Їх сумарний вплив мабуть незначний, тому що неврахування їх не викликає при опрацюванні дослідних даних по a при кипінні.

У кращому стані знаходиться справа з оцінкою впливу мікрогеометрії поверхні нагріву. Основною характеристикою структури поверхні є її шорсткість – сукупність нерівностей, які утворюють рельєф поверхні. ГОСТ 2.309–73 установлює 14 класів шорсткості чи чистоти поверхні. Класи чистоти визначаються числовими значеннями середньоарифметичного відхилення профілю за висотою нерівностей профілю по десяти точкам при нормованих базових лініях. При цьому на поверхні можуть бути впадини і виступи шорсткості любих розмірів до обмежень передбачених класом чистоти.

У відповідності з існуючими уявленнями стійкими центрами пароутворення можуть бути тільки ті елементи мікрорельєфу поверхні, які не заповнюються рідиною після відриву парової бульбашки. Поряд зі змочуванням поверхні основними факторами, які визначають спроможність впадини зберігати готовий паровий зародок, є її форма і розмір. Впадини достатньо великого розміру, заповнені рідиною, активними центрами не можуть бути.

Таким чином, ступінь чистоти обробки поверхні може впливати на інтенсивність теплообміну тільки тоді, коли її зміна супроводжується появою нових центрів пароутворення – розширенням спектру активних впадин. Якщо при зміні чистоти поверхні утворюються крупні впадини, які заповнюються рідиною, то така зміна не впливає на інтенсивність теплообміну.

Такий висновок підтверджується конкретними результатами дослідів про вплив шорсткості на інтенсивність теплообміну при кипінні. Далі розглянемо дослідні дані отримані при кипінні таких рідин, як вода і гелій (знаходяться на різних полюсах відносно р_кр, сильно відрізняються значеннями крайових кутів q та ін.).

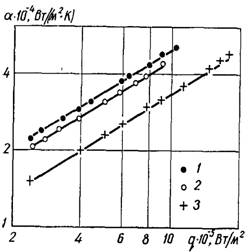
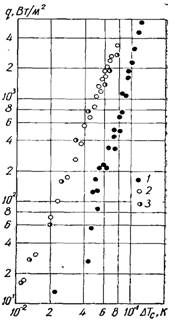
­Рис.20.7. Вплив чистоти обробки поверхні нагріву на інтенсивність

тепловіддачі при кипінні води з недогрівом (р = 0,4 МПа; DТ_нед = 20 К; матеріал поверхні – Х18Н9Т): 1 – холоднотягнуті трубки; 2 – точені трубки; 3 – поліровані трубки

Рис.20.8. Залежність інтенсивності тепловіддачі від шорсткості поверхні нагріву при кипінні гелію (р = 0,1 МПа) при R_z: 1 – 1 мкм; 2 – 5 мкм; 3 – 10 мкм­

Досліди при кипінні води з недогрівом до 20 К виконані на вертикальних трубках з нержавіючої сталі Х18Н9Т, а при кипінні гелію – на горизонтально розташованому торці мідного стрижня (рис.20.7 і 20.8). З рисунків видно, що в обох дослідах отримано співпадаючі в принциповому відношенні результати, з яких слідує важливий висновок. По мірі збільшення шорсткості, починаючи з гладкої полірованої поверхні, інтенсивність теплообміну збільшується і досягає певного граничного значення (при класі чистоти до 8). Після чого подальше збільшення шорсткості поверхні вже не впливає на інтенсивність теплообміну. До того ж при тривалій роботі у ході самого процесу кипіння відбувається “дообробка” поверхні нагріву, внаслідок якої згладжуються початкова різниця в стані різних поверхонь. Отже, для технічних поверхонь нагріву вплив шорсткості на інтенсивність теплообміну можна не враховувати.

Вплив теплофізичних властивостей матеріалу поверхні тепловіддачі обумовлений просторовою дискретністю і локальною не стаціонарністю процесу, які супроводять кипіння на твердій поверхні. Тому розгляд питання про вплив теплофізичних властивостей твердої стінки можливий у двох аспектах. Перший з них пов’язаний з просторовою дискретністю центрів пароутворення, другий – з не стаціонарністю теплообміну між поверхнею нагріву і рідиною біля центрів пароутворення.

Центри пароутворення є місцями інтенсивного стоку теплоти з густиною теплового потоку, яка значно перевищує середню по поверхні. Внаслідок цього осереднена температура біля діючого центра пароутворення в поверхневому шарі поверхні тепловіддачі нижче, ніж на решті вільної поверхні. При цьому, із-за перерозподілу теплового потоку відбувається зменшення температури вільної поверхні в порівнянні з температурою, необхідною для реалізації середнього по поверхні теплового потоку при відсутності кипіння.

Наявність діючих центрів пароутворення зменшує поверхневу температуру не тільки біля центра, а і на вільній поверхні, що відображається на підвищенні середньої інтенсивності теплообміну. Природно, що чим вища теплопровідність матеріалу стінки, тим більш інтенсивно буде відбуватися перерозподіл теплових потоків між частинами вільної поверхні і поверхні, що зайнята активними центрами пароутворення. З цього можна зробити загальний висновок про вплив теплопровідності матеріалу на інтенсивність теплообміну при бульбашковому кипінні. Але він справедливий тільки для поверхонь, які бідні потенціальними центрами пароутворення. У випадку шорсткої поверхні, яка має достатньо велику кількість потенціальних центрів пароутворення, теплопровідність твердої стінки не може робити суттєвий вплив на інтенсивність теплообміну.

При низькій теплопровідності стінки перерозподіл локальних теплових потоків між вільною поверхнею і поверхнею, яка зайнята активними центрами, буде затруджений. Зі збільшенням загального теплового потоку збільшується температура вільної поверхні. Це приводить до активації потенціальних центрів на вільній поверхні і до зменшення її температури, тобто до підвищення інтенсивності теплообміну. Тому можна чекати, що при низькій теплопровідності стінки тепловий потік, який реалізується кожним одиничним центром, менше, ніж у поверхні з високою теплопровідністю, на якій число активних центрів пароутворення більше. Таке уявлення відповідає даним, отриманим при дослідженні внутрішніх характеристик при кипінні води і етанолу на поверхнях нагріву виконаних з різних матеріалів.

При кипінні на гладких поверхнях (з дуже обмеженою кількістю потенціальних центрів пароутворення) збільшення теплового потоку не супроводжується виникненням достатньої кількості додаткових центрів пароутворення, і при низькій теплопровідності стінки середня по поверхні температура збільшується, тобто інтенсивність теплообміну зменшується. Це підтверджується дослідними даними, отриманими при кипінні етанолу і бензолу на полірованих трубках з срібла, нікелю і нержавіючої сталі. Висока чистота обробки поверхні призвела до зменшення кількості можливих центрів пароутворення, що обумовило зменшення інтенсивності теплообміну. Однак найбільший інтерес представляє те, що інтенсивність тепловіддачі при кипінні бензолу на срібних трубках була значно вищою, ніж на трубках з нержавіючої сталі. Локальний перерозподіл теплових потоків при високій теплопровідності срібла у порівнянні з нержавіючою сталлю компенсувало зменшення кількості активних центрів пароутворення із-за високої чистоти обробки.

При кипінні криогенних рідин теплопровідність матеріалу поверхні нагріву оказує вплив на інтенсивність теплообміну навіть при помірному ступені чистоти (5...7 клас). Криогенні рідини дуже добре змочують поверхні нагріву, їх крайовий кут близький до нуля. Внаслідок цього при звичайній обробці поверхні на ній не утворюється достатньої кількості впадин, які могли б бути потенціальними центрами пароутворення. Шорстка поверхня для звичайних рідин, для криогенних оказується гладкою. Тільки спеціальною обробкою, при якій створюється мікропористий поверхневий шар, удається отримати поверхню достатньо шорстку для криогенних рідин.

Таким чином, з розгляду питання в першому аспекті виходить, що теплопровідність матеріалу стінки може оказати помітний вплив на інтенсивність теплообміну при бульбашковому кипінні тільки у випадку обмеженої кількості потенціальних центрів пароутворення на поверхні нагріву.

Питання про вплив теплофізичних властивостей матеріалу поверхні нагріву в другому аспекті – у зв'язку з не стаціонарністю процесу теплообміну між твердою стінкою і рідиною – розглядувався багатьма дослідниками. У наслідок чого було виявлено, що інтенсивність теплообміну при кипінні залежить від коефіцієнта теплозасвоєння (акумуляції) А= (lсr)^0,5 матеріалу поверхні тепловіддачі, що знайшло своє кількісне підтвердження у випадку кипіння криогенних рідин.

Стосовно звичайних рідин, то наявні дослідні дані свідчать про те, що при кипінні їх на технічних поверхнях нагріву вплив матеріалу стінки незначний. Так при кипінні етанолу в коридорній системі підігрівачів коефіцієнти тепловіддачі у крайніх випадках (при кипінні на мідній і поверхні з нержавіючої сталі) при q = idem, відрізняються приблизно на 20%, тобто змінюється в межах ±10% від середнього значення. При цьому необхідно мати на увазі, що у випадку кипіння звичайних рідин виділити вплив теплофізичних властивостей поверхні нагріву дуже важко. Для криогенних же рідин при q = idem максимальне значення a (на мідній поверхні) може бути більше мінімального значення (на поверхні з нержавіючої сталі) у декілька разів. Це пояснюється тим, що при охолодженні до криогенних температур, особливо до гелійових, сильно і різним чином для різних металів змінюються (погіршуються) їх теплофізичні властивості. Різко зменшується коефіцієнт тепло засвоєння (lсr)^0,5 нержавіючої сталі і при температурі 4,2 К його абсолютна величина дуже мала 33...42 Вт·с^1/2/(м²·К).

На підставі сказаного, можна зробити загальний висновок про вплив на a властивостей поверхні нагріву, що у межах наближеного (досі єдино можливого) рішення задачі з визначення a при кипінні цей вплив для звичайних рідин можна не ураховувати, а враховувати його необхідно тільки у випадку кипіння криогенних рідин, особливо – гелію.

20.5. Інтенсивність теплообміну при кипінні у великому об’ємі. Розрахункові рівняння

На сьогоднішній день існує велика кількість різних формул для визначення коефіцієнта тепловіддачі a при розвиненому бульбашковому кипінні насиченої рідини за умови вільної конвекції. У більшості випадків це емпіричні формули типу:

a = cqⁿf(p), (20.1)

які узагальнюють дослідні дані одного чи іншого автора у досліджуваному інтервалі зміни режимних параметрів. Значення коефіцієнта с і показника степеня п, а також вид функції f(p) у цих формулах залежать від багатьох факторів, які чинять вплив на інтенсивність теплообміну кипінні (діапазону зміни р і q, стану і фізико-хімічних властивостей поверхні нагріву та ін.)

Формули типу (20.1) зазвичай застосовують для розрахунку інтенсивності теплообміну при кипінні тих рідин, для яких у довідковій літературі відсутні дані про теплофізичні і термодинамічні властивості, чи для рідин, в характері процесу кипіння яких спостерігаються специфічні особливості. Наприклад, у літературі відсутні повні дані про властивості деяких фреонів. Візуальні спостереження і кінозйомка показують, що при кипінні фреонів діаметр парових бульбашок при відриві від поверхні теплообміну порядок менші відривного діаметра бульбашок при кипінні води у відповідних умовах. Частота пароутворення при кипінні фреонів також більша, ніж при кипінні інших рідин. Тому для розрахунку коефіцієнта тепловіддачі при розвиненому бульбашковому кипінні фреонів на поверхні одиничних труб запропонована залежність

a = cqⁿf(p), (20.2)

де коефіцієнт с визначається через параметри речовини у критичному стані (р_кр і Т_кр) і її молекулярну масу М по формулі

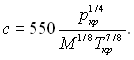
Для деяких фреонів значення с наведені у табл.20.1

     Таблиця 20.1

Значення функції f(p) залежить від інтервалу тисків. Для інтервалу зміни тиску 0,02 < р/р_кр < 0,06 функція f(p) має вид

f(p) =0,18 + 1,53(р/р_кр). (20.3)

В діапазоні зміни тиску 0,06 < р/р_кр < 0,5

f(p) =0,14 + 2,2(р/р_кр). (20.4)

Як видно із співставлення формул (20.3) і (20.4), при більш високих тисках вплив р більш різкий. Формула (20.2) з точністю ±20% узагальнює багато чисельні дослідні дані, отримані різними авторами при кипінні фреонів в широкому діапазоні зміни режимних параметрів.

Точка зору С.С.Кутателадзе криється в тому, що при аналізі теплообміну в процесі кипіння необхідно явища, які відбуваються в рідкій фазі, розглядати окремо від явищ у паровій фазі. При цьому вважається, що передача теплоти від поверхні нагріву при бульбашковому кипінні може здійснюватися як до рідкої, так і до парової фази. У той же час ефект переносу теплоти до рідини значно перевищує інтенсивність передачі теплоти до пари (із-за малої теплопровідності пари). Тому теплота тратиться на перегрів рідини, яка далі випаровується у парові бульбашки.

Процес теплообміну і руху для одиничної бульбашки заданого розміру пропонується описати системою рівнянь, до якої входять:

рівняння теплопровідності у рідкій фазі

(20.5)

рівняння руху і суцільності рідкої фази

(20.6)

рівняння руху і суцільності парової фази

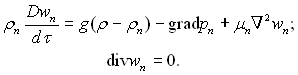(20.7)

Умови теплової взаємодії на границі розділу фаз:

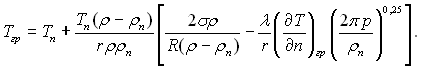(20.8)

Умови механічної взаємодії на границі розділу фаз:

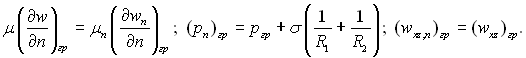(20.9)

Замикаючим прийнятий масштаб сформованих бульбашок і розподіл центрів пароутворення по поверхні теплопередачі

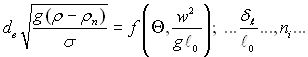(20.10)

Ця система рівнянь дає можливість отримати ті числа подібності, за допомогою яких на підставі дослідних даних Кутателадзе запропонував розрахункову залежність

(20.11)

де

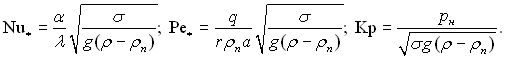
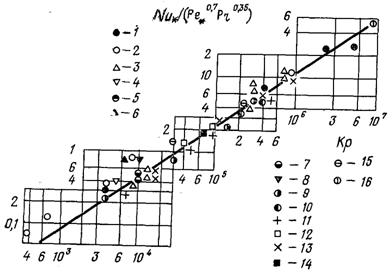
Рис.20.9. Співставлення дослідних даних при кипінні у великому об’ємі з узагальнюючою залежністю (20.11): 1 – вода 0,098...17,85 МПа; 2 – вода 0,011...0,1 МПа;3 – метан р = 0,102...2,32 МПа;4 – чотирихлористий вуглець 0,098 МПа;5 – ізопропілен 0,098 МПа; 6 – метанол 0,098 МПа; 7 – п-бутанол 0,098 МПа; 8 – азот 0,098 МПа; 9 – п-гентан 0,0465...1,47МПа; 10 – п-пропан 1,17 і 1,69 МПа; 11 – бензол 0,101...1,86МПа; 12 – етанол 0,101...0,785 МПа; 13 – п-пентан 0,147 і 0,795 МПа;14 – аміак t_н = 15...19 °С; 15 – етанол 0,294...3,36 МПа; 16 – вода 19,6 МПа

На рис.20.9 співставленні дослідні значення a, отримані при кипінні багатьох рідин з розрахунковою залежністю (20.11). З рисунка видно, що ця формула задовільно погоджується з багатьма дослідними даними. Але вона не узагальнює деякі дослідні дані, отримані при кипінні фреонів. У ряді робіт показано, що для цієї групи рідин дослідні дані для a у деяких випадках суттєво вище величин визначених по формулі (20.11).

Формула, яка узагальнює як дані, використані при побудові залежності (20.11), так і ряд інших даних, включаючи фреони, отримана М.Г.Стюшіним. Ця формула має вид

(20.12)

де

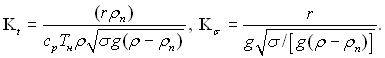
Співставлення дослідних даних з формулою (20.12) наведено на рис.20.10 і 20.11, з яких видно що для більшості рідин дослідні значення a відхиляються від розрахункової залежності не більш як на ±20%.

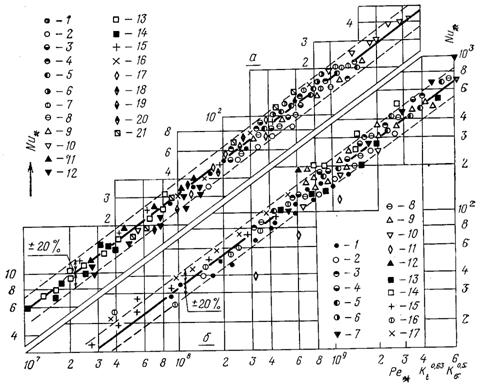
Рис.20.10.Співставлення дослідних значень a при кипінні у великому об’ємі з узагальнюючою залежністю (20.12): а) 1...7 – вода 0,098, 0,587, 2,25, 5,48, 9,8, 14,7,17,8 МПа; 8...10 – вода 0,451, 0,98,19,6 МПа; 11 – метанол 0,098 МПа;12 – п-бутанол 0,098 МПа; 13 – ізопропанол 0,098 МПа; 14 – чотирихлористий вуглець 0,098 МПа; 15 – азот 0,098 МПа; 16...20 – вода 0,1, 0,05, 0,03, 0,02, 0,011 МПа; 21 – дифеніл 0,252 МПа; б) 1 – 1...10 – етанол 0,098, 0,3, 0,5, 0,686, 0,98, 1,94, 2,94, 3,95, 4,9, 5,29 МПа; 11...14 – етанол 0,294, 0,98, 1,96, 3,36 МПа; 15...17 – бензол 0,101, 0,245, 0,353 МПа

З графіків виходить, що при значеннях комплексу А = 3,2·10^–5, а п = 0,75.

У випадках при N = 10^–7 для поверхонь теплообміну, які спеціально не оброблялися, спостерігається перехід від режимів, в яких ще проявляється конвективний перенос маси і теплоти, до режимів, коли інтенсивність теплообміну обумовлена виключно процесом пароутворення. Для більш гладких поверхонь перехідне значення N трохи більше, а для шорстких – менше. Однак у всіх випадках за перехідним значенням N коефіцієнти А і п мають наведені вище значення.

За умови 5·10⁵ < N < 10⁷, А = 2,65·10^–2, а п = 1/3 – у режимах, які установилися при зменшенні теплового потоку. Коли дослід проводиться з підвищенням теплового потоку, то внаслідок явища гістерезису залежність a від q проходить більш полого (п = 0,25).

При значеннях N < 10⁷ на механізм теплопереносу, викликаний процесом кипіння, накладається вплив механізму переносу природною конвекцією середовищ. У цій області спостерігається суттєво менший вплив тиску, а сам процес теплообміну характеризується меншою стійкістю, тому у цій області спостерігається великий розкид дослідних точок.

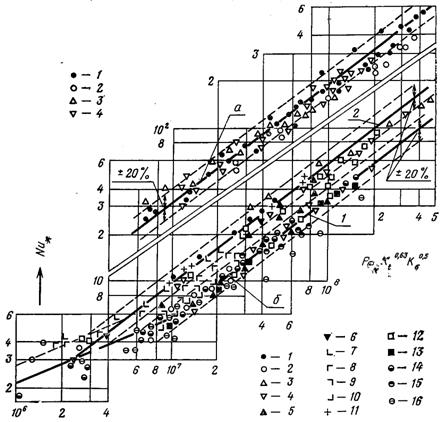
Рис.20.11. Співставлення дослідних значень a при кипінні у великому об’ємі алкінів (а), фреонів і аміаку (б) з узагальнюючою залежністю (20.12): а) 1 – метан 0,102, 0,231,0,928, 1,39, 2,32, 2,79 МПа; 2 – п-пентан 1,17, 1,69, 2,59 МПа; 3 – п-гептан0,0455,0,101, 0,309 МПа; 4 – п-пентан 0,412, 0,795, 1,47, 2,18, 2,86 МПа; б) Ф-12: t_н = 15...19°С; 2 – t_н = –15°С; 3 – t_н = 16...19°С; 4 – t_н = –10...+20°С; Ф-21: 5 – t_н = 50°С; Ф-22:6 – t_н = 23°С; 7 – р/р_кр = 0,093; 8 – р/р_кр = 0,072; 9 – р/р_кр = 0,05; 10 – р/р_кр = 0,022; 11 – t_н = 16...20°С; 12 –t_н = –10...+20°С; Ф-113: 13 – t_н = 47°С; Ф-142: 14 – t_н = –10...+20°С; аміак: 15 – t_н = 15...19°С; 16 – t_н = –40...+20°С;

На рис.20.11 (крива б) нанесені дослідні дані отримані при кипінні фреонів. На цьому графіку крива 1 відповідає залежності (20.12). Усі дослідні дані для фреонів Ф-12, Ф-21, Ф-22, Ф-113 і Ф-142 при тисках менших чи рівних 0,06 р_кр, розташовуються біля розрахункової кривої з розкидуванням точок, в основному не більшим ±20%. Біля кривої 2 розташовуються дослідні точки, отримані при кипінні тих же фреонів в інтервалі тиску від 0,1р_кр до 0,5р_кр. Для цієї кривої в області розвиненого бульбашкового кипіння коефіцієнт А у формулі (20.12) на 60% більший, ніж для основної залежності, і становить 5,1·10^–5.

В інтервалі тиску (0,06...0,1)р_кр при розрахунку коефіцієнту А у формулі (20.12) допускається лінійна інтерполяція між його крайніми значеннями, яка відповідає лініям 1 і 2. З графіка видно, що при р/р_кр = 0,093 дослідні точки лежать на кривій 2, при р/р_кр = 0,05 – на кривій 1, а при р/р_кр = 0,072 – між лініями 1 і 2.

Число Кs, яке входить у формулу (20.12) для кожної рідини має приблизно постійне значення у широкому діапазоні зміни тиску. У табл.20.2 наведені значення числа Кs·10^–7 для деяких рідин при різних тисках.

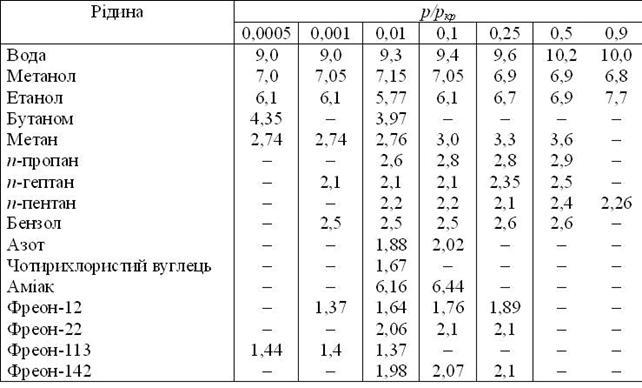
На підставі аналізу механізму кипіння В.І.Толубінським прийнята наступна система безрозмірних величин:

Nu = Nu(Pe, Fo, Pr,  ℓ_*, r_*), (20.13)

де

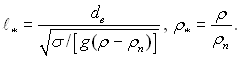
Представимо цю залежність для визначення інтервалу значень у вигляді степеневої функції:

(20.14)

Рівняння подібності (20.14) можна представити у наступній формі:

(20.15)

де т₂ = п₂ – т₁, а число подібності

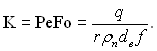(20.16)

Комплекс К в аналогічній формі був запропонований Якобом, виходячи з інших міркувань. Він не розглядав добуток d_вf як середню швидкість росту бульбашок wІ і вважав d_вf величиною сталою і однаковою для всіх рідин.

Показники степені і стала в рівняннях подібності визначаються на підставі дослідних даних. Внаслідок опрацювання і співставлення даних по a при кипінні для різних рідин в широкому діапазоні зміни тиску і теплового навантаження оказалося, що показник т₄ недалекий від одиниці, а т₅ – до нуля. Це дозволяє спростити рівняння подібності

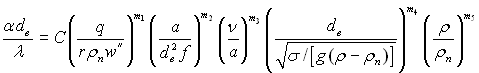(20.17)

і привести його до виду

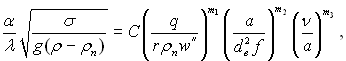(20.18)

чи у скороченій формі запису

(20.19)

[тут і в подальшому для системи вибраної В.І.Толубінським використовується число Нуссельта представлене у рівнянні (20.18)].

Крім того, оказалося, що показники п₂ і т₁ відрізняються один від іншого незначно (т₂ = п₂ – т₁ » 0,1) і тому рівняння подібності можна подати у гранично простій формі:

Nu = CK^mPrⁿ. (20.20)

У відповідності з (20.20) і накопиченим дослідним матеріалом цю залежність можна подати в конкретному вигляді узагальнюючою залежністю – розрахункового рівняння для визначення інтенсивності теплообміну (коефіцієнта тепловіддачі a) при бульбашковому кипінні:

Nu = 75K^0,7Pr^–0,2, (20.21)

чи у розгорненій формі запису

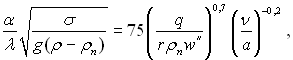(20.22)

де wІ – середня швидкість росту парових бульбашок, м/с; a – коефіцієнт тепловіддачі при кипінні, Вт/(м²·К); r_п – густина пари, кг/м³ (усі фізичні властивості рідини і пари – на лінії насичення).

Для визначення осередненої залежності для wІ у випадку відсутності дослідних значень цієї величини, можна у першому задовільному наближенні використовувати дані наведені на рис.20.12. Залежність наведена на цьому рисунку охоплює широкий діапазон П = р_кр/р від 1,1 до 250. Також у широкому інтервалі П від 2,5 до 100 для визначення wІ, м/с, можна користуватися емпіричними залежностями

wІ = 3,6·10^–4П^1,4, (20.23)

чи

wІ = 3,6·10^{–4p –1,4}, (20.24)

де p = р/р_кр.

Формулу (20.24) можна розглядати, як частинний і наближений вид співвідношення wІ/(аg)^1/3 = Ф(р/р_кр) між безрозмірною швидкістю росту парових бульбашок і приведеним тиском у тому інтервалі значень p, де цю залежність можна апроксимувати степеневою функцією.

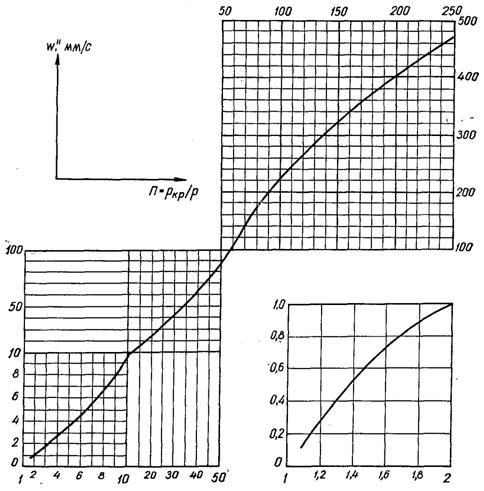
Рис.20.12. Осереднена залежність середньої швидкості росту парової бульбашки wІ від П

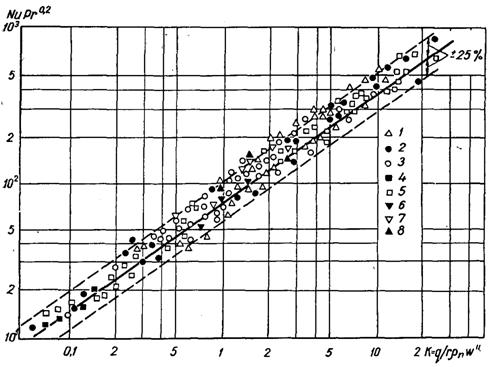
Рис.20.13. Узагальнення дослідних даних при кипінні спиртів – етанолу (1...5), метанолу (6, 7) і бутанолу (8) при тисках, МПа: 1 – 0,3...0,98; 2 – 0,1...2,3; 3 – 0,1; 4 – 0,1; 5 – 0,1...3; 6 – 0,1; 7 – 0,1; 8 – 0,1 [суцільна лінія – розрахункові значення по (20.21)]

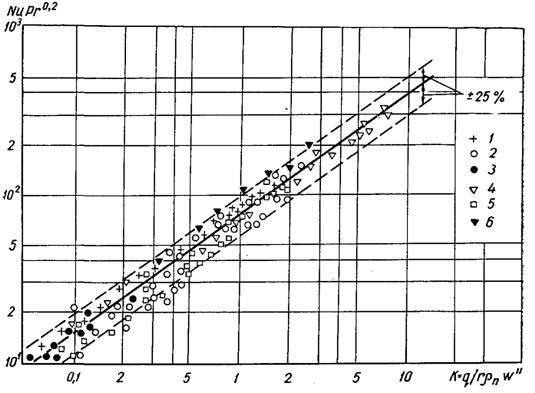
Рис.20.14.Узагальнення дослідних даних при кипінні фреонів – Ф-11 (1), Ф-12 (2...4), Ф-22 (5, 6) при тисках, МПа:1 – 0,1; 2 – 0,151...1,5; 3 – 0,2...0,35; 4 – 0,6...2,3; 5 – 0,124...2,44; 6 – 0,83...2,0 [суцільна лінія – розрахункові значення по (20.21)]

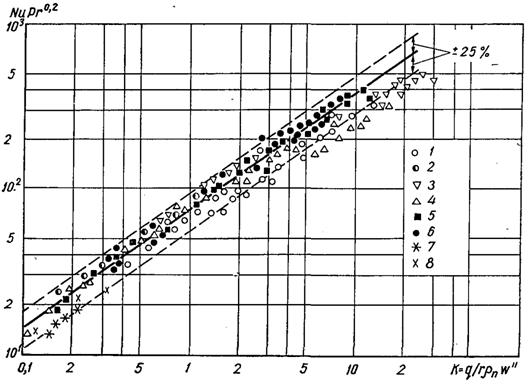
Рис.20.15. Узагальнення дослідних даних при кипінні важких вуглеводів – бензолу (1...5), пропану (6), чотири хлористого вуглецю (7, 8) при тисках, МПа: 1 – 0,1...3,6; 2 – 0,1; 3 – 0,79...4,55; 4 – 0,1...2,07; 5 – 0,1; 6 – 0,64...1,72; 7 – 0,1; 8 – 0,1 [суцільна лінія – розрахункові значення по (20.21)]

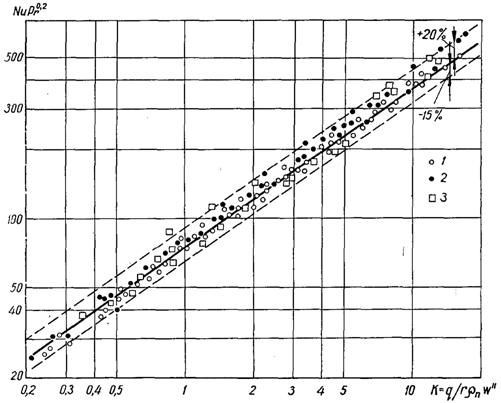
Рис.20.16.Узагальнення дослідних даних при кипінні легких вуглеводів – метану (1), етану (2), етилену (3) ) при тисках, МПа: 1 – 0,1...2,3; 2 – 0,127...2,94; 3 – 0,127...2,45 [суцільна лінія – розрахункові значення по (20.21)]

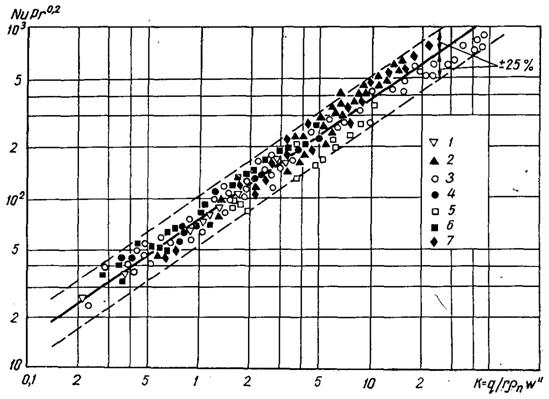
Рис.20.17. Узагальнення дослідних даних при кипінні води при тисках, МПа: 1 –0,1; 2 – 0,1...19,6; 3 – 0,1...16,9; 4 – 0,009...0,1; 5 – 0,1...7,0; 6 – 0,1...1,0; 7 – 0,1...1,97 [суцільна лінія – розрахункові значення по (20.21)]

Консерватизм закономірностей теплообміну при бульбашковому кипінні рідин підтверджується результатами узагальнення дослідних даних по інтенсивності теплообміну при кипінні. На рис.20.13...20.16 у системі узагальнених координат NuPr^0,2 = f(K) у відповідності з рівнянням (20.21) наведені узагальнені дослідні дані по a при кипінні різних органічних рідин (спиртів, фреонів і вуглеводних). При опрацюванні дослідних даних про a значення wІ для всіх рідин визначалися по кривій рис.20.12. В інтервалі П від 2,5 до 100 їх можна також розраховувати по співвідношенню (20.23). Як видно з рис.20.13...20.16 дослідні дані задовільно узагальнюються рівнянням (20.21) в широкому діапазоні тисків і густин теплового потоку, розкидання дослідних точок біля розрахункової лінії знаходиться у межах ±25%, тобто в області, характерній для звичайного розходження дослідних даних по a для однієї і тої ж рідини у різних дослідників.

На рис.20.17 у тій же координатній системі наведено узагальнення дослідних даних про a при кипінні насиченої води в інтервалі тиску від 0,009 до 19,6 МПа і густині теплового потоку від 0,02 до 3,5 МВт/м², а також дані про a при кипінні води з недогрівом при тисках від 0,1 до 1,0 МПа і недогрівах від 5 до 60 К.