Розділ 21. ОКРЕМІ ВИПАДКИ КИПІННЯ

21.1. Неізотермічні поверхні нагріву

Збільшення граничних густин теплового потоку, який відводиться від поверхні теплообміну без через мірного збільшення її температури, можна досягнути у багатьох випадках шляхом застосування ребристих поверхонь. Особливість умов теплообміну при кипінні на такій поверхні – неізотермічність поверхні теплообміну. Внаслідок кінцевої теплопровідності ребра на його поверхні установлюється температурне поле, яке характеризується зменшенням температури від основи ребра до його вершини. При високій густині теплового потоку, що перевищує q_кр для гладких без ребер стінок, біля основи ребра на прилеглій до нього гладкій поверхні виникає плівкове кипіння. У міру віддалення від основи ребра і зменшення температури спостерігається кипіння у перехідній області, а далі – бульбашкове кипіння. При достатній висоті ребра на його вершині може відбуватися однофазний теплообмін.

Тепловий розрахунок неізотермічної ребристої поверхні представляє великі труднощі. Це пояснюється тим, що на відмінність від розрахунку ребристої поверхні при однофазному теплообміні неможна застосовувати постійність величини коефіцієнта тепловіддачі за висотою ребра.

Оскільки методів, які дозволяють надійно розраховувати інтенсивність теплообміну при змішаному кипінні на неізотермічній поверхні не існує, то у першому наближенні використовується для визначення a по висоті ребра криві кипіння, отримані для ізотермічних умов. Але цей метод дає хороші результати при порівнянно низьких теплових потоках до (0,8...0,95)q_кр. При більш високих теплових навантаженнях (порядку (1,25...2,0)q_кр) ребриста стінка розсіює потужність на 15...30% вище розрахункової. Причиною цього є взаємодія різних форм кипіння, які сприяють інтенсифікації теплообміну на неізотермічні поверхні.

Дослідження кипіння на одиничному горизонтальному мідному ребрі із застосуванням швидкісної кінозйомки показали стійке співіснування на поверхні неізотермічного ребра різних режимів кипіння від плівкового до бульбашкового, які плавно переходять від одного до іншого. Над ділянками перехідного і плівкового кипіння спостерігаються інтенсивні висхідні токи, які затягують рідину із зони бульбашкового кипіння, створюючи спрямовану течію до основи ребра.

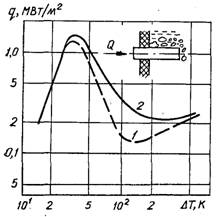
Рис.21.1. Локальна густина теплового потоку при кипінні води на ізотермічному (1) і неізотермічному (2) ребрах

Криві кипіння для локальних значень теплового потоку q_л і температурного напору DТ_л на неізотермічній поверхні мають стійку низхідну гілку (рис.21.1), а досягнуті граничні густини теплового потоку можуть трохи перевищувати q_кр для ізотермічної поверхні. На ділянці плівкового кипіння q_л слабко залежить від DТ_л, а в області бульбашкового кипіння криві для ізотермічної і неізотермічної поверхонь практично співпадають.

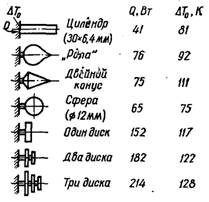
Рис.21.2. Типи одиничних мідних ребер рівного об’єму (950 мм3) і потужності, які ними реалізуються при кипінні фреону-113 у великому об’ємі

Для вибору оптимальної форми неізотермічного ребра виконано ряд досліджень. У результаті наближеного математичного аналізу знайдено, що оптимальне одиничне ребро повинно мати форму ріпи чи краплі (рис.21.2). Як показали випробування, таке ребро передає на 84% більше теплоти, ніж циліндричне ребро рівного об’єму. Недоліком такої форми є її не технологічність. Найкращим наближенням до ріпчастої форми оказалося ребро, яке складається з двох конусів, з’єднаних основами. Таке ребро реалізує майже такий тепловий потік, який характерний для ріпчастого ребра. Більш технологічними і, як показали досліди, навіть більш ефективними оказалося ребро у вигляді циліндричного диску на ніжці. Допустиме навантаження збільшується майже вдвічі у порівнянні з циліндричним ребром; при використанні трьох дисків воно збільшується до п’яти разів (див. рис.21.2).

Ребристі поверхні при кипінні оказалися перспективними і в іншому відношенні. Неізотермічність поверхні сприяє більш ранньому переходу від плівкового кипіння до бульбашкового при більш високих q_кр.2, ніж для гладкої поверхні, тому що бульбашкове кипіння, яке виникає на вершині ребра, інтенсивно охолоджує його і швидко розповсюджується до основи.

Це особливо важливо для криогенної техніки, тому що у цих пристроях спостерігається плівкове кипіння. Перехід до бульбашкового кипіння сприяє більш швидкому виходу пристроїв на робочі параметри.

21.2. Тепловіддача в пучках гладких і ребристих труб

Поверхні теплообміну ряду промислових випарників компонуються у вигляді горизонтального чи вертикального пучків труб, розміщених у кожусі. Занурена в об’єм рідини гріюча секція такого випарника утворює вільний циркуляційний контур з підйомним рухом парорідинної суміші у зоні пучка труб і з опускним рухом рідини біля кожуху. У такому контурі поверхня тепловіддачі обмивається потоком парорідинної суміші, яка створюється паровими бульбашками, що підіймаються вгору. Тому що паровміст, а значить і швидкість суміші збільшуються під час руху знизу вгору, то умови теплообміну для нижніх і верхніх рядів труб у горизонтальному пучці чи нижніх і верхніх елементів поверхні вертикальної секції, оказуються неоднаковими.

При високих теплових потоках вплив швидкості парорідинної суміші в умовах природної циркуляції практично не проявляється, тому в апаратах з високо форсованою поверхнею теплообміну значення коефіцієнта тепловіддачі на нижніх і верхніх трубах пучка практично однакове. При низьких теплових потоках (характерні режими для випарників) додаткова турбулізація пристінного шару, яка виникає при спрямованому русі середовища, може привести до суттєвого збільшення коефіцієнта тепловіддачі. Зрозуміло, що поняття “низький” чи “високий” тепловий потік необхідно розуміти як відносне.

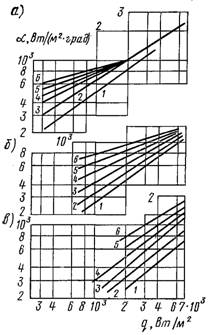
Рис.21.3. Залежність a від q при кипінні фреона-12 на поверхні труб шестирядного горизонтального пучка при t_н°С: а) 40; б) 10; в) –25; 1...6 – номера рядів труб у пучці знизу вгору

На рис.21.3 наведена залежність коефіцієнта тепловіддачі від густини теплового потоку при кипінні фреон-12 на окремих трубах шестирядного горизонтального пучка при різних температурах насичення (труби пронумеровані знизу вгору). З рисунка видно, що із збільшенням теплового потоку відносний коефіцієнт тепловіддачі для труби 6 і коефіцієнту тепловіддачі для труби 1 зменшується. Це значить, що із збільшенням теплового потоку вплив швидкості суміші слабшає. Більш значна залежність a від швидкості суміші спостерігається при низьких тисках. Це пояснюється тим, що при q =const зі зменшенням тиску збільшується швидкість суміші внаслідок підвищення питомого об’єму пари, яка утворюється на трубах. У той же час зменшенні тиску зменшується кількість активних центрів пароутворення і, як наслідок, зменшується частка теплоти, яка відводиться від стінки у вигляді теплоти випаровування.

За абсолютною величиною коефіцієнти тепловіддачі, отримані на одиничних трубах у пучці, практично однакові. Тільки при дуже низьких теплових потоках швидкість циркуляції чинить вплив на тепловіддачу від нижніх труб пучка.

Досліди показують, що після шостого ряду інтенсивність теплообміну стабілізується. Якщо кількість рядів у пучці більше десяти, то середнє значення a у пучці практично не залежить від кількості рядів і може визначатися множенням коефіцієнта тепловіддачі одиничної труби a_од на поправочний коефіцієнт e_п, який враховує інтенсифікацію теплообміну у пучці.

a_п = a_одeп. (21.1)

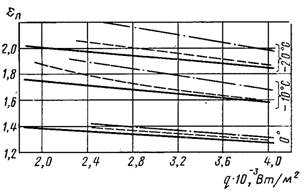
Рис.21.4. Залежність коефіцієнта e_п від теплового потоку, температури насичення і відносного кроку пучка s/d: ––– s/d = 1,45; -----s/d = 1,3;– ^. – ^.– s/d = 1,15

Коли значення комплексу N > 10⁷ у рівнянні (20.12), то поправочний коефіцієнт e_п = 1. За умови, що N < 10⁷ поправочний коефіцієнт e_п для фреонів визначається з рис.21.4. Наведена на цьому рисунку залежність e_п = f(q, t₀, s/d) отримана у дослідах на звичайних промислових трубах. Як бачимо, більш помітний вплив відносного кроку пучка s/d (відношення відстані між осями труб s до діаметра d) спостерігається при низьких температурах. При t₀ < –20°C рекомендується значення e_п приймати такі, як і при t₀ = –20°C.

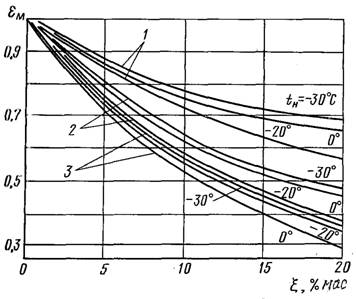
Рис.21.5. Залежність коефіцієнта e_м від концентрації масла у суміші x,, теплового потоку q і температури насичення t_н (фреон-22, одинична труба): 1 – q = 1,835 кВт/м²; 2 – q = 5 кВт/м²; 3 – q = 10 кВт/м²

Киплячий у промислових умовах фреон зазвичай містить у собі до 8...10% (масових) масла, що зменшує значення коефіцієнта тепловіддачі. Вплив домішки масла на інтенсивність теплообміну при кипінні фреонів можна урахувати додатковим коефіцієнтом e_м. На рис.21.5. наведені графіки, побудовані при кипінні Ф-22 з домішками масла ХФ-22С на одній трубі.

Якщо верхні ряди труб пучка обмиваються перегрітою на декілька градусів парою, то середні значення a_п пучка буде меншим, ніж при виході з випарника насиченої пари. Це значення може бути розраховане множенням коефіцієнта тепловіддачі, розрахованого без урахування поверхонь перегріву пари, на поправочний коефіцієнт e_пер, величина якого у залежності від ступеня перегріву Dt_пер визначається по формулі:

e_пер = 1 – 0,143Dt_пер. (21.2)

Вплив ребер на трубах. При кипінні рідини на ребристих поверхнях труб за умов малих значень теплового потоку установлюється більша інтенсивність теплообміну. Тому у випарниках низькотемпературних холодильних установок, які працюють за цих умов, широко використовують ребристі труби. Використовують труби з профілем ребер, наведених на рис.21.6. Труби відрізняються не тільки розмірами, а і коефіцієнтами ребер К_р = F_p/F_вн (F_p – зовнішня поверхня труби з урахуванням ребер, F_вн – внутрішня поверхня труби).

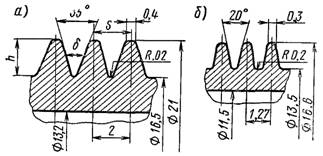
Рис.21.6. Профілі накатаних труб: а – К_р = 3,5; б – К_р = 4

Деякі результати отримані при кипінні Ф-12 на гладких і ребристих трубах, при різних температурах насичення, наведені в табл.21.1. У цій таблиці труба 1 має профіль (рис.21.6,а); профіль труби 2 (рис.21.6,б), а труба 3 має прямі круглі ребра, висота яких 3,46 мм, товщина 0,85 мм, крок 1,41 мм.

Таблиця 21.1.

Як видно з табл.21.1 відношення коефіцієнтів тепловіддачі на ребристих трубах до коефіцієнту тепловіддачі, отриманому при кипінні на гладких трубах, незначно залежить від величини теплового потоку і тиску. Основними параметрами, які визначають ефективність ребер з точки зору теплообміну при кипінні, є відношення кроку ребер s до середньої величини просвіту між ребрами d (s/d) і відношення висоти ребер h до d (h/d ).

Візуальні спостереження процесу пароутворення на ребристих трубах показали, що основна маса парових бульбашок утворюється на поверхні труби біля основи ребер. Це пов’язано перед усім з тим, що тут температура поверхні вища. Можливо також, що біля основи ребер більша шорсткість.

Труба 1 має дуже малу відстань між ребрами, а труба 3 – суттєво більшу висоту ребра (3,46 мм) у порівнянні з трубами 1 і 2 (див. табл.21.1 і рис.21.6). Мала відстань між ребрами і більша висота ребер погіршують умови відведення пари, тому при температурі 10 і 20°С спостерігається запарювання труби. У названих умовах для цих труб значення a_р/a_гл = 1. Ураховуючи слабку залежність a_р/a_гл від тиску і теплового потоку при розвиненому кипінні фреонів, орієнтовне значення цієї величини можна визначити як функцію геометрії ребер (табл.21.2).

Таблиця 21.2.

При кипінні фреонів 12 і 22 на пучках ребристих труб, геометрія яких близька до наведених на рис.21.6 приведений коефіцієнт тепловіддачі можна розраховувати по формулі:

a_пр = a_етeп,р, (21.3)

для фреона-12 ; (21.4)

для фреона-22 (21.5)

де a_ет середній коефіцієнт тепловіддачі еталонного (шестирядного) пучка, Вт/(м²·К); q_р – густина теплового потоку, віднесена до одиниці всієї поверхні труби з урахуванням ребер, Вт/м²; e_п,р – поправочний співмножник на число рядів труб у пучці п_р.

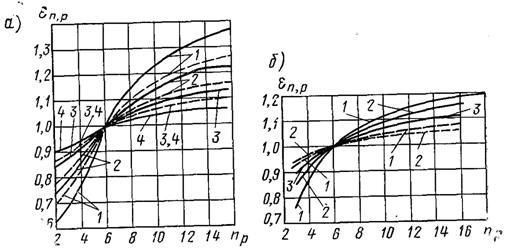
Рис.21.7. Значення коефіцієнта e_р,п при кипінні фреона-12 (а) і фреона-22 (б)на пучці ребристих труб при q_p кВт/м²: 1 – 0,5; 2 – 1,0; 3 – 1,98; 4 – 3,03 ; –––– t₀ = –20; – – – t₀ = –10°C

Значення e_п,р визначається з графіка рис.21.7 в інтервалі зміни теплового потоку від 2 до 7 кВт/м². При кількості рядів у пучці п_р < 10, значення e_п,р » 1.

21.3. Кипіння у тонких плівках рідини

У тонких плівках рідини можливі такі механізми передачі теплоти: випаровування з вільної поверхні плівки; придушене кипіння; розвинене бульбашкове кипіння; плівкове кипіння. У залежності від того чи іншого механізму утворення пари буде по-різному рішатися питання про визначення абсолютних значень тепловіддачі.

Найбільшу зацікавленість представляє режим бульбашкового кипіння у тонкій плівці, як широко розповсюджений в теплообмінних апаратах. Було виявлено, що по мірі зменшення висоти шару рідини над поверхнею теплообміну з певного моменту відбувається зменшення, а далі підвищення коефіцієнту тепловіддачі (рис.21.8).

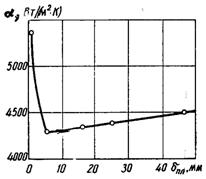
Рис.21.8. Залежність a від dпл за даними Якоба

Подальші дослідження, виконані на дистильованій воді, уточнили характер зміни інтенсивності тепловіддачі зі зміною рівня рідини над горизонтальною поверхнею тепловіддачі. При атмосферному тиску збільшення коефіцієнта тепловіддачі із зменшенням рівня спостерігається при густині теплового потоку до 100 кВт/м². При більших навантаженнях ріст a не спостерігається аж до товщини розриву плівки термокапілярними силами

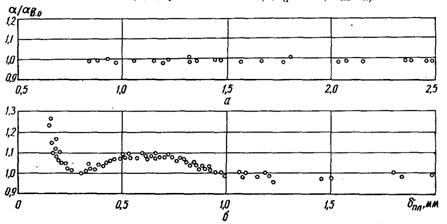
Рис.21.9. Зміна інтенсивності тепловіддачі у випаду потоншення плівки води при q = 610 кВт/м² (а) і q = 26 кВт/м² (б) (р = 0,1 МПа)

(рис.21.9,а). На рис.21.9,б наведено у відносних координатах a/a_в.о найбільш загальний вид залежності a від q, отриманої при густині теплового потоку 26 кВт/м². При більших теплових навантаженнях із-за розриву киплячої плівки при пониженні рівня удається отримати тільки частину такої кривої.

Зараз не існує єдиної думки про причини підвищення коефіцієнта тепловіддачі при потоншенні плівки рідини. Одні автори вважають, що при кипінні у тонкій плівці головним чинником інтенсифікації є турбулізація плівки паровими бульбашками, ефект дії яких у цьому випадку більший, ніж у великому об’ємі. Другі, стосовно криогенних рідин, вважають, що більша інтенсивність тепловіддачі пояснюється меншим термічним опором плівки у порівнянні з термічним опором теплового пограничного шару. Треті, ріст інтенсивності теплообміну пов’язують з підвищеною частотою відриву бульбашок, хоч очевидно, що із зменшенням температури поверхні теплообміну не може відбуватися збільшення частоти.

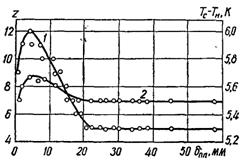
Рис.21.10. Залежність кількості діючих центрів пароутворення (1) і величини перегріву поверхні теплообміну (2) від товщини шару води при q = 28 кВт/м2

Досліди показують, що при зменшенні товщини шару рідини кількість діючих центрів пароутворення у широкому діапазоні зміни товщини залишається постійною і тільки при малих товщина шару (менше 20...30 мм) починає збільшуватися (рис.21.10). Перегрів поверхні також збільшується. Це пояснюється так. При зменшенні висоти шару рідини у певний момент починає зменшуватися частка пари, яка отримується за рахунок випаровування перегрітої рідини у парову бульбашку, і відповідно зменшується коефіцієнт росту парових бульбашок в об’ємі рідини. Внаслідок цього зі зменшенням висоти шару збільшується середня температура рідини і температура поверхні.

При постійному підведенні теплоти до поверхні нагріву, а значить при незмінній кількості утвореної пари, повинен зростати добуток d_в³пf. Спостереження показують, що відривний діаметр d_в зі зменшенням товщини шару залишається практично сталим. Виходить, що повинні зростати кількість діючих центрів пароутворення п і частота відриву парових бульбашок f.

При невеликій кількості на поверхні нагріву діючих центрів переважає їх збільшення, яке може відбуватися тільки внаслідок збільшення температури гріючої поверхні до значення, яке відповідає активації нових центрів. Це видно з рис.21.10, що при зменшенні рівня рідини збільшення кількості діючих центрів відбувається при збільшенні температури поверхні теплообміну.

На поверхні, штучно насиченій великою кількістю діючих центрів, значна частина з них буде працювати зі зменшеною продуктивністю і відповідно з меншою частотою. За цих умов зменшення рівня приводить в основному до збільшення частоти відриву бульбашок на раніше працюючих “в’ялих центрах”.

На рис.21.11 наведена залежність кількості діючих центрів пароутворення від висоти шару рідини для трьох поверхонь, які по різному оброблені. Отримані дані якісно погоджуються з приведеними вище міркуваннями.

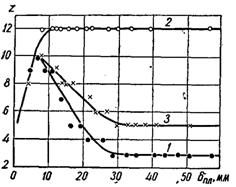
Рис.21.11. Залежність кількості діючих центрів пароутворення від товщини шару води при q = 10 кВт/м2: 1 – збіднена центрами поверхня (полірована); 2 – насичена центрами поверхня; 3 – технічно шорстка поверхня (4...5 клас чистоти по ГОСТ 2789 – 73)

При висоті шару до 1...2 мм починає зменшуватися температура поверхні тепловіддачі, що пов’язано із збільшенням тої частки теплоти, яка передається теплопровідністю і конвекцією у проміжках між центрами пароутворення. Це підтверджується тим, що нахил кривої залежності a = f(d_пл) при d_пл = 0,6...1 мм практично співпадає з нахилом кривої l/d_пл = f(d_пл). Таким чином, збільшення інтенсивності тепловіддачі при зменшенні висоти шару рідини над поверхнею теплообміну пов’язане із збільшенням частки теплоти, яка передається теплопровідністю і конвекцією у проміжках між центрами пароутворення. Отже падіння температури веде до зменшення кількості діючих центрів пароутворення. При цьому випаровування з вільної поверхні плівки компенсує сумарне зменшення паропродуктивності центрів. При товщина плівки води 0,1...0,2 мм кипіння в ній повністю подавлене.

21.4. Кипіння у різних гравітаційних полях

Інтенсивність поля сил тяжіння прийнято характеризувати відносною величиною прискоренням вільного падіння g/g_n = h, яке називають перевантаженням, де g_n = 9,81 м/с² – прискорення сили тяжіння на поверхні Землі (стосовно ослаблених полів, тобто h < 1, термін “перевантаження” є умовним; крім того, силу тяжіння тут слід розуміти як масову силу, обумовлену не тільки тяжінням, а і прискоренням системи).

Діапазон перевантажень, які представляють певний інтерес, дуже широкий. Область значень h < 1 відповідає потребам космічної техніки, але і тут можливі випадки h >1, наприклад, при розгоні і гальмуванні літальних апаратів. Область h >>1 (до значень порядку 1000) зв’язана з перспективами охолодження випаюванням обертальних вузлів різних машин.

Способи реалізації експериментів пов’язаних з відмінністю g від прискорення вільного падіння, різні для різних областей. Умову h >1 можна відносно просто реалізувати в обертальних пристроях типу центрифуги. Для ослабленої сили тяжіння (h < 1) використовуються установки вільного падіння – наземні і в умовах польоту по кеплеровській траєкторії. Тривалість досліду при цьому обмежується секундами. Тривалі періоди невагомості (h » 0) можна отримати на борту штучного супутника Землі під час орбітального польоту. Використовуються також різні способи імітації слабкого поля сили тяжіння, при яких сили тяжіння компенсуються силами інерційної природи (за рахунок магнітних, електродинамічних ефектів, розкладання сили тяжіння при кипінні у плоских нахилених контейнерах).

Можливість впливу прискорення сили тяжіння на кипіння рідин слідує із самої природи цього процесу, де співіснують дві фази з різко відмінними густинами. Можна очікувати, що перевантаження чинить вплив на поведінку, характеристики парових бульбашок і, як наслідок, – на інтенсивність теплообміну.

Ріст парових бульбашок. Відомі співвідношення для росту парових бульбашок (як в об’ємі, так і на твердій поверхні) не включають величину прискорення сили тяжіння, тому що всі вони отримані з нехтуванням її ефектами. Це виправдано, оскільки розглядається та стадія росту, коли рух бульбашки під дією сили тяжіння не є процесом, який визначає інтенсивність підводу тепла до поверхні бульбашки і її зростання.

Вплив прискорення сили тяжіння g на ріст бульбашок може відбуватися двома шляхами. По-перше, внаслідок зміни співвідношення частки теплоти, яка підводиться до бульбашки від основи і сферичної її частини; це співвідношення зв’язане з формою бульбашки, яка за певних умов залежить від g. По-друге, переміщення бульбашки під дією сили тяжіння обумовлює конвективну складову теплового потоку від рідини до поверхні бульбашки; зазвичай нею нехтують, вважаючи, що вона мала у порівнянні з кондуктивною складовою. Роль цих ефектів залежить від розмірів бульбашки. При рості бульбашок на стінці вони проявляються тільки у заключній стадії перед відривом, викликаючи розбіжність дослідних даних з росту бульбашок з розрахунковими співвідношеннями, які не враховують ці ефекти.

Зі сказаного випливає, що помітного впливу прискорення сили тяжіння на ріст бульбашок можна чекати тільки у пізній стадії росту, яка передує відриву бульбашок. Цей висновок підтверджують небагато чисельні дослідні дані, отримані в установці вільного падіння при кипінні води з перевантаженнями h = 0,014...1,0, так і при імітації послабленої гравітації – за допомогою магнітного поля при кипінні кисню (h = 0,02...1,0) чи за допомогою нахилених плоских контейнерів при барботажі азоту в воду (h = 0,017...1,0), при цьому в двох останніх випадках вплив g практично відсутній. Відсутність впливу g на ранніх стадіях росту бульбашок показано також в дослідах при 1< h < 100 (у полі відцентрових сил).

Відривний діаметр бульбашок. Суттєва різниці густини рідини і її пари приводить до того, що у полі сили тяжіння на бульбашку діє результуюча сила гідростатичного тиску. При кипінні на плоскій горизонтальній поверненій вгору (проти прискорення сили тяжіння) поверхні, сила тиску є відривною і її значення пропорційне величині гравітаційного прискорення. Таким чином, прискорення сили тяжіння безпосередньо визначає умови відриву парових бульбашок, при цьому його збільшення повинно вести до зменшення часу контакту бульбашки з поверхнею нагріву і до його відривного розміру. Вплив прискорення сили тяжіння на відривний діаметр бульбашок характеризується залежністю d_в/d_в.п = f(h), де d_в.п – відривний діаметр за умови нормальної сили тяжіння (h = 1). Конкретний вид цієї залежності визначається умовами росту бульбашок. При квазістаціонарному рості на гладкій поверхні згідно (19.2)

d_в/d_в.п = h ^–1/2. (21.6)

При квазістатичному рості на кромці впадини згідно (19.17) чи при швидкому рості (динамічний режим) згідно (19.7) і (19.14)

d_в/d_в.п = h ^–1/3. (21.7)

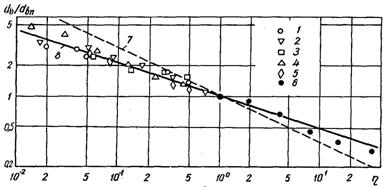
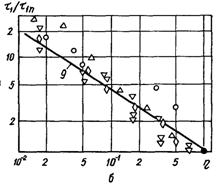
Рис.21.12. Залежність відривного діаметра бульбашок (а) і часу контакту бульбашок з поверхнею нагріву (б) від перевантаження: 1 – кисень у магнітному полі; 2 – ефір у нахиленій щілині; 3, 4 – вода в установці вільного падіння; 5 – барботаж азоту у воду в нахиленій щілині; 6 – вода у центрифузі; 7 – розрахунок за (21.6); 8 – за (21.7); за (21.8)

Дослідна перевірка d_в(h) (в умовах h < 1 – на установці вільного падіння і при імітації послаблення гравітації, h = 1...30 – у центрифузі) показала, що співвідношення (21.7) ближче до дійсності (рис.21.12,а). При порівнянні використовувалися дані, які стосуються динамічного і статичного режимів росту бульбашок. Відмічається також, що при кипінні високов’язких рідин (60%-ний цукровий розчин) вплив h на d_в практично відсутній.

При значних перевантаженнях у рідині виникають помітні градієнти гідростатичного тиску вздовж вектора прискорення і, як наслідок, градієнт локальної температури насичення Т_н(р). При практично однорідному температурному полі об’єму рідини (з температурою Т_р), характерному для розвиненого бульбашкового кипіння, що приводить до наявної зміни різниці Т_р–Т_н за висотою об’єму. При віддалені від вільної поверхні розділу (вздовж вектора, що імітує прискорення сили тяжіння) ця різниця зменшується, і якщо біля вільної поверхні рідини близька до стану насичення, то біля поверхні нагріву за межами тонкого пристінного шару вона буде не догрітою. При великих значеннях h відстані, на яких проявляються ефекти неоднорідності поля гідростатичного тиску і локальної температури насичення, повністю співрозмірні з розмірами бульбашок. Цим створюються специфічні умови росту бульбашок, що, безумовно, впливає на відривні розміри.

Названі особливості не враховуються співвідношеннями, з яких виходять (21.6) і (21.7), тому при h >> 1 не слід чекати збереження залежності d_в(h), характерної для області h < 1. Крім цього, із-за описаних особливостей кипіння при h >> 1 у випадку співставлення даних різних авторів необхідно враховувати різницю у дослідних установках і методик опрацювання дослідного матеріалу. Вимагає також обережності екстраполяції співвідношення (21.7) в області h » 0; з такої екстраполяції слідує висновок про неможливість відриву парових бульбашок в умовах, близьких до повної невагомості.

Характер зміни розміру бульбашки у часі впливає не тільки на значення, але і на знак інерційної реакції рідини. За певних умов вона із сили, яка притискує бульбашку до поверхні нагріву, перетворюється у відривну. Важливу роль при цьому виконує наявність градієнту температури об’єму рідини біля поверхні нагріву. Сповільнення росту бульбашки за межами пристінного шару, пов’язане з виходом її до більш холодних шарів рідини, що приводить до виникнення сили відриву навіть при відсутності поля сил тяжіння.

Частота утворення бульбашок. Збільшення відривних розмірів парових бульбашок зі зменшенням навантаження при збереженні залежності R(t) означає одночасне збільшення часу контакту бульбашки з поверхнею нагріву t₁. При законі росту бульбашки R ~ t^0,5 із співвідношення (21.7) слідує

t₁/t_1п = h ^–2/3. (21.8)

Цей вираз не входить у протиріччя з дослідними даними, хоч їх розкид дуже великий (див. рис.21.12,б). Можливість прямого впливу навантаження на другу складову періоду утворення бульбашок – час очікування t₂ – не повністю очевидна. Мабуть цей вплив здійснюється через масштаби теплового подразнення зростаючими бульбашками пристінного шару рідини і поверхні нагріву в околиці центру пароутворення. Оскільки подразнення збільшуються зі збільшенням відривного розміру бульбашки і часу його перебування на поверхні нагріву, тобто із зменшенням h, відповідно повинен зростати час t₂.

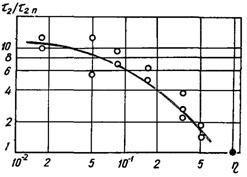
Рис.21.13. Залежність часу очікування від перенавантаження при кипінні ефіру в нахиленій щілині

Дослідні дані при кипінні ефіру з імітацією перенавантажень за допомогою плоских похилих контейнерів підтверджує ці міркування (рис.21.13). У той же час при кипінні кисню у такому ж діапазоні перенавантажень, які імітуються магнітним полем, період очікування не залежно від значення h залишався рівним нулю. В інтервалі h = 1...100 відмічається зменшення t₂ (а також t₁) із збільшенням h пропорційно h ^–1/2.

На підставі небагато чисельних дослідних даних можна зробити висновок про підвищення частоти утворення бульбашок при посиленій гравітації головним чином із-за зменшення їх відривних розмірів. Залежність частоти відриву від перенавантаження має вид

f/f_n = h ^k, (21.9)

де k близьке до 2/3. Мабуть отримані дані не можна вважати повними із-за обмеженості об’єму дослідних даних, на яких вони ґрунтуються.

Інтенсивність теплообміну при бульбашковому кипінні. Перші дослідження тепловіддачі у відмінних від нормальних умовах тяжіння показали практичну відсутність впливу h на інтенсивність тепловіддачі при розвиненому бульбашковому кипінні. Зменшення h від 1 до 0,01 викликають тільки незначні зміни перегріву поверхні (зменшення при горизонтальному положенні нагрівача і збільшенні при вертикальному) в межах природного розкидання дослідних даних. Ці результати отримані при різних способах імітації ослаблення гравітаційних полів для різних рідин (вода, етанол, водень, кисень, азот, вуглеводні).

Дослідження кипіння при імітації послаблення поля за допомогою магнітного поля (кисень) і нахилених контейнерів (ефір, етанол, вода) підтвердили висновок про слабку чутливість інтенсивності теплообміну до дії гравітації. До такого ж висновку приводять результати дослідження кипіння води і фреону у полі відцентрових сил (h = 1...5000). Але у цих же дослідженнях зі збільшенням h виявлено збільшення інтенсивності тепловіддачі у режимі нерозвиненого бульбашкового кипіння і зв’язаного з цим затягуванням переходу до розвиненого кипіння в області більш високих густин теплового потоку. Це відбувається із-за підсилення вільного руху рідини зі збільшенням h.

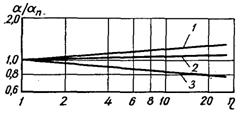
Рис.21.14. Вплив перенавантаження на відносний коефіцієнт тепловіддачі при кипінні насиченої води при q, кВт/м²: 1 – 60; 2 – 250; 3 – 450

При збільшенні густини теплового потоку, коли основним процесом, який визначає інтенсивність тепловіддачі, стає пароутворення (тобто режим розвиненого бульбашкового кипіння), ефект h практично зникає, чи навіть, за деякими даними, стає зворотним (рис.21.14). Мабуть, впливом перенавантаження на інтервал теплових навантажень, при якому відбувається перехід до розвиненого бульбашкового кипіння, і на інтенсивність тепловіддачі у режимі нерозвиненого бульбашкового кипіння можна пояснити певне протиріччя даних залежності a(h ) в області h > 1.

Отже, не дивлячись на помітний вплив прискорення сили тяжіння на зовнішню картину процесу, яка проявляється в одночасній зміні відривного розміру і частоти утворення бульбашок, будь-яких суттєвих змін механізму тепловіддачі при розвиненому бульбашковому кипінні не відбувається. У цьому ще раз проявляється притаманна бульбашковому кипінню консервативність основних процесів, які визначають інтенсивність тепловіддачі, – практична незалежність їх від зовнішньої дії.