24.4. Теплообмін при кипінні в трубах і каналах

В оптимальних умовах коефіцієнт тепловіддачі a при кипінні в трубах практично залишається постійним по висоті труби і дорівнює a при кипінні у великому об’ємі. Середнє значення a для всієї труби у цьому разі досягає максимуму. Відповідний максимуму a оптимальний гідродинамічний режим (швидкість циркуляції і висоту п’єзометричного рівня) можна визначити за методикою викладеною у попередньому параграфі, а коефіцієнт тепловіддачі за рівнянням для a при кипінні в умовах вільного руху.

Зроблений ще у 40-х роках минулого століття висновок про можливість розрахунку теплообміну при кипінні в трубах за формулами для інтенсивності теплообміну при кипінні у великому об’ємі пізніше отримав підтвердження дослідженнями багатьох авторів як при кипінні в трубах і каналах насичених рідин, так і при кипінні з недогрівом. Це пояснюється існуванням широкої області режимних параметрів, у якій визначальною величиною для інтенсивності теплообміну є тільки теплове навантаження поверхні нагріву.

Забезпечення оптимального режиму важливе для випарників з паровим обігрівом, особливо у тих випадках, коли значення a при кипінні малі (наприклад, при кипінні в’язких рідин і розчинів). Можливість реалізації такого режиму (з постійним a по висоті труби) залежить від багатьох факторів. У багатоступінчатих установках така можливість полегшується завдяки надходженню перегрітої рідини з попередньої ступені, при цьому скорчується довжина економайзерної ділянки. В одноступінчатих установках помітну роль відіграє сполучення ряду факторів, таких як тиску, теплового навантаження, геометричних розмірів труб та ін. Чим менший тиск і теплове навантаження, тим меншим повинно бути відношення висоти труби до її діаметра. Для одноступінчатих промислових випарників (при біля атмосферному тиску і помірних теплових навантаженнях) відношення Н/D відповідає оптимуму, який знаходиться в межах 50...150.

Довжина економайзерної ділянки, при інших рівних умовах, залежить від тиску в циркуляційному контурі. Це пояснюється різними значеннями ді/др при низьких і високих тисках. Так, наприклад, для води при р = 50 кПа ді/др = 2 Дж/(кг·Па), а при р = 5 МПа ді/др = 0,06 Дж/(кг·Па). В одноступінчатих випарниках низького тиску із-за підвищеного недогріву довжина економайзерної ділянки може бути значною. Для її зменшення необхідно працювати при малих швидкостях циркуляції.

Під час аналізу і розв’язку задачі про інтенсивність теплообміну в умовах вимушеного руху киплячої рідини виникають додаткові (у порівнянні з кипінням у великому об’ємі) труднощі. Вони викликані розмаїттям форм течії парорідинної суміші, необхідністю враховувати гідродинамічну дію потоку на процес пароутворення, а також процеси термічної і механічної взаємодії між фазами на границі розділу. З метою наочності і спрощення рішення зі всього розмаїття умов, в яких може відбуватися процес теплообміну при кипінні в трубах і кільцевих каналах, допустимо виділити п’ять основних режимів. У межах кожного з виділених режимів відбуваються характерні для нього співвідношення між параметрами (q, w₀, b і р), які визначають притаманний вплив того чи іншого механізму переносу тепла (чи одночасний їх вплив) на інтенсивність теплообміну.

1. Одним з таких режимів можна виділити область параметрів, у яких інтенсивність теплообміну повністю визначається механізмом переносу, обумовленого процесом пароутворення (розвинене бульбашкове кипіння). У цій області коефіцієнт тепловіддачі не залежить від швидкості парорідинної суміші і значить від паровмісту потоку (безумовно у характерному для цього режиму інтервалу зміни b). На рис.24.5 цьому випадку відповідають горизонтальні ділянки кривих a = a (b) при q = const і w = const.

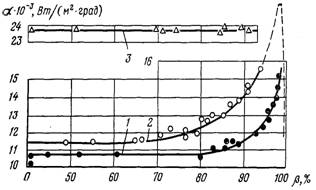
Рис.24.5. Залежність коефіцієнта тепловіддачі a від об’ємного витратного паровмісту b : 1 – w₀ = 0,5 м/с, q =232 кВт/м²; 2 – w₀ = 1,0 м/с, q =232 кВт/м²; 3 – w₀ = 0,5 м/с, q =815 кВт/м²

2. Друга область режимних параметрів характеризується високими значеннями не тільки густини теплового потоку, а і паровмістом. У цій області паровміст, а значить і дійсна швидкість рідкої фази на стільки велика, що на механізм переносу, обумовлений процесом пароутворення, накладається вплив механізму турбулентного обміну в однофазному середовищі [висхідні ділянки кривої a = a (b)].

3. При низьких значеннях q і b (b ® 0) процес пароутворення і паровмісту потоку не впливає на коефіцієнт тепловіддачі при кипінні. У цій області режимних параметрів тепло переноситься в потоці рідини за допомогою звичайного турбулентного обміну, який діє в однофазних середовищах.

4. Область режимних параметрів, де процес пароутворення не впливає на інтенсивність теплообміну, але паровміст змінюється у широких межах. У цій області при заданому значенні теплового потоку і незмінних масових витратах парорідинної суміші коефіцієнт тепловіддачі суттєво залежить від паровмісту і збільшується з його ростом.

5. Необхідно виділити область режимних параметрів, яка характеризується висиханням плівки рідини, яка рухається стінкою труби (низхідна гілка кривої 2 на рис.24.5). Тет при висиханні плівки коефіцієнт тепловіддачі зменшується від деякого максимального значення до мінімального, який відповідає коефіцієнту тепловіддачі до перегрітої пари, масові витрати якої дорівнюють масовим витратам парорідинної суміші. Цю область називають областю погіршених режимів тепловіддачі.

Режими погіршеного теплообміну, якщо вони установлюються навіть на частині поверхні теплообміну апарата, зменшують значення коефіцієнта тепловіддачі для всієї поверхні в цілому. Але такі режими у багатьох випадках повністю виключити неможливо. У прямоточних парогенераторах, у деяких типах випарників холодильних машин вони завжди мають місце.

Інтенсивність теплообміну при кипінні в умовах вимушеного руху рідини при малих паровмістах можна розрахувати по формулі:

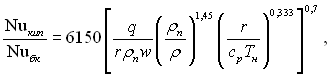(24.27)

де Nu_кип – число Нуссельта в процесі тепловіддачі при кипінні; Nu_бк – число Нуссельта для умов теплообміну при відсутності кипіння, яке можна розраховувати за (6.465)...(6.467) чи по іншим рівнянням конвективного теплообміну.

Область режимних параметрів, у якій механізм процесу обумовлений процесом пароутворення, не впливає на інтенсивність теплообміну при кипінні визначається умовою:

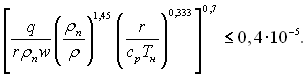(24.28)

При дотриманні умови (24.28) Nu_кип = Nu_бк коефіцієнт тепловіддачі теж розраховується за (6.465)...(6.467) чи по іншим рівнянням конвективного теплообміну при турбулентному русі.

При зворотному знаку нерівності (24.28) інтенсивність теплообміну практично повністю визначається процесом пароутворення. У цьому випадку коефіцієнт тепловіддачі розраховується по формулі (24.27). В області режимних параметрів, де коефіцієнт тепловіддачі залежить від паровмісту [горизонтальні ділянки кривих a = a (b) на рис.24.5], при розрахунку a у формули (24.27) і (6.465)...(6.467) можна підставляти швидкість рідини на вході в трубу, тобто швидкість циркуляції w₀.

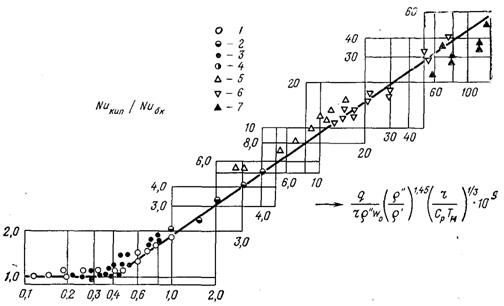
Рис.24.6. Співставлення дослідних значень коефіцієнтів тепловіддачі при кипінні в умовах вимушеного руху з узагальнюючою залежністю (24.27) при тиску р, МПа: вода 1 – 0,196; 2 – 0,686; 3 – 0,392; 4 – 16,65; етанол 5 – 1,12; 6 – 3,06; 7 – 5,1

Дослідні дані, які відносяться до цієї області режимних параметрів, наведені на рис.24.6 і співставленні з розрахунковою залежністю (24.27). Значення Nu_бк і К_w (перший співмножник абсциси) розраховувалися за швидкістю циркуляції. З рисунка видно, що погодження розрахункових і дослідних даних a задовільне. Формула (24.27) задовільно узагальнює дослідні дані і для інших рідин, таких як п-бутана, п-пропана, кисню, бензолу і дифенілу.

Слід відмітити, що граничне значення паровмісту b_гр, до якого можна вести розрахунок коефіцієнта тепловіддачі за швидкістю циркуляції, залежить від фізичних властивостей рідини, тиску, густини теплового потоку і швидкості. Для води при тисках до 1,0...1,5 МПа воно знаходиться у межах 0,6...0,9. При високих тисках значення b_гр менше. Формул для визначення b_гр на сьогоднішній день не існує, але при b > 0 розрахунок a по формулі (24.27) можна виконувати за середньою дійсною швидкістю рідкої фази w = w₀/(1 – j). В умовах бульбашкової, снарядної і плівкової (кільцевої) структур потоку при достатньо великих витратах рідкої фази (орієнтовно при Re₀ = w₀d/n > 30000 і при Fr_см> 6) підстановка у формулу (24.27) швидкості w дає задовільне погодження розрахункових значень a з дослідними.

На рис.24.7 у координатах, які відповідають формулі (24.27), наведені дослідні дані отримані при кипінні води, етанолу і п-бутану в умовах, коли впливом паровмісту не можна нехтувати. Ці дані стосуються до перерахованих вище структур течії парорідинної суміші, тому в розрахунок вводиться середня швидкість рідини w. При її визначенні дійсний об’ємний паровміст j розраховувався по формулі:

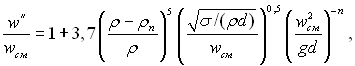(24.29)

де d – діаметр труби, м.

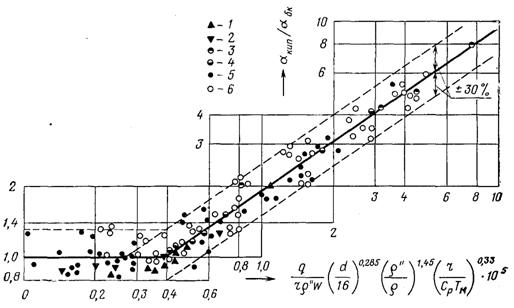
Рис.24.7. Співставлення дослідних значень a з формулою (24.27) при b > 0: вода: 1 – р = 0,196 МПа; 2 – р = 0,686 МПа (0,2 < b < 0,98); 3 – р = 16,65 МПа (0,26 < х < 0,33); етанол: 4 – р = 0,196 МПа (0,2 < b < 0,77); п-бутан:5 – р = 0,145 МПа; 6 – р = 0,33 МПа (0,1 < b < 0,85)

Коефіцієнт пропорційності у формулі (24.27) відповідає отриманим дослідним даним, отриманих на трубі діаметром d = 16 мм. Але при розвиненому бульбашковому кипінні інтенсивність теплообміну не залежить від діаметра труби. Тому, щоб виключити вплив діаметра в умовах розвиненого кипіння, у комплекс, відкладений по осі абсцис на рис.24.7, введений поправочний множник (d/16)^0,285. Показник степеня 0,285 обумовлений тим, що при турбулентній течії однофазної рідини коефіцієнт тепловіддачі обернено пропорційний діаметру в степені 0,2. Поправка на діаметр вводиться і при малих паровмістах, коли розрахунок виконується за швидкістю циркуляції w₀. Отже для труб, діаметр яких суттєво більший чи менший 16 мм отримане по формулі (24.27) відношення a_кип/a_бк необхідно помножати на величину (d/16)^0,2. Це стосується тільки області розвиненого кипіння.

За умови кільцевої (плівкової) структури течії суміші основна маса рідини знаходиться у плівці, а невелика її частина рухається у вигляді крапель у паровій фазі. На поверхні плівки виникають дрібні і крупні хвилі, з гребенів яких краплі зриваються до ядра потоку. Дослідні дані, отримані при вивченні руху рідких плівок, показали, що при постійних витратах рідкої фази з підвищенням швидкості пари висота гребенів хвиль спочатку збільшується, а далі починає зменшуватися. При певних значеннях паровмісту плівкова структура суміші переходить у дисперсно-кільцеву, за якої біля стінки труби залишається тонка плівка рідини, яка рухається з середньою швидкістю w_пл. Більша частина рідкої фази при цьому тече у вигляді дрібних крапель у паровому ядрі потоку з середньою швидкістю w_я. Величина цієї швидкості залежить від ступеня дисперсності і фізичних властивостей рідкої фази, від середньої дійсної швидкості пари w_п і від ряду інших факторів. Зазвичай w_я<w_n.

Коли рідка фаза майже повністю знаходиться в плівці, то можна вважати, що середня швидкість плівки w_пл практично дорівнює середній швидкості рідини w. Відповідно площа поперечного перерізу труби, яка зайнята рідкою фазою f дорівнює площі поперечного перерізу плівки f_пл.

Краплі рідини у ядрі потоку рухаються в області підвищеної швидкості, тому їх середня швидкість перевищує середню швидкість рідини у плівці (w_я > w_пл). Звідси виходить, що середня швидкість рідини у плівці менша швидкості рідини осередненої за всім перерізом труби (w_пл < w). Очевидно, що чим більше крапель рідини рухається в ядрі потоку, тим менша відносна величина швидкості рідини у плівці w_пл/w. Але накопичення крапель рідини не відразу приводить до зменшення величини w_пл/w. Це пояснюється дуже складними процесами взаємодії плівки з ядром і характером утворення хвиль на її поверхні.

Співвідношення між швидкостями w, w_пл і w_я можна отримати з рівняння матеріального балансу, написаного для рідкої фази, тобто із залежності:

wf = w_плf_пл + w_яf_я, (24.30)

де f_я – осереднена площа поперечного перерізу труби, яка зайнята краплями рідини у ядрі.

Ураховуючи, що f = f_пл + f_я, із залежності (24.30) отримаємо

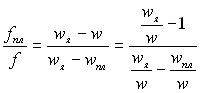. (24.31)

В умовах дисперсно-кільцевої структури парорідинної суміші інтенсивність теплообміну визначається дійсною швидкістю рідини у плівці, яка може бути суттєво меншою величини w. Із-за недостатньої об’єму інформації не можна зараз з необхідною точністю розрахувати параметри, які характеризують рух плівки (витрати рідини у плівці, її товщину і розподіл швидкості за її перерізом). У зв'язку з цим запропонований метод, який дає можливість, минаючи безпосередні виміри, знайти ефективне значення швидкості рідини у плівці w_еф за якою визначаються інтенсивність теплообміну і гідродинамічний опір при дисперсно-плівковій структурі. Метод ґрунтується на уяві, що у двофазному потоці при певному сполученні режимних параметрів (так само як і в однофазному) установлюються співвідношення між інтенсивністю теплообміну і гідродинамічним опором.

Коли витрати рідкої фази достатньо великі (Re₀ > 30000, а Fr_см > 6), то при усіх структурах потоку, які передують дисперсно-плівковій, величиною w визначається не тільки інтенсивність теплообміну, але і втрати тиску, обумовлені опором тертя Dр_тр. За цих умов при адіабатній течії двофазного потоку перепад тиску Dр_тр можна розраховувати так само, як і однофазному потоці, за формулою:

(24.32)

де w – дійсна середня швидкість рідкої фази.

Коефіцієнт гідродинамічного опору z при цьому розраховується по відповідним формулам однофазного потоку у залежності від числа Рейнольдса рідини.

За дисперсно-плівкової структури потоку, коли внесення крапельної вологи з поверхні плівки досягає значної величини опір тертя можна розраховувати за формулою (24.32), якщо до неї підставити певну ефективну швидкість рідини у плівці w_еф. Ефективна швидкість – це умовна швидкість рідини у плівці, при підстановці якої у формулу (24.32) розрахункове значення опору тертя при адіабатній течії двофазного потоку співпадає з дослідним. Величину w_еф можна визначити за даними рис.24.8. Графік, наведений на цьому рисунку побудований на основі дослідних даних, отриманих при дослідженні опору тертя в адіабатному пароводяному потоці. У розглядуваних умовах значенням w_еф визначається інтенсивність теплообміну.

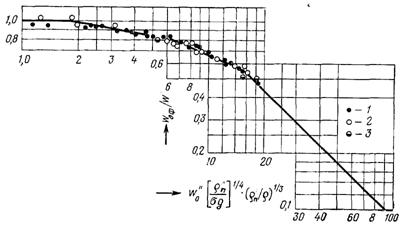
Рис.24.8. Залежність w_еф/w від безрозмірної швидкості пари для пароводяного потоку при р, МПа: 1– 4,9; 2 – 9,8; 3 – 14,7

З рис.24.8 видно, що за умови

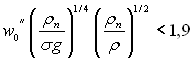
відношення w_еф/w = 1. Якщо значення комплексу, який відкладений по осі абсцис, перевищує 1,9, то до розрахункових формул для визначення опору тертя і інтенсивності теплообміну необхідно вводити w_еф.

На рис.24.9 дослідні значення a, отримані в дослідах при кипінні води в трубах діаметрів 8, 12 і 18 мм при тисках від 1,1 до 3,1 МПа, узагальнені в координатах, які відповідають формулі (24.27). При цьому значення коефіцієнтів тепловіддачі без кипіння a_бк і число подібності К_w визначалися за ефективною швидкістю рідини у плівці (рис.24.8).

З рис.24.9 видно, що при дисперсно-плівковому режиму течії тангенс кута нахилу прямої, який характеризує область розвиненого кипіння, становить 0,55, а не 0,7, як це було при структурах суміші, які передують дисперсно-плівковій. Це пояснюється тим, що у розглядуваних умовах навіть при дуже великих густинах теплового потоку проявляється вплив швидкості суміші. У відповідності з рис.24.9 для дисперсно-плівкового режиму течії суміші формула (24.27) набуває наступного вигляду:

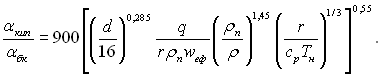(24.33)

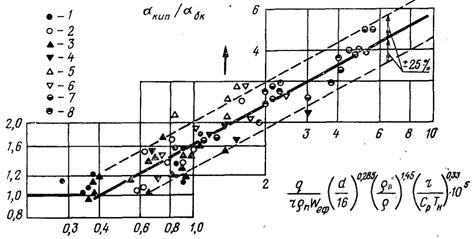
Рис.24.9. Узагальнення дослідних даних в координатах, які відповідають формулі (24.27) (розрахунок за w_еф для води): 1…3 – d = 8, 12,18 мм, р = 1,08 МПа; 4 – d = 12 мм, р = 1,86 МПа; 5…6 – d = 8, 12 мм, р = 2,55 МПа; 7…8 – d = 12,18 мм, р = 3,04 МПа

Коли значення комплексу, який знаходиться у квадратних дужках частини формули (24.33), менше 0,4·10^–5, то a_кип = a_бк. При цьому a_бк розраховується за ефективною швидкістю w_еф.

Таким чином формули (24.27) і (24.33) охоплюють чотири з п’яти виділених областей режимних параметрів, розрізняються між собою по механізму переносу тепла і відповідно по інтенсивності теплообміну. Однак для визначення коефіцієнта тепловіддачі при великих паровмістах необхідно попередньо розрахувати величину j, а при дисперсно-плівковому режимі, крім цього і значення ефективної швидкості w_еф. Але необхідно пам’ятати, що розрахунок коефіцієнта тепловіддачі по величині w можна виконувати тільки при достатньо великих витратах рідкої і парової фаз.

Коефіцієнт тепловіддачі до двофазного потоку можна розраховувати по формулі, в якій аргументами є величини, що безпосередньо задаються умовами. Коли інтенсивність теплообміну не залежить від швидкості середовища і визначається тільки процесом пароутворення, така формула має вид:

(24.34)

У цьому рівнянні число Стантона –

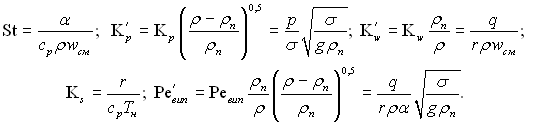
У цій залежності число Стантона St і число К_wў розраховуються по швидкості суміші рідини і пари w_см = w_0ў + w_0І. У К_wў і Реў_вип входить швидкість пароутворення, яка визначається густиною рідкої фази q/(rr). Ця швидкість представляє собою об’ємну кількість рідини, яка перейшла до парової фази з одиниці поверхні тепловіддачі в одиницю часу.

Формула (24.34) справедлива за умови, якщо комплекс

(24.35)

Область режимних параметрів, де проявляється сумісна дія швидкості середовища і процесу пароутворення при великих паровмістах потоку, в узагальненій формі визначається умовою:

0,01·10^–5 < М < 0,3·10^–5. (24.36)

У цій області коефіцієнт тепловіддачі визначається з формули:

(24.37)

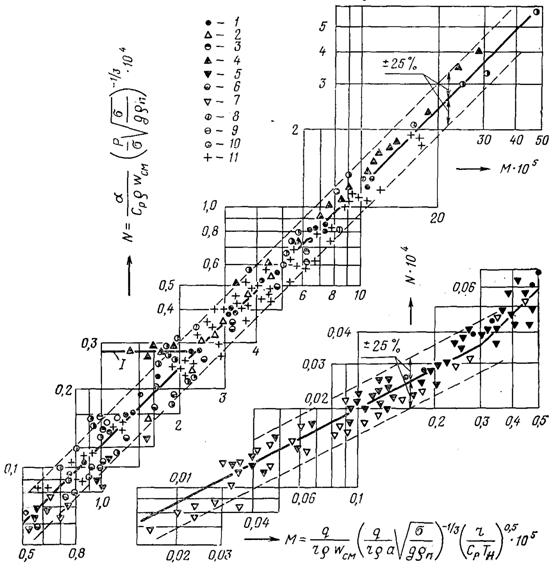
Рис.24.10. Співставлення формул (24.34) і (24.37) дослідними даними: 1...5 – вода, р = 0,1...19,6 МПа; 6 – етанол, р = 0,196 МПа; 7 – фреон-12, р = 0,392 МПа; 8 – фреон-22, t_н = 283 К; 9 – кисень, р = 0,098 МПа; 10 – п-пропан, р = 0,294, 0,647 і 1,175 МПа; 11 – п-бутан, р = 0,14 і 0,3 МПа

Співставлення формул (24.34) і (24.37) з дослідними даними наведено на рис.24.10, з якого видно, що відхилення більшості дослідних значень a від розрахункових не перевищує ±25% навіть при дуже великих паровмістах, які включають дисперсно-плівкову структуру течії парорідинної суміші.

Перехід від плівкової структури потоку до дисперсно-плівкової супроводжується зменшенням гідродинамічного опору і інтенсивності теплообміну. Але, доки на стінці зберігається суцільна рідка плівка, значного зменшення інтенсивності теплообміну не відбувається. Тому у цій перехідній області коефіцієнт тепловіддачі можна розраховувати по формулі (24.37), але точність розрахунку буде трохи меншою. Різке падіння коефіцієнта тепловіддачі спостерігається тільки після початку процесу висихання рідкої плівки (режим погіршеної тепловіддачі). Цей режим формулою (24.37) не охоплюється.

Необхідно мати на увазі, що навіть при дотриманні умови (24.35) процес пароутворення може не здійснювати вплив на інтенсивність теплообміну (область режимних параметрів, яка характеризується відносно низькими значеннями густини теплового потоку). У цій області при незмінних масових витратах парорідинної суміші коефіцієнт тепловіддачі практично не залежить від величини питомого теплового потоку. Тому дослідні значення a, які відносяться до цієї області, отримані при постійних масових витратах суміші і паровмісту b, на рис.24.10 групуються біля горизонтальних прямих, які відповідають різним значенням швидкості циркуляції w₀. На рис.24.10 нанесена одна з горизонтальних прямих (пряма І), яка узагальнює дослідні дані для води при р = 0,098 МПа, w₀ = 5,5 м/с і b = 0. Точки перетину таких горизонтальних прямих з похилою лінією, яка характеризує тепловіддачу в умовах розвиненого кипіння, визначають граничне мінімальне значення густини теплового потоку q_гр,мін (при р, w₀ і b = 0), нижче якого процес пароутворення не впливає на інтенсивність теплообміну. При b > 0 і тих же масових витратах парорідинної суміші дійсна швидкість рідкої фази буде більшою. У цьому випадку граничне значення теплового потоку q_гр більше його мінімального значення, установленого для b = 0.

При густині теплового потоку меншому за граничний, коефіцієнт тепловіддачі за умови турбулентного режиму руху можна розраховувати за любою з формул, які задовольняють дослідні дані, наприклад за формулою М.А.Міхеєва:

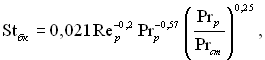(24.38)

де St_бк, Re_р і Pr_р – відповідно число Стантона, Рейнольдса і Прандтля, в яких фізичні властивості рідини визначаються при температурі насичення; Pr_ст. –число Прандтля рідини, значення якого визначається при температурі стінки.

Таким чином при розрахунку коефіцієнта тепловіддачі по формулах (24.34) і (24.37) перед усім необхідно виявити, до якої області режимних параметрів відносяться задані для розрахунку a умови. Для цього необхідно співставити значення коефіцієнтів a_кип і a_бк, розрахованих відповідно за формулами (24.34) чи (24.37) і (24.38). Якщо внаслідок розрахунків виходить, що a_кип < a_бк, то це значить, що ми знаходимося в області турбулентного обміну в однофазному середовищі і інтенсивність теплообміну визначається значенням a_бк. Протилежний наслідок розрахунку (a_кип > a_бк) свідчить про те, що ми знаходимося в області розвиненого кипіння, де інтенсивність теплообміну визначається значенням a_кип.

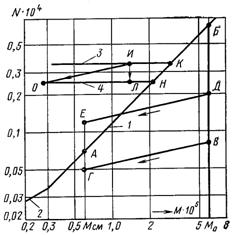
Рис.24.11. До методики розрахунку a за формулою (24.34): 1 – розрахункова крива, яка відповідає формулі (24.34); 2 – те саме, для формули (24.37); 3 і 4 – залежності N_бк = f(M) при b = 0

Розрахункова схема наведена на рис.24.11. На цьому рисунку по осі абсцис відкладений комплекс М, по осі ординат – комплекс NєSt/(Kў_p)^–1/3.

При заданому значенні комплекса М = М_см (b > 0) шукане значення N_кип.см = St_кип.см(Kў_p)^–1/3 визначається точкою А, де St_кип.см = a_кип / (с_рrw_см). Комплекс М, розрахований за швидкістю циркуляції w₀ при тому ж значенні q дорівнює М₀ = М_см(w_см/w₀). Значення N = N_кип,0 = [a_кип / (с_рrw₀)](Kў_p)^–1/3, яке відповідає комплексу М₀, на рис.24.11 відмічено точкою Б. Тому що комплекси М_см і М₀ відрізняються між собою тільки величиною швидкості, яка в області розвиненого кипіння не впливає на інтенсивність теплообміну, то коефіцієнт тепловіддачі у точках А і Б рівні між собою.

Підставляючи значення швидкості циркуляції w₀ у формулу (24.38), визначаємо величини St_бк,0 = a_бк / (с_рrw₀), а далі і комплекс N_бк,0 = St_бк,0 (Kў_p)^–1/3 (точка В на рис.24.11). Тому що точка В лежить нижче точки Б, то це значить, що при заданій густині теплового потоку при w = w₀ коефіцієнт тепловіддачі a_кип > a_бк. Однак при збільшенні швидкості від w₀ до w_см величина a_бк буде збільшуватися, в той час як a_кип залишається без зміни. Для того щоб визначити, чи збережеться при заданому значенні швидкості суміші w_см установлене для w = w₀ співвідношення між a_кип і a_бк, необхідно на рис 24.11 провести лінію, яка визначає залежність St_бк(Kў_p)^–1/3 = f(w) при q = const. Для даної рідини це буде пряма лінія ВГ, тангенс кута нахилу якої дорівнює 0,2. Це слідує з того, що коефіцієнт тепловіддачі a_бк, який входить у число St_бк, при турбулентному режимі течії середовища збільшується зі збільшенням швидкості пропорційно величині w^0,8. Як видно з рис.24.11, у нашому випадку точка Г лежить нижче точки А, отже і при w = w_см інтенсивність теплообміну визначається тільки процесом пароутворення. Коефіцієнт тепловіддачі при цьому визначається з числа St_кип.см = a_кип / (с_рrw_см).

Якщо внаслідок розрахунку вийде, що значення комплексу N_бк,0 на рисунку визначиться, наприклад, точкою Д, то при збільшенні швидкості від w₀ до w_см процес пароутворення перестає впливати на інтенсивність теплообміну (точка Е лежить вище точки А), і значення коефіцієнта тепловіддачі при заданих нами умовах необхідно визначати по формулі (24.38). У цьому випадку у формулу (24.38) необхідно підставити (у залежності від заданих умов) чи дійсну середню швидкість рідкої фази w, чи значення w_еф.

Отже, якщо розрахунок інтенсивності теплообміну при кипінні виконувати за формулами (24.34) і (24.38), то тільки в одному з чотирьох виділених нами режимів необхідне знання дійсної швидкості w чи w_еф, це тільки тоді, коли процес пароутворення не впливає на інтенсивність теплообміну при b > 0.

У формулу (24.34) не входять діаметр труби і в’язкість рідини, але в ній правильно відбивається вплив цих параметрів на процес переходу від конвективного теплообміну в однофазному середовищі до розвиненого кипіння. Дійсно, у турбулентному однофазному потоці рідини із збільшенням діаметра труби від d₁ до d₂ (при w₀ = const) інтенсивність теплообміну зменшується у (d₂ / d₁)^0,2 рази, а при збільшенні швидкості циркуляції від w₀₁ до w₀₂ (при d = const) збільшується в (w₀₂ / w₀₁)^0,8 рази. Якщо d₂ / d₁ при w₀ = const дорівнює w₀₂ / w₀₁ при d = const, то як у першому, так і в другому випадках число St_бк зменшується в одну і ту ж кількість разів, а саме (d₂ / d₁)^0,2 = = (w₀₂ / w₀₁)^0,8.

На рис.24.11 наведені дві горизонтальні прямі 3 і 4, які характеризують тепловіддачу при турбулентній течії однофазної рідини (b = 0) при різних швидкостях циркуляції і діаметрах труби. Вважаючи, що інтенсивність теплообміну в однофазному потоці при заданих значеннях w₀₁, d₁ і q₁ характеризується на рис 24.11 точкою И. При цих значеннях швидкості і діаметра перехід до розвиненого кипіння відбувається у точці К, тобто при густині теплового потоку q_K. Зі збільшенням діаметра труби від d₁ до d₂ при незмінних значеннях w₀ і q точка И зміщується по вертикалі вниз, наприклад у точку Л. У нових умовах (при d = d₂ ) перехід до розвиненого кипіння відбудеться у точці Н, абсциса якої менша абсциси точки К в (d₂ / d₁)^0,2 рази, тому що тангенс кута нахилу розрахункової кривої 1 дорівнює одиниці. Величину М, яку відкладено на рис 24.11 по осі абсцис, можна представити у вигляді добутку С(q^2/3/w), де С – степеневий комплекс, який складається з величин, що характеризують властивості середовища. Отже, абсциси точок Н і К знаходяться між собою у співвідношенні:

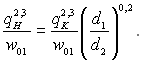
Звідки

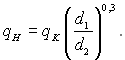(24.39)

Із співвідношення (24.39) виходить, що зменшення інтенсивності теплообміну, обумовлене ростом діаметра труби тягне за собою зменшення значення граничного теплового потоку, при якому припиняється вплив швидкості.

Зі збільшенням швидкості циркуляції при d = const і q = const точка И зміщується вниз по прямій, тангенс кута нахилу якої дорівнює 0,2. Якщо відношення швидкостей дорівнює відношенню діаметрів, як у попередньому випадку, то точка И переміститься у точку О. Таким чином, і у цьому випадку розвинене кипіння настає при тепловому потоці, який відповідає точці Н. Але при більшій швидкості значення q_H буде меншим, але суттєво більшим q_К. У цьому легко переконатися, якщо співставити абсциси точок Н і К:

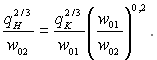
звідки

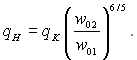
Така різка залежність граничного теплового потоку від швидкості циркуляції пояснюється не тільки різною турбулентністю середовища при різних швидкостях, але і тим, що в міру наближення до розвиненого кипіння в умовах підвищеної швидкості відбувається при меншій температурі стінки і, значить, при меншій кількості активних центрів пароутворення. Для компенсації цього ефекту необхідне додаткове збільшення теплового потоку. При w₀ = const перехід до розвиненого кипіння в трубі великого діаметра відбувається за більш сприятливих для процесу пароутворення умовах.

Аналогічний аналіз можна виконати відносно впливу в’язкості рідини. ЇЇ збільшення від m₁ до m₂ при усіх інших рівних умовах також призводить до зменшення значення граничного теплового потоку. Якщо інтенсивність теплообміну в однофазному середовищі розраховувати за формулою (24.38), то між тепловими потоками q_Н і q_K установлюється наступне співвідношення:

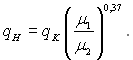
У свій час було запропоновано просту інтерполяційну формулу для розрахунку коефіцієнта тепловіддачі при кипінні в умовах вимушеного руху

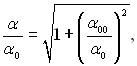(24.40)

де a коефіцієнт тепловіддачі до вимушеного потоку киплячої рідини; a₀ – коефіцієнт тепловіддачі при вимушеному русі однофазного потоку; a₀₀ – коефіцієнт тепловіддачі при розвиненому бульбашковому кипінні, коли вже не проявляється швидкість руху.

Коефіцієнт тепловіддачі a₀₀ визначається по формулі:

a₀₀ = Сq^0,7, (24.41)

де С – коефіцієнт, значення якого визначається з рис.24.12.

В основі формули (24.40) лежить ідея про те, що при кипінні рідини співвідношення між інтенсивністю механізма переносу, обумовленого процесом пароутворення, і інтенсивністю турбулентного обміну в однофазному середовищі можна оцінити співвідношенням між відповідними коефіцієнтами тепловіддачі. На рис.24.13 наведені дослідні дані, які задовільно описуються формулою (24.40).

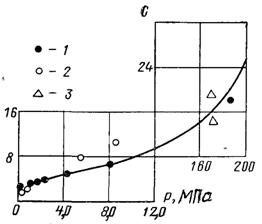
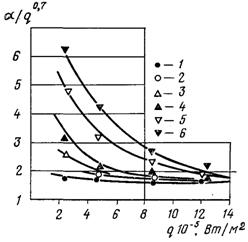
­ Рис.24.12.Залежність коефіцієнта С у формулі (24.41) від тиску за даними різних авторів

Рис.24.13. Залежність a/q^{0, 7} від w₀ і q за дослідами різних авторів (для води, р =0,196 МПа, d = 16 мм) при w₀, м/с: 1 – 0,5; 2 – 1,0; 3 – 2,0; 4 – 3,0; 5 – 5,0; 6 – 6,7 м/с­

Формула (24.40) використана при апроксимації дослідних даних, отриманих при кипінні води в трубах і кільцевих каналах при великому паровмісті, набула наступного виду:

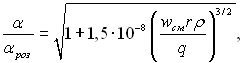(24.42)

де a – коефіцієнт тепловіддачі при кипінні в трубах при великих паровмістах; a_роз – розрахункове значення за формулою (24.40).

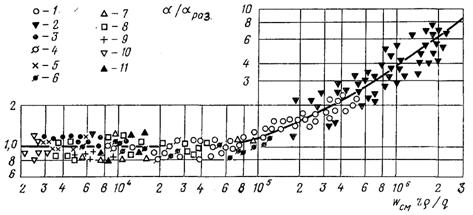
Рис.24.14. Співставлення розрахункової залежності (24.42) з дослідами на воді: труби: 1 – d = 8, 12 і 18 мм, р = 0,489...3,03 МПа; 2– d = 86,95 мм, р = 0,196...0,686 МПа;

3 – d = 8 мм, р = 16,6 МПа; 4 – d = 16 мм, р = 0,686 МПа; 5 – d = 4 мм, р = 0,098...0,88 МПа; 6 – d = 13,75 мм, р = 1,96...7,83 МПа; 7 – d = 10 мм, р = 7,83 і 9,8 МПа;8 – щілина d_ек = 1 і 0,5 мм, р = 4,9 і 14,7 МПа; 9 – труба d = 32 мм, р = 29,3 і 3,91 МПа;10 – пучок d_ек = 19,47 мм, р = 4,9 і 9,8 МПа; 11– щілина d_ек = 6,76 і 3,87 мм, р = 4,9 і 9,8 МПа;

При визначенні величини a_роз рекомендується коефіцієнт тепловіддачі a₀₀ розраховувати за формулою:

(24.43)

де р – тиск, МПа; q – густина теплового потоку, Вт/м².

Формулу (24.42) можна використовувати для розрахунку коефіцієнта тепловіддачі при кипінні води в трубах і в кільцевих каналах при великих паровмістах. В інтервалі тиску від 0,1 до 17,0 МПа вона задовільно погоджується з дослідними даними (рис.24.14).

Усі зазначені вище формули можна використовувати для розрахунку інтенсивності теплообміну при кипінні не тільки у вертикальних, але і в горизонтальних трубах, якщо в останніх не спостерігається розшарування течії парорідинної суміші. Формули придатні також і для розрахунку коефіцієнта тепловіддачі при кипінні в кільцевих каналах. У цьому випадку розрахунок ведеться за еквівалентним діаметром d_ек, а поправка на діаметр у формулі (24.27) вводиться у вигляді (d_ек/16)^0,285.

При кипінні парорідинної суміші в кільцевому каналі інтенсивність теплообміну не залежить від умов обігріву і від ширини щілини. При одній і тій же густині теплового потоку значення коефіцієнта тепловіддачі при кипінні на внутрішній і на зовнішній трубі за умов двостороннього нагріву і при односторонньому обігріві однакове. Вплив ширини кільцевого зазору проявляється тільки тоді, коли діаметр парової бульбашки під час відриву від поверхні теплообміну є спів розмірним з шириною щілини.

Наведені вище формули дають можливість розрахувати інтенсивність теплообміну при кипінні рідин на поверхні чистих труб, тобто не покритих шаром накипу. Оксидна плівка, яка утворюється на поверхні труби, може суттєво впливати на значення коефіцієнта тепловіддачі при кипінні.

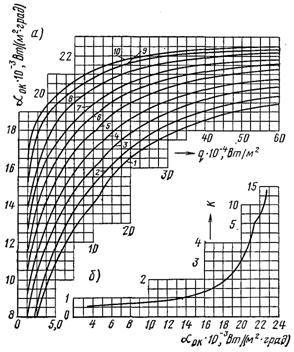
Рис.24.15. Залежність коефіцієнта тепловіддачі a_ок від густини теплового потоку і тиску при кипінні води на поверхні окисленої труби при р, МПа: 1 – 0,98; 2 – 1,96; 3 – 3,32; 4 – 5,88; 5 – 7,84; 6 – 9,8; 7 – 11,76; 8 – 14,65; 9 – 17,6; 10 – 19,6

У трубах парових котлів коефіцієнт тепловіддачі до киплячої води можна визначати за графіками наведеними на рис.24.15. Для окислених труб a_ок вибирається у залежності від тиску і густини теплового потоку по кривій рис.24.15,а. При кипінні води у трубах з нержавіючої сталі (чиста поверхня) коефіцієнт тепловіддачі a визначається із співвідношення a_ч = Кa_ок у якому величина поправочного співмножника для нержавіючих труб К знаходиться по графіку (рис.24.15,б).

З рис.24.15,б видно, що при малих значеннях a_ок, які спостерігаються при низьких теплових потоках, поправочний співмножник менший одиниці. Це можна пояснити, якщо розглянути причини, які обумовлюють вплив накипу на значення a при кипінні. При наявності на поверхні труби шару окислів частина температурного напору тратиться на подолання його термічного опору. Тому при одному і тому ж тепловому потоці перегрів рідини, що кипить на окисленій поверхні труби, буде меншим, ніж при кипінні на поверхні чистої труби. Зменшення перегріву рідини у пристінному шарі неминуче тягне за собою зменшення a. З іншого боку плівка окислів підвищує шорсткість труби і це інтенсифікує теплообмін. При низьких теплових потоках домінуючий вплив чинить другий фактор, який обумовлює більш високі значення a_ок у порівнянні з a_ч. Зі збільшенням теплового потоку вплив шорсткості труби зменшується, у той час як негативний вплив термічного опору шару накипу зростає. Тому при великих теплових потоках a_ч оказується значно вищим за a_ок.

Необхідно мати на увазі, що графіком, наведений на рис.24.15, значення коефіцієнта тепловіддачі при кипінні води можна визначати тільки у тій області режимних параметрів, де швидкість суміші не впливає на інтенсивність теплообміну.