




6.2.3. Теплообмін на криволінійній поверхні
При обтіканні криволінійної поверхні внаслідок деформації ліній току виникає повздовжній градієнт тиску і за певних умов (в області сповільненого руху рідини) відбувається відрив пограничного шару від поверхні обтікання. Відрив пограничного шару супроводжується зворотною течією в пограничному шарі і його значне потовщення. При цьому за точкою відриву, вниз за течією, рівняння пограничного шару втрачають свою силу.
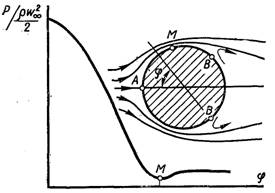
Рис.6.10.Схема обтікання кругового циліндра
Для того щоб пояснити явище відриву, розглянемо обтікання кругового циліндра (рис.6.10). Починаючи з лобової точки А тиск на зовнішній границі пограничного шару зменшується, при цьому, згідно рівняння Бернуллі, швидкість зростає до точки М, де градієнт тиску стає рівним нулю. Далі в області сповільненої течії (др/дх > 0) відбувається поновлення тиску. Але із-за наявності сил тертя у пограничному шарі кінетична енергія частинок рідини оказується недостатньою, щоб подолати підвищення тиску від точки мінімуму тиску до задньої критичної точки, і частинки рідини, які знаходяться безпосередньо біля стінки, спочатку зупиняються, а далі починають рухатися назад, виштовхуючи пограничний шар до зовнішньої течії.
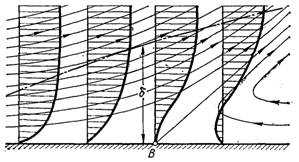
Рис.6.11. Схематичне зображення течії у пограничному шарі біля точки відриву
Картина ліній току в пограничному шарі біля точки відриву В наведена на рис.6.11. У точці відриву пограничного шару градієнт повздовжньої швидкості на поверхні
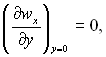 (6.110)
(6.110)
а значить, і локальна величина коефіцієнта тертя нульова.
Розглянуте явище відриву потоку при зовнішньому обтіканні спостерігається також і при течії рідини в каналах, що різко розширюються.
Як уже говорилося, рівняння пограничного шару залишаються справедливими тільки до точки відриву, тому, перед тим як переходити до розрахунку теплообміну на криволінійній поверхні, необхідно визначити параметри точки відриву шляхом інтегрування рівнянь пограничного шару з урахуванням умов (6.110).
Наближені розрахунки показують, що відрив ламінарного ізотермічного пограничного шару відбувається при критичному значенні формпараметра, який входить у рівняння (6.49):
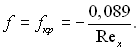 (6.111)
(6.111)
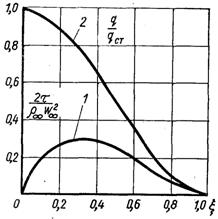
Рис.6.12. Розподіл дотичних напруг (1) і теплових потоків (2) у точці відриву пограничного шару
Розглянемо тепер вплив градієнта тиску на теплообмін. Як ілюстрація на рис.6.12 наведені розподіли теплових потоків і дотичних напружень в перерізі пограничного шару (x = у/d) у точці відриву ламінарного пограничного шару. Як видно з графіка, градієнт тиску не чинить суттєвого впливу на розподіл теплових потоків у перерізі пограничного шару. Тому варто чекати, що і закон теплообміну повинен мати значну консервативність по відношенню до зміни градієнта тиску на зовнішній границі пограничного шару. Такі міркування підтверджуються прямими розрахунками. Значення величини
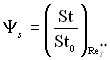
у точці відриву ламінарного пограничного шару з постійними фізичними властивостями і числом Pr = 1 наведені Кутателадзе
dТ/d |
1,0 |
1,25 |
1,5 |
2,0 |
|
0,62 |
0,81 |
0,86 |
1,23 |
Результати розрахунку підтверджують, що повздовжній градієнт тиску чинить малий вплив на відносний закон теплообміну, тому під час інженерних розрахунків впливом градієнта тиску на відносний закон теплообміну зазвичай нехтують і вважають, що
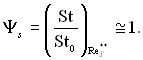 (6.112)
(6.112)
У випадку довільного розподілу швидкості на зовнішній границі пограничного шару розподіл значень коефіцієнтів тепловіддачі можна наближено визначити за допомогою інтегрального метода. Інтегральне співвідношення енергії пограничного шару (6.63) нестислої рідини при обтіканні непроникливої поверхні
![]()
для симетричної відносно осі течії
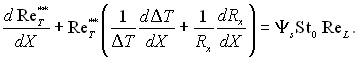
Приймаючи Ys = 1 і підставляючи у цей вираз значення
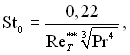 (6.113)
(6.113)
знайдене внаслідок точного розв’язку, отримаємо лінійне диференціальне рівняння відносно числа ![]()
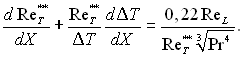
Для випадку течії симетричної відносно осі
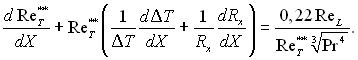
У загальному випадку DТ, ReL і Rx є заданими функціями від х. Інтеграл цього диференціального рівняння при граничних умовах х = 0; ![]() = 0 дорівнює:
= 0 дорівнює:
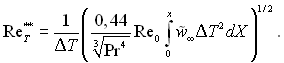 (6.114)
(6.114)
Для випадку течії симетричної відносно осі
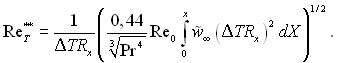
У цих рівняннях Re0 = rҐw0ҐL/m0 – число Рейнольдса, розраховане за швидкістю набігаючого потоку w0Ґ; ![]() = wҐ /w0Ґ – відносна швидкість на зовнішній границі пограничного шару.
= wҐ /w0Ґ – відносна швидкість на зовнішній границі пограничного шару.
Підставивши отримане значення числа ![]() у рівняння (6.113) знайдемо значення локальних чисел St, а значить, і розподіл локального значення коефіцієнта тепловіддачі вздовж поверхні, що обтікає потоком, аж до точки відриву.
у рівняння (6.113) знайдемо значення локальних чисел St, а значить, і розподіл локального значення коефіцієнта тепловіддачі вздовж поверхні, що обтікає потоком, аж до точки відриву.
Якщо необхідно визначити розподіл температури стінки при заданому законі розподілу теплового потоку qcm(x), то інтегральне співвідношення енергії (6.63) для випадку непроникливої стінки можна записати в наступному виді:
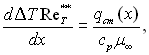
звідки
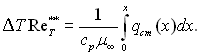
Виразивши число![]() через St по рівнянню (6.113), після нескладних перетворень отримаємо:
через St по рівнянню (6.113), після нескладних перетворень отримаємо:
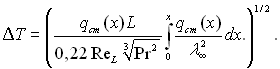 (6.115)
(6.115)
Спів ставимо результати розрахунків теплообміну за наближеним методом і точним автомодельним рішенням. Як було показано, існують автомодельні рішення теплового пограничного шару для наступних граничних умов:
wҐ = Cxm, Tcm = TҐ + axg.
Підставивши ці значення у рівняння (6.114), знайдемо
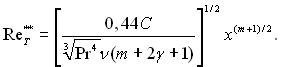 (6.116)
(6.116)
Вираз для числа Стентора отримуємо, підставляючи залежність (6.116) у (6.113)
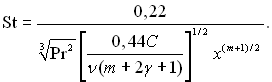 (6.117)
(6.117)
Для параметра NuxRex–1/2 маємо
![]() (6.118)
(6.118)
На рис.6.9 співставленні результати розрахунку параметра NuxRex–1/2 за формулою (6.118) з точними автомодельними рішеннями. Варто відмітити задовільну відповідні сит наближеного рішення з точним за всією областю зміни параметрів g і bў = 2т/(т +1). З рівняння (6.118) виходить, що коефіцієнт тепловіддачі дорівнює нулю за умови
![]() (6.119)
(6.119)
що співпадає з точним розв’язком (див. табл.6.6).
Для відносного коефіцієнта тепловіддачі отримуємо просу формулу
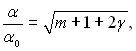 (6.120)
(6.120)
де a0 – значення коефіцієнта тепловіддачі для випадку обтікання плоскої пластини з постійною температурою стінки (т = 0, g = 0), розрахованого по формулі
![]()
при цьому Rex = wҐx/n визначається за швидкістю на зовнішній границі пограничного шару вданому перерізі. Аналогічні результати можна отримати і для коефіцієнтів масообміну. Так для випадку wҐ = Cxm, Сcm = СҐ + axg маємо
![]() (6.121)
(6.121)
де b0 – коефіцієнт масовіддачі.
Для випадку обтікання симетричного відносно осі тіла при ![]()
![]()
![]() маємо
маємо
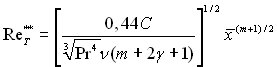
і
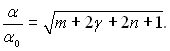
6.2.4. Теплообмін при надзвукових швидкостях руху газу
Температура гальмування. При досягненні швидкості потоку, спів розмірної зі швидкістю звуку, тобто коли
![]()
зменшення швидкості в межах пограничного шару за рахунок гальмівної дії сил тертя тягне за собою значне підвищення температури біля поверхні тіла. При цьому виникає необхідність урахування взаємного впливу температурного і динамічного пограничних шарів.
Повна ентальпія адіабатно загальмованого газу за першим законом термодинаміки визначається залежністю
![]()
Враховуючи, що для ідеального газу ентальпія є функцією тільки температури h = cpT, то можна отримати вираз для температури гальмування Т* = Т + + w2Ґ/(2ср), який можна перетворити до наступного виду:
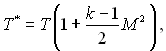 (6.122)
(6.122)
тому що для ідеального газу швидкість розповсюдження звукових коливань визначається формулою
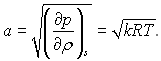
Рівняння (6.122) дозволяє оцінити підвищення температури внаслідок ізоентропійного гальмування. Так для повітря (k ~ 1,4) при М = 1 Т* = 1,2Т, а при М = 6 Т* = 7,2Т, тобто температура ізоентропійного гальмування потоку при М = 6 у сім разів перевищує термодинамічну температуру руху газу.
Подальше підвищення швидкості потоку призводить до надмірно сильного підвищення температури, що тягне за собою виникнення в пограничному шарі хімічних реакцій (дисоціації і іонізації). Це стосується області гіперзвукових течій.
Але, як говорилося раніше, навіть в області надзвукових течій (для повітря М Ј 6) підвищення температури у пограничному шарі за рахунок гальмування дуже велике і значення фізичних параметрів (особливо в’язкості і теплопровідності) вже не можна вважати постійними у пограничному шарі.
Коефіцієнт відновлення. При обтіканні поверхні потоком газу великої швидкості біля поверхні виділяється значна кількість теплоти за рахунок дії сил тертя. Якщо поверхня адіабатно ізольована, то виділена теплота може відводитися від поверхні тіла тільки за рахунок теплопровідності газу. У стаціонарному стані настає рівновага між виділенням і відведенням теплоти. Температуру, яка приймає поверхня за цих умов, називають адіабатною температурою стінки Т*ст..
Відношення різниці температур повністю ізоентропійно загальмованого газу Т*Ґ – ТҐ до дійсної різниці температур Тст.– ТҐ називається коефіцієнтом відновлення
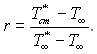 (6.123)
(6.123)
Польгаузен аналітично розрахував коефіцієнт відновлення при повздовжньому дозвуковому обтіканні пластини у випадку ламінарної течії у пограничному шарі. Отримані ним результати можна апроксимувати залежністю
![]() (6.124)
(6.124)
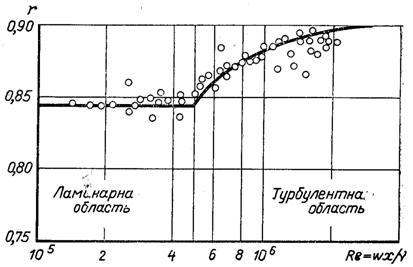
Рис.6.13.Коефіцієнт відновлення пластини, яка поздовжньо обтікає газом при М < 1: точками позначені дослідні дані, суцільною лінією – узагальнююча крива (6.124)
Залежність (6.124) погоджується з дослідними даними. На рис.6.13 співставленні дослідні дані для повітря з теоретичними значеннями розрахованими по залежності (6.124).
Розрахунки і дослідні дані виконані для ламінарної області течії зі швидкістю, яка перевищує швидкість звуку, показують, що залежність коефіцієнта відновлення від числа Прандтля залишається тією ж.
На рис.6.24 наводяться результати дослідів Ебера, отримані ним при обдуванні конусів надзвуковим потоком, які надійно погоджуються з теоретичною формулою (6.124).
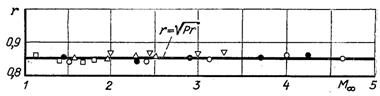
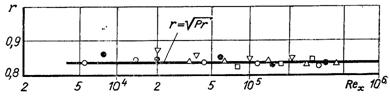
Рис.6.14. Дослідні значення коефіцієнтів відновлення r для ламінарного пограничного шару на конусах з різним кутом при вершині: точками позначені дослідні дані, суцільною лінією – узагальнююча крива (6.124)
Аналітичний розв’язок можна отримати і для тіл, які мають погано обтічну форму. Якщо у випадку ламінарного характеру течії у пограничному шарі коефіцієнт відновлення віднести до параметрів на зовнішній границі пограничного шару (рис.6.15), то отримані таким чином локальні значення коефіцієнта відновлення raт аж до точки відриву задовільно описується залежністю ![]() що також свідчить про консервативність процесу відновлення ентальпії при зміні повздовжнього градієнту тиску.
що також свідчить про консервативність процесу відновлення ентальпії при зміні повздовжнього градієнту тиску.
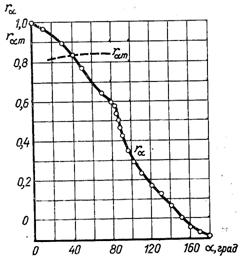
Рис.6.15. Розподіл значень коефіцієнта відновлення ra і ram по колу циліндра, який поперечно обтікає:
МҐ = 0,685; ReҐ = 1,05·105; a – центральний кут
При числах Pr = 1, як було показано раніше, при подібності граничних умов спостерігається подібність полів швидкості і температури гальмування:
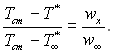
Ця умова точно виконується при повздовжньому обтіканні пластини з постійною температурою стінки необмеженим потоком.
Для газів, у яких числа Прандтля мало відрізняються від одиниці, в основу зв'язку між розподілом температур і швидкостей можна покласти наведене вище співвідношення, надавши йому наступного вигляду:
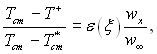 (6.125)
(6.125)
де ε(ξ) – коефіцієнт неподібності полів температури і швидкості; Т+ – розрахункова температура:
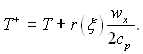 (6.126)
(6.126)
Вид функції ε(ξ), r(ξ) в загальному випадку залежить від градієнту тиску, неізотермічності, масообміну.
На стінці wx = 0, T+ = T*cm, r(ξ) = r. Як відмічалося раніше, коефіцієнт поновлення r для газів близький до одиниці, тому в достатній мірі точності можна вважати, що r(ξ) = r. Тоді співвідношення (6.126) можна переписати:
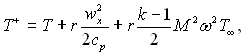 (6.127)
(6.127)
де ω = wx/w∞, M =w∞/a.
Приймаючи до уваги рівняння (6.125), (6.127), а також вираз для коефіцієнта поновлення (6.123), співвідношення між розподілом температур і швидкостей (6.125) можна отримати в наступному виді:
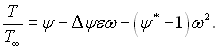 (6.128)
(6.128)
У цьому рівнянні 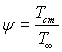 – температурний фактор;
– температурний фактор; 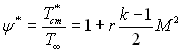 –
кінетичний температурний фактор;
Δψ = ψ – ψ*
– фактор теплообміну. При
Δψ
< 0
тепловий потік спрямований до поверхні; при
Δψ
> 0 поверхня віддає теплоту потоку.
–
кінетичний температурний фактор;
Δψ = ψ – ψ*
– фактор теплообміну. При
Δψ
< 0
тепловий потік спрямований до поверхні; при
Δψ
> 0 поверхня віддає теплоту потоку.
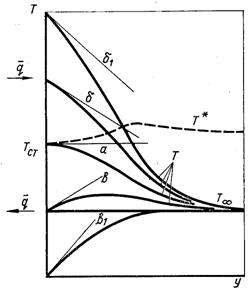
Рис.6.16. Криві розподілу температури в ламінарному пограничному шарі на пластині при високих швидкостях: а – теплообмін відсутній; б,б1 – при Тст>T*cm і напрямку теплового потоку від стінки; в,в1 – тепловий потік спрямований до стінки
Як тільки температура обтічної поверхні Тст відхиляється від адіабатної температури стінки Т*ст., між поверхнею і потоком розпочинається процес теплообміну. На рис.6.16 наведені криві розподілу температур в ламінарному пограничному шарі у потоці газу великої швидкості. З рисунка видно, що коефіцієнт тепловіддачі необхідно визначати за різницею між дійсною температурою поверхні Тст і адіабатною температурою стінки Т*ст., тобто
![]()
У цьому випадку при qcm→ 0, Tcm – T*cm → 0, а коефіцієнт тепловіддачі, що характеризує інтенсивність конвективного теплообміну і залежить від гідродинаміки потоку, зберігає кінцеве значення αе. В окремому випадку дозвукових швидкостей Т*ст→ Т∞ і залишається звичайне визначення коефіцієнта тепловіддачі.
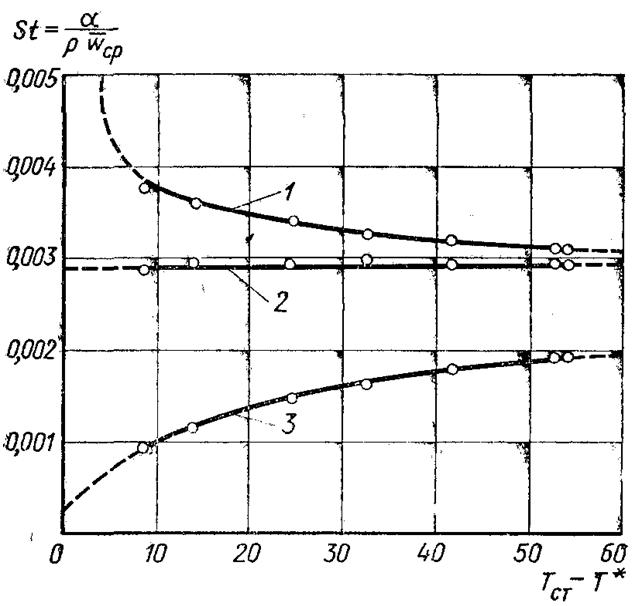
Рис.6.17. Коефіцієнти тепловіддачі, які відповідають різним визначенням, при течії повітря в трубі для М < 1 (за Мак-Адамсоном, Ніколаї, Кінану): 1 – q=α0(Tcm–T*cm); 2 – q=αe(Tcm– –T*cm); 3 – q=α(Tcm–T*cm)
На рис.6.17 наведені результати дослідів Мак-Адамса та ін., які стосуються тепловіддачі в трубі при великих швидкостях течії газу. Ці результати стверджують правильність вибору величини теплового напору ΔТ = Tcm – T*cm. У цьому випадку коефіцієнт тепловіддачі практично не залежить від температурного напору. Крім цього, наведені результати показують, що при великих температурних напорах за температурний напір можна вибирати величину ΔТ = Tcm – T*cm, що дуже зручно, тому що відпадає необхідність у визначенні коефіцієнта поновлення.
● Перетворення рівнянь стисливого пограничного шару. Цей метод дозволяє привести рівняння до форми близької до рівнянь для нестисливої рідини. Перетворення координат значно спрощує розрахунок стисливого пограничного шару і дозволяє використовувати надійно опрацьовані методи (як точні, так і інтегральні) розрахунку рівнянь нестисливого пограничного шару.
Повна система диференціальних рівнянь плоского стисливого пограничного шару у випадку обтікання непроникливої пластини має вигляд:
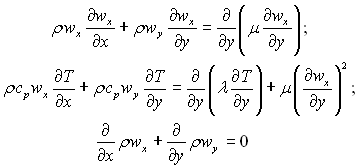
з граничними умовами y=0 wx=0, T=Tcm; y=∞ wx=w∞, T=T∞. Наслідуючи Дородіцину, який вперше запропонував розглядуваний метод, введемо нові перемінні
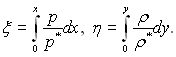
У цих залежностях р* і ρ* – відповідно тиск і густина адіабатно загальмованого газу.
Замінимо для випадку обтікання плоскої пластини р* і ρ* на р∞ і ρ∞ – тиск і густину на зовнішній межі пограничного шару, тоді попередні співвідношення набудуть вид
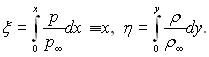 (6.129)
(6.129)
тому що р=р∞ по причині сталості тиску поперек пограничного шару.
Перехід від диференціювання по х і у до диференціювання по ξ і η здійснюється за формулами
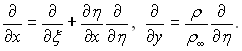 (6.130)
(6.130)
Використовуючи співвідношення (6.130), можна перетворити рівняння руху, попередньо скоротивши на ρ:
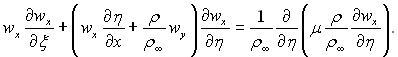
Перетворимо тепер рівняння нерозривності потоку і представимо його у виді:
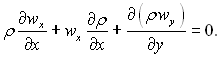 (6.131)
(6.131)
Виконаємо диференціювання другого рівняння (6.129) спочатку по х при постійному значенні у, а далі по η, знайдемо
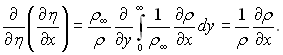
Підставимо отриманий вираз в рівняння (6.131) і перейдемо до нових перемінних ξ і η, отримаємо
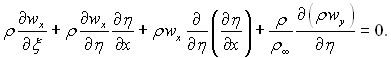
Цей вираз можна перетворити до наступного виду:
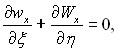
де 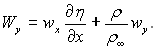
Таким чином, перетворені рівняння руху і нерозривності потоку у випадку обтікання непроникливої пластини приймають вид:
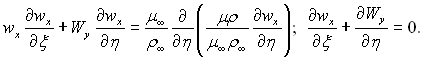 (6.132)
(6.132)
У випадку лінійної залежності в’язкості від температури, тобто коли μρ=μ∞ ρ∞, рівняння (6.132) за своїм видом повністю співпадають з відповідними рівняннями для нестисливої рідини.
Тепер для вирішення динамічної задачі можна використати розглянутий нами метод.
Введемо, згідно визначенню, функцію току ψ, яка задовольняє рівняння нерозривності потоку:
![]()
Рівняння руху при цьому набуває наступного вигляду
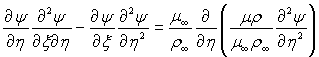 (6.133)
(6.133)
з граничними умовами: при η=0 ψ=0, дψ/дη=0; при η=∞ дψ/дη=w∞. Введемо, як і раніше, перемінні Блазіуса, які визначаються рівняннями:
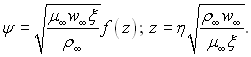
Вважаємо, що функція f(z) залежить тільки від z, тоді похідні функції току мають вигляд:
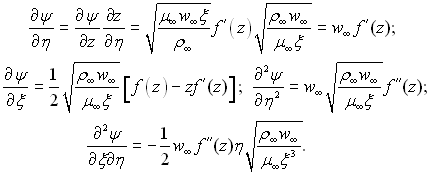
Підставимо значення похідних у рівняння руху (6.133), після спрощення отримаємо
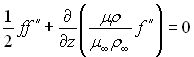 (6.134)
(6.134)
з граничними умовами: при z = 0 f = 0; при z = ∞ f ′= 1.
Аналогічним чином за допомогою перемінних Дородіцина рівняння енергії можна привести до вигляду:
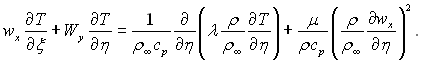
Після введення перемінних Блазіуса і нескладних перетворень, получимо
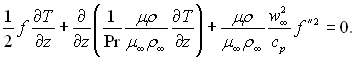
Відмітимо, що 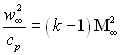 , і вважаючи число Pr постійним, що з достатньою точністю виконується для газів внаслідок однакової залежності в’язкості і теплопровідності від температури, отримаємо в кінцевому виді:
, і вважаючи число Pr постійним, що з достатньою точністю виконується для газів внаслідок однакової залежності в’язкості і теплопровідності від температури, отримаємо в кінцевому виді:
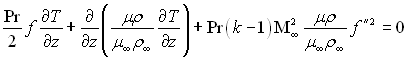 (6.135)
(6.135)
з граничними умовами, які можна виразити в одній з наступних форм:
Інтегрування рівнянь (6.134) і (5.135) в загальному випадку вимагає застосування числових методів, але у випадку лінійної залежності в’язкості від температури названі рівняння приймають форму рівнянь, справедливих для нестисливої течії.
Дійсно, якщо зв’язок між в’язкістю задається в вигляді степеневої залежності від температури
![]()
і, згідно рівнянню стану ідеального газу,
![]()
то при лінійній залежності в’язкості від температури (п = 1)
μρ = μ∞ρ∞.
Таким чином, з урахуванням цієї рівності рівняння руху приймає вид
![]()
Як бачимо, що у цьому випадку рівняння руху автономне і нічим не відрізняється від відповідного рівняння для нестисливої рідини, виходячи з цього для визначення функції f і її похідних можна використовувати дані наведені в табл.6.2.
Аналогічним чином для випадку лінійної залежності в’язкості від температури можна привести рівняння енергії до форми, яка відповідатиме течії нестисливої рідини, якщо ввести нову перемінну для температури:
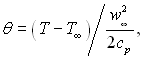
![]() (6.136)
(6.136)