6.2.5. Точне рішення рівняння енергії пограничного шару стисливого газу при др/дх = 0 і лінійній залежності в’язкості від температури

● Випадок теплоізольованої стінки. Рівняння енергії, записане у формі (6.136), представляє собою звичайне диференціальне рівняння, яке можна розв’язати методом варіації постійних чи за допомогою введення інтегрального множника. Відшукаємо спочатку окреме вирішення цього рівняння для випадку теплоізольованої стінки: θ(∞) = 0, θ′(0) = 0. Позначимо цей розв’язок через θ_ад, отримаємо за допомогою названого методу наступний вираз:

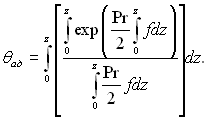(6.137)

Використовуючи значення f, розраховане раніше, рівняння (6.137) можна інтегрувати числовими методами. Отримані результати в діапазоні чисел Pr=0,5...10 апроксимуються залежністю θ_ад = Pr^1/2. Зауважимо, що дорівнює раніше виведеному коефіцієнту поновлення. Отримане значення погоджується з експериментальними даними.

● Теплообмін при помірній швидкості. Рівняння енергії (6.136) у цьому випадку значно спрощується, тому що при М → 0 зникає член, який враховує дисипацію енергії. У випадку лінійної залежності в’язкості від температури рівняння енергії приймає вид, який точно співпадає з рівнянням енергії і справедливий для течії з постійними фізичними властивостями, якщо в останньому Т замінити на J за рівнянням (6.78):

де J = (Т_ст – Т)/(Т_ст – Т_∞). Рішення цього рівняння було отримане раніше.

Густину теплового потоку на стінці знайдемо з рівняння

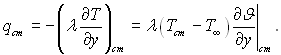
Переходячи до перемінних z і η, знайдемо

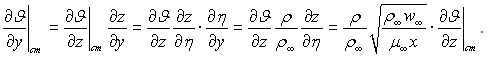
Похідну було знайдено раніше [див.(6.86)]. З урахуванням цього вираз для густини теплового потоку набуває вигляду

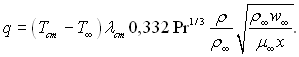
Переходячи до локальних значень числа Нуссельта, отримаємо

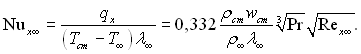
і, на кінець, вважаючи, що теплопровідність знаходиться в тому ж співвідношенні з температурою, що і динамічна в’язкість при п = 1, знаходимо кінцеве значення числа Нуссельта:

Отже, рішення, отримане для пластини, яку обтікає потік зі сталими фізичними властивостями, справедливе і для перемінних властивостей, якщо фізичні параметри, що входять до безрозмірних комплексів, відносити до температури на зовнішній поверхні пограничного шару. У цьому разі відбувається взаємна компенсація впливу фізичних властивостей на закон теплообміну.

● Теплообмін при великій швидкості. Для знаходження розв’язку рівняння енергії за наявністю теплообміну, необхідно яке-небудь частинне рішення додати до загального рішення однорідного рівняння:

Таким способом отримано рішення:

(6.138)

де 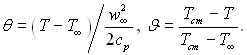Сталі С₁ і С₂ визначаються з граничних умов: z = 0 θ = θ_cm; z = ∞ θ = 0. З першої граничної умови виходить, що С₁ = –С₂; з другої

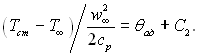
Підставимо визначені значення констант в рівняння (6.138), після нескладних перетворень знайдемо розподіл температури в такому виді:

(6.139)

Густину теплового потоку знайдемо з рівняння

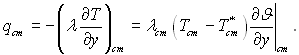
Виконавши такі ж перетворення, як і в попередньому випадку обтікання потоком нестисливої рідини з перемінними фізичними властивостями, знайдемо вираз для локального значення числа Нуссельта у такому виді:

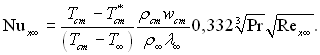
При лінійній залежності теплопровідності від температури отримаємо

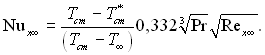(6.140)

В останніх рівняннях Т^*_ст. характеризує вплив числа М на тепловіддачу. Якщо, як було показано вище, коефіцієнт тепловіддачі відносити до різниці температур (Т_ст – Т^*_ст), то прийдемо до аналогічної залежності, отриманій раніше для течії нестисливої рідини з постійними фізичними властивостями.

6.2.6. Наближений метод розв’язку за допомогою інтегрального співвідношення енергії

Аналіз точних рішень для пластини при лінійній залежності в’язкості і теплопровідності показує, що вплив зміни фізичних властивостей газу може взаємно компенсуватися.

Тому рішення, отримані для випадку течії з постійними фізичними властивостями, зберігають свою силу і для течій зі змінними властивостями в широкому діапазоні зміни температурного фактора ψ=Т_ст/Т_∞, і в інженерних розрахунках впливом неізотермічності при малих швидкостях течії зазвичай нехтують.

Ці міркування підтверджуються результатами більш точних розрахунків. Рядом дослідників виконані розрахунки шляхом числового інтегрування деяких випадків автомодельних течій (течія біля клину, поблизу критичної точки циліндра). При цьому використовувалися залежності фізичних констант від температури, близькі до реальних, апроксимуючі зміни фізичних властивостей повітря в широкому діапазоні зміни температури (300...1300 °С). Ці розрахунки показують, що, по-перше, вплив перемінних фізичних властивостей можна врахувати виразом

при цьому порівняння чисел St виконується за умови Re_x =idem, і, по-друге, ця залежність закону теплообміну дуже слабка, навіть у випадку

Так, наприклад, при w_∞ – const (пластина, клин) п = –0,01 при ψ > 1; n = 0 при   ψ < 1.

Розв’язок рівняння енергії стисливого пограничного шару при др/дх = 0, Pr = 0,7 виконано Ван-Дрійстом методом послідовних наближень.

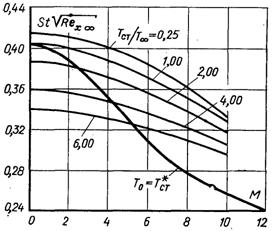
Рис.6.18. Теплообмін в ламінарному високошвидкісному пограничному шарі повітря (за Ван-Дрістом)

Результати розрахунку наведені на рис.6.18. Можна замітити, що число St зменшується зі збільшенням числа М. Ці результати апроксимуються залежністю

(6.141)

де ψ^* = Т^*_ст./Т_∞._./Т_∞.

Рівняння (6.141) справедливе при ψ>1 і М ≤ 6. При співставленні чисел St по числу Re_Т^** залежність (6.141) приймає вид

(6.142)

Як було показано, рівняння енергії стисливого пограничного шару записується у формі (6.60), якщо число Re_T^** відносити до динамічної в’язкості μ_0∞, яка визначається за температурою гальмування незбуреного потоку. Число St₀ у цьому випадку розраховується за формулою

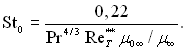
Таким чином, за аналогією з (6.114), інтеграл рівняння енергії можна записати в наступному вигляді

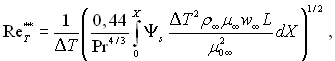
де Ψ_s визначається за рівнянням (6.142). Величину 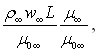яка входить під знак інтеграла, можна перетворити до наступного виду:

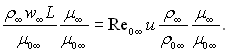
Тут число 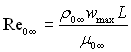не залежить від Х і може бути винесене з-під знака інтеграла; де максимально можлива швидкість течії; густина при температурі гальмування не подразненого потоку.

Маючи на увазі розглянуте перетворення, отримаємо кінцевий вираз

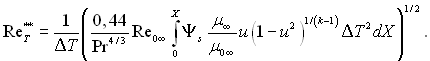(6.143)

Якщо заданий закон розподілу теплових потоків q_cm(x), то розрахунки виконуються за формулою

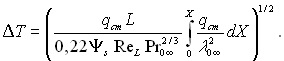(6.144)

У цьому випадку, як і в попередньому Ψ_s визначається за формулою (6.142).

6.2.7. Тертя і теплообмін на проникливій поверхні

Система рівнянь пограничного шару (6.65) для течії нестисливої рідини з постійними параметрами і граничними умовами при у = 0 w_x = 0, w_y = w_cm; при y = _∞ w_x = w_∞ має автомодельне рішення.

Рис.6.19. Повздовжнє обтікання пластини з рівномірно розподіленим відсмоктуванням

Розглянемо обтікання плоскої наполовину обмеженої пластини потоком нестисливої рідини при наявності рівномірного відсмоктування газу з пограничного шару (рис.6.19).

У цьому випадку є автомодельне рішення, для якого розподіл швидкостей не залежить від біжучої довжини х.

При дw_x/дх = 0 з рівняння нерозривності потоку слідує w_y=w_cm= const і рівняння руху набуває вигляду

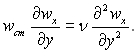
Розв’язок цього рівняння:

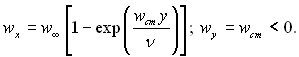(6.145)

Для товщини витіснення і товщини втрати імпульсу маємо

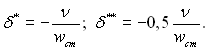(6.146)

Дотичні напруження на стінці і коефіцієнт тертя визначаються наступними формулами:

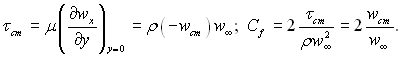(6.147)

Як видно з формули, дотичні напруження в розглядуваних умовах не залежать від в’язкості рідини.

Визначимо параметр проникливості 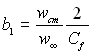для даного випадку при b₁ = –1.

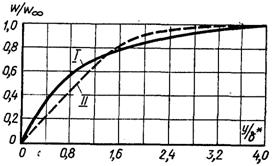
Рис.6.20. Розподіл швидкостей в пограничному шарі на плоскій пластині: І – асимптотичний профіль швидкостей за рівномірно розподіленому відсмоктуванні; ІІ – профіль швидкостей без відсмоктування

На рис.6.20 співставленні профілі швидкостей на проникливій пластині [за рівнянням (6.145)] і на непроникливій пластині. Як видно з графіка, відсмоктування рідини з пограничного шару робить профіль більш заповненим. Автомодельний розподіл швидкостей типу (6.145) практично установлюється зі значень повздовжньої координати х, яка визначається формулою

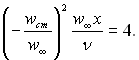
Відносний закон тертя для розглядуваних умов визначається з рівнянь (6.147), (6.146) і (6.213):

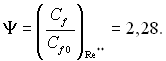(6.148)

Таким чином, закон тертя за асимптотичного відсмоктування в координатах Ψ=f(b₁) відповідає одній точці (b₁ = –1, Ψ=2,28). Відповідно

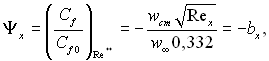(6.149)

де .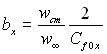

Аналогічним чином можна отримати автомодельне рішення рівняння енергії. За умови, що дТ/дх = 0 рівняння енергії набуває вид

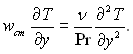(6.150)

Рішення цього рівняння:

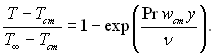(6.151)

З урахуванням того, що 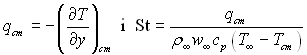отримуємо

(6.152)

Для проміжних областей значення b₁ можна приймати лінійну залежність для закону теплообміну, тобто

.

Таким чином, коефіцієнт тепловіддачі при асимптотичному відсмоктуванні газу дорівнює відносним витратам газу через поверхню і збільшується в порівнянні з непроникливою поверхнею. Відсмоктування газу з пограничного шару використовують для запобігання відриву пограничного шару внаслідок дії додатного градієнта тиску.

Для багатьох прикладних задач викликає зацікавленість випадок вдування газу через теплообмінну поверхню (випаровування, сублімація, пористе охолодження та ін.).

Визначимо умови, за яких буде існувати автомодельне рішення рівнянь пограничного шару. Для степеневого закону зміни швидкості

(6.153)

звідки

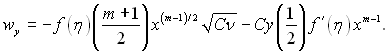(6.154)

На стінці при у = 0, η = 0 і w_y = w_cm, отже,

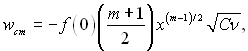(6.155)

чи

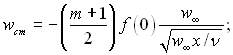(6.156)

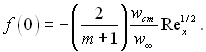(6.157)

Таким чином, для того щоб функція f(0) не залежала від х, необхідно, щоб вдування газу за довжиною змінювалося у відповідності з залежністю

w_cm ~ x^(m–1)/2. (6.158)

В окремому випадку на околиці любої точки (т = 1), w_cm = const. При обтіканні плоскої пластини (т = 0) w_cm ~ x^–0,5.

Рішення рівняння енергії у вигляді (6.82) справедливе і для розглядуваних умов, тільки функцію f(η) необхідно брати з розрахунку динамічного пограничного шару для проникливої поверхні.

Таблиця 6.6. Значення Nu_xRe_x^–1/2 в ламінарному пограничному шарі

(Тст, Т_∞, w_∞ постійні) при різних значеннях b і Pr

Таблиця 6.7. Значення Nu_xRe_x^–1/2 в ламінарному пограничному шарі

(Т_ст, Т_∞ постійні Pr = 0,7 ) при різних значеннях b і m

Результати розрахунків теплового пограничного шару на проникливій поверхні при різних значеннях параметра проникливості 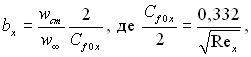наведені в табл.6.6 і 6.7, показують, що вдування газу в пограничний шар призводить до різкого зменшення коефіцієнта тепловіддачі. Для випадку обтікання плоскої пластини при параметрі вдування

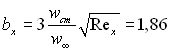
настає відтиснення пограничного шару від стінки і коефіцієнт тепловіддачі стає рівним нулю.

У випадку вдування стороннього газу до рівнянь руху, нерозривності потоку і енергії необхідно добавити рівняння дифузії газу, що вдувається. Повна система рівнянь стисливого двокомпонентного пограничного шару має такий вигляд:

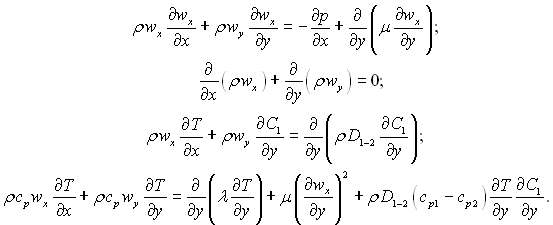(6.159)

У цих рівняннях С₁ = ρ₁/ρ – масова частка газу, що вдувається; D_1-2 – коефіцієнт дифузії.

З граничними умовами: при у = 0 w_x = 0, w_y = w_cm, T = T_cm; при у = ∞ w_х = w∞, T = T∞, С₁ = 0.

Концентрація газу, що вдувається, на стінці визначається з рівняння балансу маси на поверхні теплообміну, яке для наполовину проникливої стінки має вид

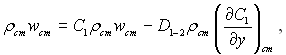(6.160)

звідки

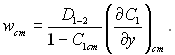(6.161)

Система диференціальних рівнянь (6.159) розв’язана для деяких окремих випадків. Так, Еккерт і Хартнет рішили цю систему для випадку обтікання пластини потоком нестисливої рідини з постійними фізичними властивостями. При цьому вважалося, що властивості компонентів не залежать від тиску і температури і мало відрізняються один від іншого.

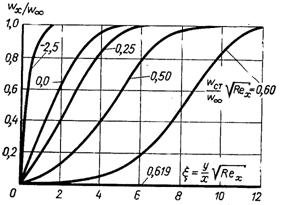
Рис.6.21. Розвиток безрозмірного профілю швидкості в ламінарному пограничному шарі в залежності від параметра вдування

На рис.6.21 і 6.22 наведені розподіли швидкості, температури і концентрації в залежності від параметра вдування 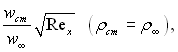який однозначно зв’язаний з раніше введеним фактором проникливості стінки

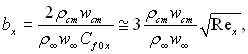
де

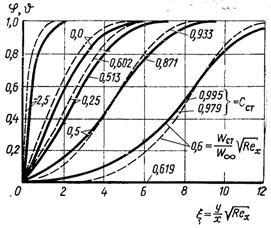
Рис.6.22. Безрозмірні профілі температури і концентрації в ламінарному пограничному шарі для різних параметрів вдування при числах Прандтля (–––––– – Pr = Sc = 0,7; ------ – Pr = Sc = 1,0)

Аналіз графіків, наведених на рис.6.21 і 6.22, показує, що з і збільшенням значення параметрів вдування пограничний шар товщає, а при досягненні 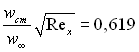(що відповідає b_x = b_кр≈ 1,86) відбувається відтискування пограничного шару від поверхні обтікання.

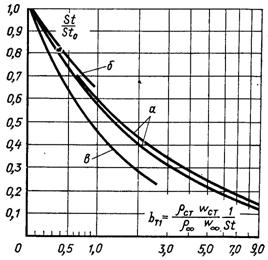
Рис.6.23. Теплообмін при ламінарному пограничному шарі з вдуванням і постійною швидкістю зовнішньої течії: а – при постійних фізичних властивостях (Pr = 1; 0,7); б – при змінних фізичних властивостях і вдуванні СО₂ в потік повітря (Pr = 0,73; Sc = 1,04); в –– при змінних фізичних властивостях і вдуванні Не в потік повітря (Pr = 0,73; Sc = 0,23)

На рис.6.23 наводяться результати числових розрахунків теплообміну на пластині, виконані Бароном, при вдуванні гелію і диоксиду вуглецю в ламінарний пограничний шар повітря. Там же нанесена крива при вдуванні однорідного газу. Можна замітити, що при вдуванні “легких” газів ефективність теплового захисту зростає. Це обумовлено в основному впливом питомої теплоємності газу, що вдувається.

Гросс, Хартнет і інші узагальнили результати числових розв’язків рівнянь ламінарного пограничного шару на проникливій пластині і запропонували наступну формулу для розрахунку локального теплообміну:

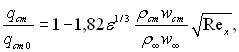
де ε – відношення відносних молекулярних мас газу основного потоку і газу, що вдувається; q_cm0 –тепловий потік на непроникливій пластині при тому ж Re_x.

Фізичні константи, які входять в число Re_x, розраховуються за визначальною температурою:

С.С.Кутателадзе на підставі аналізу вище наведених залежностей запропонував більш зручну форму врахування впливу вдування на відносний закон теплообміну при Re_T^** = idem в такому виді:

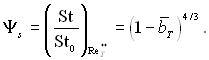(6.162)

Тут відносний фактор проникливості стінки; 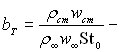тепловий параметр проникливості; St₀ – число Стентора на непроникливій поверхні при наявності числа Re_T^** ;

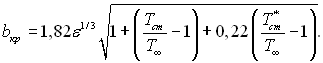(6.163)

Отриманий вираз для відносного закону теплообміну наполовину проникливої пластини можна використати для розрахунку теплообміну наполовину проникливої неізотермічної поверхні з невеликою кривизною, яку обтікає дозвуковий потік. У цьому випадку інтегральне рівняння енергії (6.63) записується так:

У цьому рівнянні , а Ψ_Т – поправка на неізотермічність і стисливість [див.(6.142)].

У загальному випадку при заданих функціях w̃_∞, ΔТ і b_Т  від безрозмірної повздовжньої координати Х і поверхні, яка прониклива за всією довжиною, рішення рівняння енергії відносно Re_T^** має вид

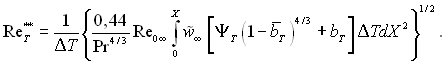(6.164)

Розподіл підводу охолоджувального газу визначаємо за формулою

За визначеними значеннями числа Re_T^** знаходимо розподіл числа St₀ за формулою (6.93).

Локальне значення числа St визначається за виразом

а початкову температуру охолоджувального газу – за відомими витратами

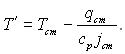
Якщо задана температура стінки, як, наприклад, при випаровуванні чи сублімації матеріалу поверхні, то визначенню підлягає кількість відведеної від цієї поверхні пари.

У цьому випадку витрати пари визначаються рівнянням теплового балансу

У цьому рівнянні r – прихована теплота випаровування (сублімації).

Якщо ввести, як і в попередньому випадку, значення b_T і St в це рівняння, отримаємо

b_T = Ψ_s/К, (6.165)

де К = r/(c_pcmΔT) – число Кутателадзе.

Розв’язуючи разом рівняння (5.162) і (6.165), знаходимо параметр вдування b_T, а далі за рівнянням (6.164) – число Re_T^** і т. д.

Якщо задані параметри зовнішньої течії, температура стінки і початкова температура охолоджувального газу, який надходить через пористу стінку Т′, то витрати охолоджувального газу також визначаться з балансового рівняння

q_cm = j_cmc_pcmΔT′,

де ΔT′ = Т_ст – T′.

Після введення b_T і St отримаємо

(6.166)

Таким чином, спів ставляючи між собою вирази (6.165) і (6.166) побачимо, що для пластини умова b_T = const рівнозначна умові Т_ст = const.