6.2.8. Теплообмін за наявності хімічних реакцій

За наявності хімічних реакцій в пограничному шарі вираз для теплового потоку (без урахування термо- і бародифузії) згідно рівнянню (6.31) набуває вигляду

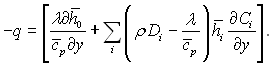(6.167)

Тут – так названа “заморожена” питома теплоємність суміші; – повна ентальпія, яка включає в себе як теплову, так і хімічну енергію; – повна ентальпія гальмування.

Перепишемо рівняння (6.167) по іншому:

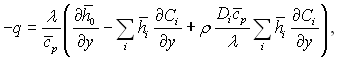
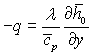отже відносна величина теплової енергії, яка передається двома механізмами, залежить як від співвідношення хімічної і теплової енергії, так і від значення числа Люіса – Семенова Якщо число Le = 1, то незалежно від механізму теплообміну і швидкості хімічних реакцій в суміші. У цьому випадку диференціальне рівняння енергії, записане через повні ентальпії гальмування, не містить в собі швидкості утворення окремих компонентів і має такий же вигляд, як і звичайне рівняння енергії для не реагуючого газу. Отже, у цьому випадку тепловий потік q залежить в основному від різниці повних ентальпій на стінці і в потоці і не залежить від того, де розташована зона хімічних реакцій. Для більшості газових сумішів значення числа Le ~ 1, а переносні властивості слабко залежать від складу суміші, тому таке наближення допустиме. Аналогічне спрощення задачі було вперше використане Швабом і Зельдовичем при дослідженні ламінарного дифузійного полум’я.

● Взаємодія між потоком і матеріалом поверхні. Розглянемо питання взаємодії між реагуючим пограничним шаром і поверхнею. Явища, які нас цікавлять, спільним є одночасне проходження хімічних реакцій в газовій фазі і реакцій між твердою поверхнею і реагуючим пограничним шаром. Але, як відмічалося раніше, навіть у випадку потрійної аналогії, коли Le = Pr = Sc = 1, відсутня подібність між розподілом концентрації, температури і швидкості, якщо розглядати парціальні концентрації компонентів реагуючої суміші.

Якщо ввести повні концентрації для елементів суміші, то можна позбавитися цієї незручності. Зв’язок між С_і і С_k дається виразом

(6.168)

де С_і  – масова частка і-го елемента; r_i,k – масова частка і-го елемента в k-му компоненті; C_k – масова частка k-го компонента.

Тому що С_і  =const, то

(6.169)

Розглянемо течію біля поверхні, матеріал якої інтенсивно випаровується, при цьому пари матеріалу поверхні реагують з нагрітим пограничним шаром, який складається із суміші молекул і атомів кисню і азоту. За цих умов в пограничному шарі одночасно можуть протікати наступні реакції:

Е + О Ђ ЕО; Е + 2О Ђ ЕО₂; E + N Ђ EN;

2E + O₂ Ђ 2EO; E + O₂ Ђ EO₂; 2E + N₂ Ђ 2EN;

O + O Ђ O₂; N + N Ђ N₂.

Тоді у відповідності з рівнянням (6.168) для масових часток О, N і Е матимемо:

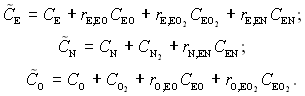(6.170)

Використовуючи співвідношення (6.169), отримаємо для dC_E:

(6.171)

Аналогічні рішення можна отримати для інших масових часток.

Реакції, які відбуваються в пограничному шарі, можуть супроводжуватися чи виділенням теплоти при утворенні компонентів, чи поглинанням теплоти при дисоціації. Зміна ентальпії під час реакції при р = const характеризується тепловим ефектом реакції: ∆Q_p = –∆H. Запишемо реакцію утворення у формі

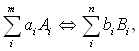
де a_i, b_i – стехіометричні коефіцієнти; А_і, В_і – символи хімічних елементів; тоді

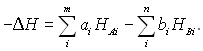(6.172)

Тут Н_Аі – молярна ентальпія А-го хімічного елементу.

Введемо поняття питомої ентальпії, яка визначається з рівняння:

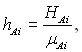
де μ_Аі  – відносна молекулярна маса хімічного елементу А_і.

Питомий тепловий ефект реакції елемента можна отримати з рівняння (6.172) в такому виді:

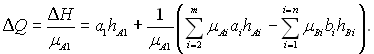(6.173)

Так, для реакції Е + О ? ЕО

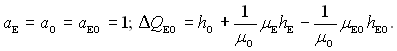
Помножимо і розділимо праву частину отриманої рівності на μ_ЕО (відносну молекулярну масу ЕО) і, зауважимо, що, наприклад, μ_О/μ_ЕО = r_O,EO, знайдемо величину питомого теплового ефекту:

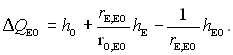(6.174)

Аналогічним чином визначаються питомі теплові ефекти інших реакцій.

Теплоти дисоціації кисню і азоту відповідно рівні:

(6.175)

● Тепловий потік за наявності хімічних реакцій в ламінарному пограничному шарі при Le = 1. Складемо рівняння балансу теплоти на реагуючій поверхні (рис.6.24). Як було показано раніше, до поверхні теплота переноситься шляхом теплопровідності і дифузії:

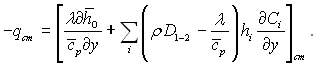
У той же час від поверхні виноситься потік ентальпії (ρw_y)_cmh_cm в пограничний шар, а з боку стінки підводиться потік ентальпії (ρw_y)_cmh_Еcm, де h_cm – повна ентальпія суміші газів на поверхні, h_Еcm – ентальпія поверхні стінки при температурі поверхні.

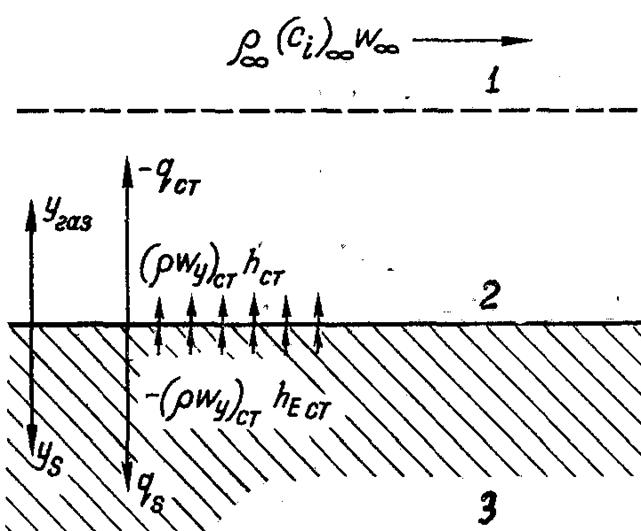
Рис.6.24. Схема теплових потоків на реагуючій поверхні: 1 – межа пограничного шару; 2 – поверхня розділу газ –тверда стінка; 3 – твердий матеріал, що випаровується з поверхні

Якщо знехтувати променевим теплообміном, то отримаємо вираз для сумарного теплового потоку, який проникає в поверхню

Підставляючи в це рівняння вираз для q_cm, отримаємо:

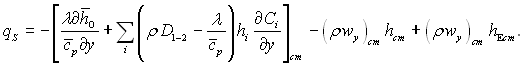(6.176)

Якщо число Le = 1, то

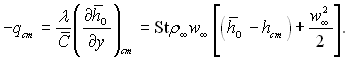
Введемо у вираз (6.176), як і в випадку проникливої стінки, параметр вдування 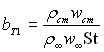і приховану теплоту випаровування поверхні hJ. Так для реакції Е_тв Ђ Е_газ

hJ + h_Eтв = h_Eгаз.

Таким чином, при числі Le = 1 тепловий потік у стінку можна представити у наступному виді:

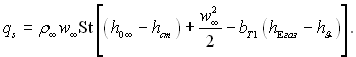(6.177)

За визначенням різниця ентальпій газів суміші запишемо так:

(6.178)

Компонента Е присутня тільки в пограничному шарі, тобто С_Е∞ = О, тому об’єднаємо рівняння (6.177) і (6.178), при цьому отримаємо

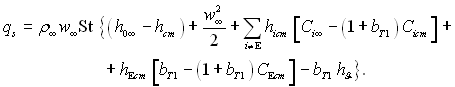(6.179)

Рівняння (6.179) можна записати і через теплові ефекти реакції якщо використати вирази типу (6.174) і (6.175). Спростимо рівняння (6.179), використовуючи граничні умови.

Як було показано у випадку потрійної аналогії (Le = Sc = Pr = 1), диференціальні рівняння енергії і дифузії пограничного шару стають однаковими при введенні повної концентрації, звідки слідує, що при подібності граничних умов існує подібність в розподілі повної енергії гальмування і концентрацій. Так, наприклад, для компоненти О можна написати

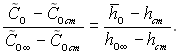(6.180)

На поверхні тіла для любого компонента, крім Е, сумарний потік маси повинен зникати, тобто дифузійний потік маси компоненти повинен дорівнювати конвективному потоку:

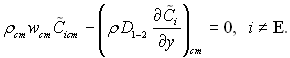(6.181)

Для елемента поверхні сумарний потік маси дорівнює потоку речовини, яка випаровується з поверхні:

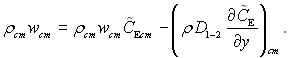(6.182)

Підставивши (6.180) в (6.181) і виконавши диференціювання, отримаємо

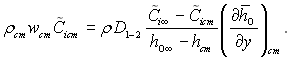
Вводячи до цього співвідношення параметр вдування b_T1 і число St, отримаємо

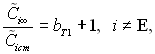(6.183)

де 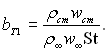І на кінець, підставляючи значення С_і, яке визначається зі співвідношення (6.170), знаходимо

(6.184)

У цьому рівнянні j → O, N; j2 → O₂, N₂.

Аналогічне співвідношення можна отримати і для компоненти Е з урахуванням того, що на зовнішній границі пограничного шару С_Е∞ = 0 рівняння (6.182) набуває вид 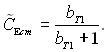(6.185)

Використовуючи співвідношення (6.184), (6.185) і (6.174), (6.175), рівняння (6.179) можна перетворити до виду

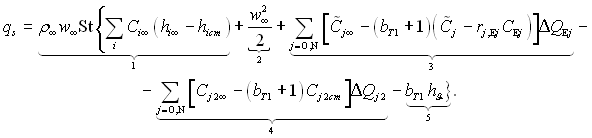(6.186)

У цьому виразі для простоти не розглядаються реакції, які ведуть до утворення двоокисів, тому що при високих температурах поверхні Ej2 дуже малі. Це рівняння отримане в припущенні, що Le = Sc = Pr = 1, дозволяє виділити різні фактори, що впливають на теплообмін при наявності хімічних реакцій в пограничному шарі.

Так, перший член представляє собою перенесення теплоти за рахунок теплопровідності; другий – дисипацію в пограничному шарі; третій – ураховує теплоту, яка виділяється при утворенні компонентів під час хімічних реакцій; четвертий – поглинання теплоти при дисипації компонентів; п’ятий – поглинання теплоти за рахунок випаровування поверхні (сублімацію).

Таким чином, зменшення швидкості утворення компонентів, збільшення швидкості дисоціації і возгонки приводять до значного зменшення тепловіддачі до поверхні.

Аналіз отриманого виразу для теплового потоку (6.186) показує, що якщо відомі граничні умови, то при прийнятих допущеннях можна розрахувати значення теплового потоку, не враховуючи при цьому явища, що відбуваються в пограничному шарі. Але варто мати на увазі, що величина q_S залежить в неявній формі від процесів, які відбуваються в пограничному шарі, через число St. Для визначення величини числа Стентора, що входить в рівняння (6.186), необхідно розв’язати інтегральне співвідношення енергії для конкретних граничних умов.

● Розрахунок конвективного теплообміну на хімічно реагуючій поверхні. При числах Le = 1 і незалежності переносних властивостей від складу суміші тепловий потік не залежить від того, де розташована зона хімічних реакцій.

Отже, можна вважати, що хімічні реакції протікають тільки безпосередньо біля поверхні тіла. У цьому випадку склад газової суміші в поперечному перерізі пограничного шару визначається тільки процесами конвекції і дифузії продуктів реакції і реагуючих речовин. Такий пограничний шар називається “замороженим”.

Таким чином, розрахунок теплообміну при наявності хімічних реакцій, вважаючи “замороженим” пограничний шар, принципово не повинен відрізнятися від аналогічних розрахунків теплообміну на половину проникливій поверхні. У цьому випадку справедливі і закони теплообміну (6.142), (6.162), які враховують вплив неізотермічності і поперечного потоку речовини.

Інтегральне рівняння енергії для випадку обтікання стисливим реагуючим газом неізотермічної поверхні має вид

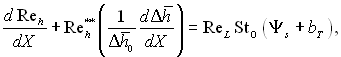(6.187)

де

Розв’язок цього лінійного диференціального рівняння має наступний вид

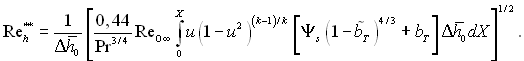(6.188)

Величина локального числа Стентора знаходиться з рівняння

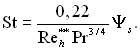(6.189)

Інтенсивність випарювання (вигорання) поверхні визначається з виразу

(6.190)

Параметр вдування b_T1, як було показано раніше, можна визначити розрахунком рівноважного складу за рівнянням, аналогічним (6.185).

Сумарний тепловий потік, який доходить до поверхні, розраховується за рівнянням (6.186).

Розглянутий у цьому параграфі метод розрахунку теплообміну при наявності хімічних реакцій можна застосовувати також і для розрахунку турбулентного пограничного шалу, якщо в рівняння (6.187) підставити відповідний вираз для закону теплообміну, справедливого для турбулентного пограничного шару.

У рівняннях (6.188), (6.190) температура поверхні теплообміну повинна бути заданою величиною. Але у багатьох випадках вона є шуканим параметром і визначається не тільки хімічними реакціями на поверхні тіла і інтенсивністю теплообміну з потоком газу, що набігає на неї, але і інтенсивністю відведення теплоти в тверде тіло.

В деяких випадках відведенням теплоти всередину тіла можна знехтувати (наприклад, при сублімації вуглецю) і тоді температура поверхні визначається з рівняння (6.186), вважаючи що q_S = 0.

В іншому граничному випадку можна вважати, що швидкість возгонки приймає усталене значення і сублімаційний матеріал прогрівається від певної початкової температури Т_п до температури поверхні стінки Т_ст, тобто

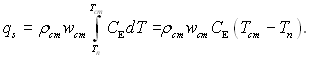(6.191)

З рівняння (6.186) з урахуванням (6.191) слідує

(6.192)

де

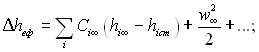(6.193)

С_Е – теплоємність матеріалу стінки. Звідси

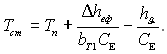(6.194)

Строго кажучи, рівняння (6.193) і (6.194) розв’язуються методом послідовних наближень чи графічним методом. У цьому випадку рівняння (6.192) зручно записати так:

(6.195)

Ліва і права частини рівняння залежать від температури поверхні; перетин цих залежностей в графічному виконанні і дає шукане значення температури поверхні.

6.3. Вимушена конвекція при турбулентному русі рідини

6.3.1. Виникнення турбулентної течії

О.Рейнольдс, вивчаючи рух води в круглих циліндричних трубах, виявив наявність двох режимів течії рідини: ламінарного і турбулентного.

При ламінарному (шаруватому) режимі течії частинки рідини рухаються за повністю визначеними траєкторіями. При цьому, як показав аналіз результатів рішень, наведених вище, загальні закономірності ламінарної течії рідини добре описуються рівнянням Нав’є–Стокса.

Але при певних умовах зі збільшенням швидкості ламінарний рух губить свою стійкість, при цьому початкові подразнення, розвиваючись, приводять до нової форми руху, яка представляє собою хаотичний рух мас рідини. Процес виникнення і розвитку такого режиму руху носить випадковий характер і вимагає для свого вивчення статистичного підходу. Ця широко розповсюджена в природі форма руху називається турбулентною течією.

Рейнольдс показав, що перехід від одного режиму течії до другого відбувається при певному значенні числа Re. Так, на підставі чисельних дослідів було установлено, що течія рідини в круглих трубах завжди носить ламінарний характер, якщо Re ≤ 2200, де Re = w_cpd/ν; d – діаметр труби; w_cp – середня швидкість.

При цьому течія стійка по відношенню до любих подразнень. Назване цифрове значення числа Re називається критичним числом Рейнольдса (Re_кр) і визначає нижню границю ламінарної течії. Дослідним шляхом не вдалося отримати певне значення числа Re для верхньої границі, тому що ця границя при створенні спеціальних штучних умов (плавного входу, гладкої поверхні та ін.) багаторазово змінювалися аж до Re = 5·10⁴.

У перехідній області Re_кр< Re < 5·10⁴ течія нестійка і любе, навіть дуже мале, подразнення приводить до виникнення турбулентного режиму руху.

Ретельне дослідження руху рідини в трубах при Re ~ Re_кр показало, що в одному і тому ж перерізі труби відбувається чергування ламінарного і турбулентного режимів течії. Це явище носить назву “переміжності”. Причина “переміжності” криється в тому, що турбулентність зароджується в дискретних областях потоку в вигляді пробок, протяжність яких залежить від числа Re. Для кількісної міри “переміжності” служить коефіцієнт переміжності γ, який представляє собою частку часу існування турбулентної течії в даному перерізі труби.

На рис.6.25 наведені діаграми пульсації повздовжньої складової швидкості в перехідній області (Re_x = 2·10⁶, ступінь турбулентності зовнішнього потоку ε = 0,0025%) для точок, що знаходяться всередині пограничного шару. На діаграмах чітко розрізняються чергуючи області турбулентного і ламінарного руху рідини. Перехідні явища в пограничному шарі крім числа Re і ступеня турбулентності зовнішнього потоку залежать ще і від таких факторів, як зміна тиску на зовнішній межі пограничного шару, стану поверхні, поперечного потоку речовини, стисливості і неізотермічності.

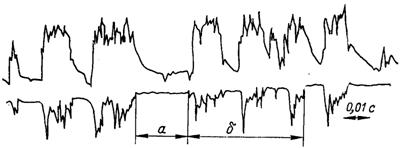
Рис.6.25. Діаграма пульсацій повздовжньої складової швидкості в перехідній області течії в пограничному шарі на пластині: а – ламінарна течія; б – турбулентна течія; у = 0,4 мм – верхня крива; у = 2,1 мм – нижня крива

На пластині з гострою передньою кромкою, яка обдувається потоком повітря перехід ламінарного режиму течії до турбулентного в пограничному шарі відбувається на відстані х від передньої кромки і визначається з формули:

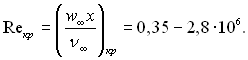(6.196)

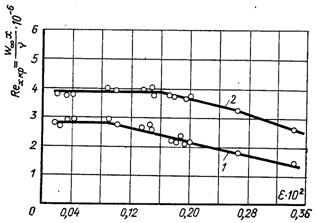
Рис.6.26. Вплив ступеня турбулізації ε на Re_кр для плоскої пластини, що обтікає в повздовжньому напрямку (дані Шубауера і Скремстеда): 1 – ламінарна течія; 2 – турбулентна течія

Значення Re_кр залежить від початкового ступеня турбулентності набігаючого потоку. На рис.6.26 наводяться дані, з яких слідує, що при зменшенні ступеня турбулентності значення Re_кр спочатку збільшується, а далі, досягнувши Re_кр = 2,8·10⁶ при ε = 0,0008, зберігається постійним при подальшому зменшенні ступеня турбулентності. Це значить, що для критичного числа Рейнольдса на поздовжньо обтікаючій пластині існує і верхня границя.

На величину Re_кр також суттєво впливає і зміна тиску на зовнішній межі пограничного шару. Так при конфузорній течії критичне значення числа Re більше, а при дифузорному – значно менше, ніж при обтіканні пластини. Виходячи з цього, для конфузорної ділянки пограничного шару, де потік на зовнішній межі пограничного шару прискорюється, перехід до турбулентного режиму течії затягується, зміщуючись вниз за потоком, а в дифузорному, навпаки, виникає раніше.

6.3.2. Рівняння турбулентного пограничного шару

Диференціальні рівняння руху, нерозривності потоку, енергії і дифузії для осередненого руху в турбулентному пограничному шарі стисливої рідини отримуємо шляхом порівняльної оцінки величини членів, які входять в диференціальні рівняння системи (6.68)...(6.73). Зберігши в названих рівняннях найбільші члени одного і того ж порядку, отримаємо наступну систему рівнянь усталеного плоского стисливого турбулентного пограничного шару:

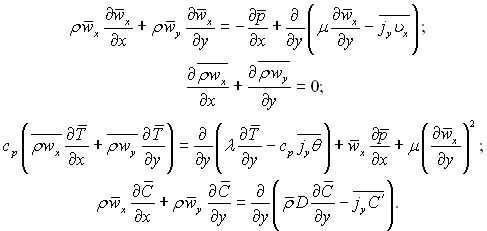(6.197)

Інтегральні рівняння руху, енергії і дифузії турбулентного пограничного шару виводяться з рівнянь (6.197) так само, як і у випадку ламінарного шару і мають той же вид (ці рівняння також можна отримати, розглядаючи баланс кількості руху, енергії і речовини для елементарного об’єму рідини):

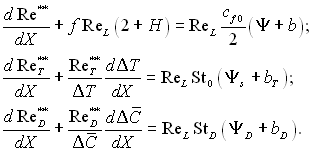(6.198)

Але, як буде показано нижче, на відміну від ламінарного пограничного шару закони опору, теплообміну і масообміну не можуть бути отримані шляхом вирішення системи диференціальних рівнянь (6.197), тому що ця система незамкнена.

6.3.3. Турбулентна дотична напруга, тепловий і дифузійний потоки

Співставляючи диференціальні рівняння ламінарного пограничного шару з отриманими для осереднених величин рівняннями турбулентного пограничного шару, неважко замітити, що в турбулентному пограничному шарі виникають додаткові турбулентні напруження тертя, тепловий і дифузійний потоки, які визначаються співвідношеннями

(6.199)

Тут j_y – пульсаційна складова витрат, яка визначається з рівняння

(6.200)

Використовуючи рівняння (6.200), співвідношення (6.199) можна переписати в наступному вигляді

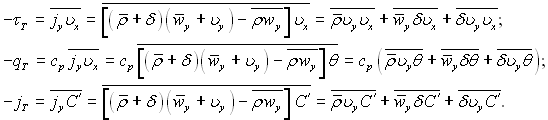(6.201)

У цьому рівнянні δ, θ і С′  визначаються зі співвідношень

Під час руху нестисливої рідини (δ = 0) співвідношення значно спрощуються і набувають вигляду

(6.202)

Якщо вважати, що пульсації густини пов’язані тільки з пульсаціями температурного поля, тобто ρ = ρ(Т), і не залежить від тиску, то

У цьому рівнянні β = 1/Т – коефіцієнт об’ємного розширення.

У цьому випадку вираз для турбулентного тертя, теплового потоку і дифузійного потоку (6.201) набувають наступного виду:

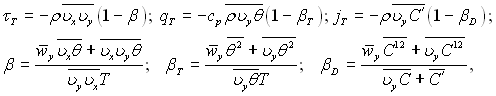(6.203)

де коефіцієнти β, β_Т, β_D враховують вплив флуктуації температури, концентрації і швидкості на величини τ_Т, q_T і j_T.

З рівнянь (6.203) виходить, що між потоками імпульсу, теплоти і маси в турбулентному пограничному шарі існує тісний зв’язок, який широко використовується під час розрахунків процесів тепло- і масообміну.