ПОДВІЙНОЇ КРИВИЗНИ
3.1 Загальні відомості про оболонки
3.1.3 Геометрія серединної поверхні оболонки
3.1.3 Геометрія серединної поверхні оболонки
Розглянемо ділянку довільної поверхні “а” оболонки (рис. 3.1.3). В точці “с” проведемо нормаль до неї. Довільна площина “в”, що включає цю нормаль, (тобто нормальна площина) перетинається з поверхнею “а” по плоскій кривій α, радіус головної кривизни (radius of the main curvature) якої в околі точки “с” позначимо R, а центр кривизни – O.
Величину k = 1/R називають кривизною кривої α в околі точки “с”.
Якщо повертати площину “в” навколо нормалі “n”, отримаємо на поверхні “а” ряд кривих, що проходять через точку “с”. Центр кривизни буде при цьому переміщуватись уздовж нормалі. Відмітимо два його положення: О1 і О2 – найбільш і найменш віддалені від поверхні “а”. Цим центрам відповідають максимальний і мінімальний (R1, R2) радіуси, які називають головними радіусами кривизни поверхні “а” в точці “с”.
Відповідно k1 = 1/R1 і k2 = 1/R2 називають головними кривизнами. Їм відповідають на поверхні “α,” лінії α1 і α2, що називаються лініями головних кривизн. В довільній точці поверхні лінії головних кривизн нормальні одна одній.
На будь-яку поверхню можна нанести ортогональну сітку, що складається із ліній головних кривизн (рис. 3.1.4, а).
Лінії головних кривизн характерні ще й тим, що уздовж них відсутнє кручення поверхні. Це означає, що коли взяли 2 елементи: елемент t, утворений двома парами ліній головних кривизн, і елемент t*, утворений будь-якими іншими ортогональними лініями, то, спроектувавши їх на нормальні плоскості, відповідно b і b*, побачимо (рис. 3.1.4, б), що другий з них закручений, а перший – ні.
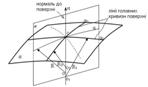
Рисунок 3.1.3 – Визначення ліній і радіусів головних кривизн поверхні
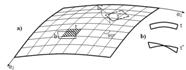
Рисунок 3.1.4 – Сітка головних кривизн поверхні
Величина
K = k1∙k2 =  |
(3.1.1) |
називається гаусовою кривизною. Важливою характеристикою поверхні є знак гаусової кривизни, який залежить від того, як розташовані центри головних кривизн відносно поверхні (рис. 3.1.5).
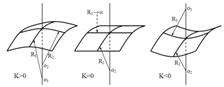
Рисунок 3.1.5 – Визначення знака гаусової кривизни поверхні
Гаусова кривизна серединної поверхні визначає загальну жорсткість оболонки, тобто її властивість зберігати початкову форму при дії зовнішніх сил. Найбільш жорсткими в цьому понятті є оболонки із серединною поверхнею, що мають додатну гаусову кривизну, скорочено їх називають оболонками додатної гаусової кривизни.
Менш жорсткі оболонки характеризуються нульовою гаусовою кривизною. Найменш жорсткі оболонки – з від’ємною гаусовою кривизною.
Серединні поверхні оболонок, що їх використовують в будівництві, можуть бути утворені різними способами. Найбільш важливі випадки:
- оболонки обертання (рис. 3.1.6), утворені обертанням плоскої кривої навколо прямої лінії. Для таких поверхонь лінії головних кривизн є меридіанами і паралелями;
- Оболонки перенесення (рис. 3.1.7), утворені переміщенням плоскої кривої f, що лежить у вертикальній площині b, по двох напрямних кривих S, що лежать також у вертикальних плоскостях, перпендикулярних до площини b.
- лінійчасті оболонки (рис. 3.1.8) утворені переміщенням прямої лінії по двох прямих (але не паралельних) або кривих напрямних.
Деколи одну і ту ж саму поверхню можна утворювати різними способами. Так, циліндрична поверхня може вважатись поверхнею обертання, лінійчатою поверхнею і поверхнею перенесення; гіперболоїд обертання можна утворити лінійчатою поверхнею.
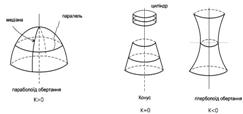
Рисунок 3.1.6 – Оболонки обертання
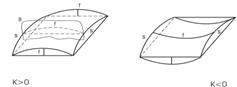
Рисунок 3.1.7 – Оболонки перенесення
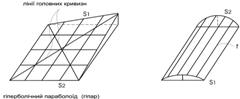
Рисунок 3.1.8 – Лінійчаті оболонки


