ПОДВІЙНОЇ КРИВИЗНИ
3.1 Загальні відомості про оболонки
3.1.4 Внутрішні зусилля, деформації, переміщення в оболонках
3.1.4 Внутрішні зусилля, деформації, переміщення в оболонках
Коли відношення товщини оболонки δ до найменшого із головних радіусів кривизни не перевищує 1/20, то така оболонка вважається тонкою. (В реальних конструкціях це відношення може сягати 1/200 – 1/300).
Внутрішні зусилля в оболонці діляться на 2 групи:
а) зусилля мембранного типу (рис. 3.1.9, а): нормальні N1, N2 і зсувні S12, S21; такі зусилля можуть виникати в плоскому диску чи в тонкій мембрані;
б) зусилля моментного типу (рис. 3.1.9, б): згинальні моменти М1, М2, крутні моменти М12, М21, поперечні сили Q1, Q2; такі зусилля можуть виникати в тонких пластинах.
Для тонких оболонок можна з достатньою точністю прийняти, що
| S12 = S21M = S; M12 = M21 = Mk. | (3.1.2) |
Під дією зовнішнього навантаження оболонка деформується, а точки її серединної площини переміщуються. Складова переміщень вздовж ОХ позначається u (рис. 3.1.9, в), в напрямі осі OY – v, в напрямі осі OZ – w (це прогин оболонки).
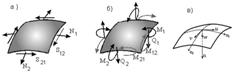
Рисунок 3.1.9 – Види зусиль та переміщень в оболонках
В випадку просторової задачі теорії пружності відносні подовження або лінійні деформації вздовж осей координат пов’язані з функціями лінійних переміщень диференціальними співвідношеннями
| (3.1.3) |
Відносні зсуви, або кутові деформації, пов’язані з переміщеннями співвідношеннями
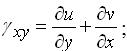 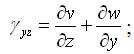 |
(3.1.4) |
Виходячи з гіпотези прямих недеформованих нормалей вважається, що елементи матеріалу, які розташовані вздовж нормалі, не зазнають деформацій зсуву в площинах XOZ, YOZ, тобто
| (3.1.5) |
а розмір елемента в напрямі осі OZ не змінюється, отже відповідна лінійна деформація нульова
| (3.1.6) |
Останнє співвідношення виконується лише тоді, коли прогини оболонки є функціями тільки двох координат x і y: w = w(x, y). Отже, у всіх точках, які розташовані на вертикальній прямій, прогини однакові, постійні вздовж осі OZ.
Таким чином, в оболонці виникають лінійні деформації εx , εy; кутові λxy; деформації викривлення æ1, æ2 та кручення χ.
Між зусиллями та деформаціями існує відповідність:
N → εy; M → æ2;
S → λxy; Mk → χ.
Зусиллям Q1, Q2 не відповідають ніякі деформації в силу гіпотези 1, де висловлюється думка, що в поперечних перерізах оболонки відсутні деформації зсуву.
В випадку просторової задачі теорії пружності згідно із законом Гука лінійні деформації вдовж осей ОХ, ОY в пружному тілі визначаються за формулами:
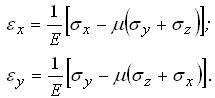 |
(3.1.7) |
За гіпотезою про відсутність тиску між шарами матеріалу оболонки ![]() слід знехтувати (
слід знехтувати (![]() = 0), а лінійні деформації будуть такими, як при плоскому напруженому стані:
= 0), а лінійні деформації будуть такими, як при плоскому напруженому стані:
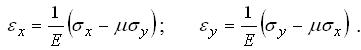 |
(3.1.8) |
Нормальні напруження можна виразити через лінійні деформації:
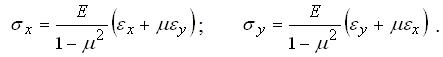 |
(3.1.9) |
Дотичні напруження згідно із законом Гука при зсуві:
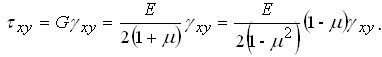 |
(3.1.10) |
Враховуючи [22, 23], одержимо такі формули для основних розрахункових напружень в оболонці:
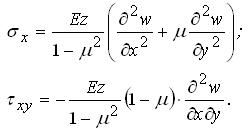 |
(3.1.11) |
Напруження (3.1.7-3.1.11) характеризують міцність оболонки. Вони є функціями лише двох координат: σx = σx(x,y); σy=σy(x,y); τxy(x,y). Тому задача про згинання оболонок в математичному аспекті буде двовимірною, а у фізичному – просторовою (тривимірною).
З рівнянь рівноваги тривимірного тіла можна визначити також напруження σz, τxz, τyz які називаються додатковими. Порівняно з основними, ці напруження невеликі і неістотно впливають на міцність оболонки.
Таким чином, в теорії оболонок розглядаються 8 зусиль, 6 деформацій і 3 переміщення. Кожна з цих величин є функцією двох координат (в загальному випадку криволінійних).
Зовнішнє навантаження, що діє на оболонку, задається у вигляді проекцій на координатні осі X, Y, Z, і самі проекції позначаються через ![]()
Коли в якійсь області оболонки діють лише мембранні зусилля, тоді такий напружений стан має назву безмоментний. При цьому напруження в поперечних перерізах розподіляються рівномірно по товщині і несуча спроможність матеріалу використовується найповніше.
Саме тому оболонки дають можливість перекривати в десятки разів більші прогони, ніж з використанням пластин тієї ж товщини і стають вельми економічними конструкціями. При проектуванні оболонок завжди прагнуть до того, щоб зусилля моментної групи були якомога меншими за величиною і діяли в обмежених областях.


