ПОДВІЙНОЇ КРИВИЗНИ
3.2 Основи теорії похилих оболонок подвійної кривизни
3.2.1 Основні ознаки похилих оболонок
3.2.1 Основні ознаки похилих оболонок
Оболонку вважають похилою, коли її геометричні розміри такі, що виконується умова:
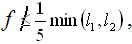 , , |
(3.2.1) |
тобто, якщо стріла підняття оболонки в центрі f не перебільшує 1/5 довжини меншої сторони оболонки в плані (рис. 3.2.1) або
| f1 |
(3.2.2) |
де f1, f2 – стріли підняття сторін контуру,
l1 , l2 – розміри оболонки в плані.
Очевидно, що похила оболонка подвійної кривизни, зображена на рис. 3.2.1, характеризується додатною гаусовою кривизною і їй властива велика жорсткість. Такі оболонки на наш час достатньо широко використовуються для влаштування як залізобетонних, так і металевих великопрогонових покрить. Оболонки подвійної кривизни, що характеризуються додатною гаусовою кривизною, потребують найменшої кількості опорних закріплень, завдяки чому складаються виключно сприятливі умови для експлуатації приміщень промислового та цивільного призначення.
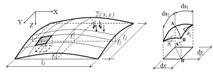
Рисунок 3.2.1 – Геометрія похилої оболонки
Ефективною тактикою розв’язування задачі про напружено- деформований стан оболонок є теорія похилих оболонок, яка була напрацьована в другій половині 40-х років В. З. Власовим [10]. Вона лежить в основі більшості методів розрахунку згаданих вище конструкцій.


