ПОДВІЙНОЇ КРИВИЗНИ
3.2 Основи теорії похилих оболонок подвійної кривизни
3.2.3 Диференціальні рівняння рівноваги елемента похилої оболонки
3.2.3 Диференціальні рівняння рівноваги елемента похилої оболонки
Для елемента оболонки можна записати 6 умов рівноваги:
| 1) ∑X=0, 4) ∑Mx=0, 2) ∑Y=0, 5) ∑My=0, 3) ∑Z=0, 6) ∑Mz=0. |
(3.2.5) |
Якщо взяти до уваги (3.1.2), то рівняння 6 перетворюється в тотожність. Залишається 5 рівнянь.
При запису 1-го і 2-го рівнянь можна знехтувати проекціями поперечних сил на осі Х і Y порівняно з проекціями нормальних і зсувних сил на ці ж осі (наприклад, Q1 sinθ1<<N1 cosθ1, дійсно sinθ1<<cosθ1), а крім того, зазвичай Q1 < N1. Тоді отримані рівняння не будуть відрізнятись від відповідних рівнянь елемента плоского диска, які при відсутності компонент навантаження ![]() , а також сил інерції мають вигляд [23]:
, а також сил інерції мають вигляд [23]:
| (3.2.6) |
Внутрішні зусилля мембранного типу записуються через напруження так:
| N1=σx·δ, N2=σy·δ, S=τxy·δ, | (3.2.7) |
де δ - товщина оболонки.
Помноживши (3.2.6) на δ і враховуючи (3.2.7) отримаємо для похилої оболонки дві перші умови рівноваги в такому вигляді:
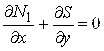 ; ; |
(3.2.8) |
Для похилої оболонки четверта та п’ята умови рівноваги:
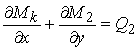 . . |
(3.2.9) |
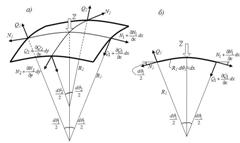
Рисунок 3.2.2 – Внутрішні зусилля серединної поверхні оболонки, що дають ненульові проекції на вісь Z
На рис. 3.2.2 наведено елемент серединної поверхні похилої оболонки з внутрішніми зусиллями, що дають ненульові проекції на вісь Z.
Сума проекції сил на вісь Z дає:
| (3.2.10) |
Розділивши (3.2.10) на dx×dy і, враховуючи що:
 , ,  ; ; |
(3.2.11) |
отримаємо
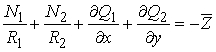 . . |
(3.2.12) |
При R1 = R2 → ∞, тобто, коли похила оболонка вироджується в пластинку, це рівняння пов’язує в пластинці похідні поперечних сил і зовнішнє навантаження.
Таким чином, для похилої оболонки система рівнянь рівноваги, записана через внутрішні зусилля, має вигляд:
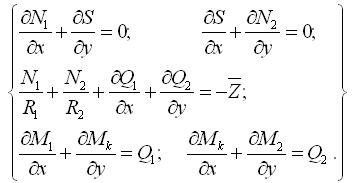 |
(3.2.13) |
Оскільки невідомих зусиль більше, ніж рівнянь рівноваги, задача розрахунку оболонки є статично невизначеною і для її розв’язку необхідно додати геометричні та фізичні рівняння.


