Відомо, що при σ_z=0 закон Гука можна подати в вигляді залежностей:

.

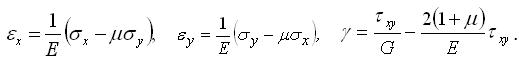Враховуючи це, а також (3.2.7),  можна записати:

.

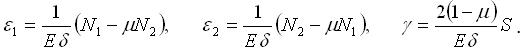(3.2.17)

Залежність між внутрішніми зусиллями моментного типу і переміщеннями w, враховуючи пологість оболонок, приймається такою, як і в теорії згину пластин [22]:

;     ;

;

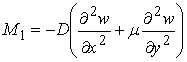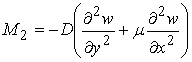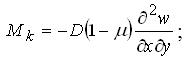(3.2.18)

.

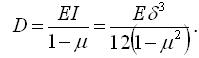(3.2.19)

Із 4-го та 5-го рівнянь рівноваги (3.2.13) і рівнянь (3.2.18) отримаємо вирази для поперечних сил, також відомі із теорії згину пластин:

,

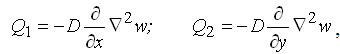(3.2.20)

де 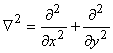– бігармонічний оператор Лапласа .

(3.2.21)

Таким чином отримаємо: 5 рівнянь рівноваги (3.2.13), 6 геометричних рівнянь (3.2.14) – (3.2.16) і 6 фізичних (3.2.17), (3.2.18) – всього 17 рівнянь для визначення 17 невідомих (8 зусиль, 6 деформацій, 3 переміщення).