П’ять рівнянь рівноваги (3.2.13), одне рівняння сумісності деформацій (3.2.23) та шість фізичних залежностей (3.2.17), (3.2.18) пов’язують 8 невідомих внутрішніх зусиль:  N₁, N₂, S, M₁, M₂, M_к, Q₁, Q₂; 3 деформації ε₁, ε₂, γ  і одне переміщення w. Для зручності розв’язання цієї системи, що складається із 12 диференціальних і алгебраїчних рівнянь, вводиться функція напружень φ(x,y). Подібна функція φ₁(x,y) використовується в [22] та задається виразами:

,      ,

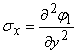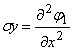(3.2.24)

Відомо, що при зведенні напружень σ_x, σ_y, τ_xy в вигляді (3.2.24) тотожно задовольняються рівняння рівноваги (3.2.6).

Із (3.2.24) випливає, що φ=φ₁·δ. Природно, що мембранні зусилля подаються у вигляді:

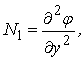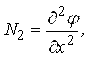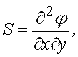(3.2.25)

і це приводить до тотожного задоволення двох перших рівнянь (3.2.13).

В формулах (3.2.17) за допомогою залежностей (3.2.25) можна виразити зусилля N₁,  N₂, S через функцію напружень φ:  

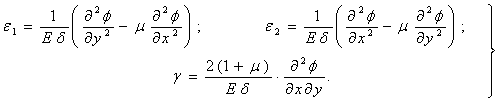(3.2.26)

Підставимо в третє із рівнянь рівноваги (3.2.13) вирази для поперечних сил (3.2.20) і для мембранних зусиль (3.2.25):

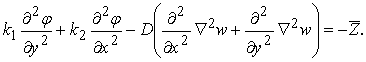
Використаємо позначення (3.2.21) і (3.2.22) і отримаємо диференціальне рівняння:

.

(3.2.27)

Якщо підставити вираз для деформації (3.2.26) в рівняння сумісності деформацій (3.2.23), то воно набуде вигляду:

.

(3.2.28)

Позначимо  і отримаємо систему двох розрахункових рівнянь теорії похилих оболонок в вигляді:

(3.2.29, а)

або

(3.2.29, б)

Рівняння (3.2.29) є рівняннями змішаного методу. Дійсно, тут одна невідома функція (φ) – силова, інша (w) – геометрична.

Перше рівняння виведене на основі умови рівноваги, друге – на основі умови сумісності деформацій. Нарешті, оператори, розташовані симетрично відносно головної діагоналі (3.2.29, а), відрізняються лише знаком, що характерно для системи рівнянь змішаного типу.

Природно, що при розв’язанні конкретних задач до системи розрахункових рівнянь (3.2.29) потрібно приєднати умови на контурі.

Слід зазначити, що при:

де   R₁, R₂ – радіуси кривизн;    k₁, k₂ – кривизни.

Тобто, коли серединна поверхня оболонки вироджується в площину, система рівнянь (3.2.29) розкладається на 2 самостійні диференціальні рівняння в частинних похідних. Перше із цих рівнянь, як видно із (3.2.29,б), є бігармонічним рівнянням плоскої задачі, друге – основним рівнянням згину пластин [22, 23].

Перше із них побудоване для розв’язання задачі в напруженнях, а друге – для розв’язання в переміщеннях.

Функції w і φ є розрахунковими. Тобто, через них можна виразити мембранні зусилля (3.2.25), згинальні та крутні моменти (3.2.18), поперечні сили (3.2.20), а також підставивши (3.2.26) в (3.2.14), можна отримати вирази для переміщень u і v:

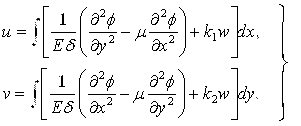(3.2.31)