ПОДВІЙНОЇ КРИВИЗНИ
3.2 Основи теорії похилих оболонок подвійної кривизни
3.2.8 Умови на контурі похилої оболонки
3.2.8 Умови на контурі похилої оболонки
Як відомо, при розв’язуванні конкретних задач з розрахунку похилих оболонок до системи диференціальних розрахункових рівнянь (3.2.29) необхідно додати умови на контурі.
Згідно з першою гіпотезою теорії тонких оболонок лінійний елемент краю оболонки, нормальний до серединної поверхні, в процесі деформації має розглядатись як абсолютно жорсткий. На рис. 3.2.4 такі елементи позначені АВ і A'B'. Положення такого елемента після деформації визначають 4 величини: три компоненти переміщень середини елемента (С та С1) – u, v, w і кут повертання елемента в площині, нормальній до серединної поверхні і до контурного перерізу (ψ1 чи ψ2, залежно від того, як направлена нормаль до контурного перерізу).
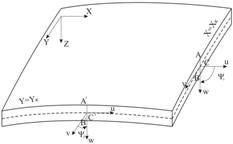
Рисунок 3.2.4 – Криволінійний елемент оболонки
Згідно з цим умови жорсткого закріплення, наприклад сторони контуру у = ук прямокутної оболонки, записуються так :
| u = 0, v = 0, w = 0, ψ2 = |
(3.2.32) |
Тепер розглянемо випадок, коли на вільній стороні контуру прямокутної похилої оболонки, наприклад х = хк, відсутні внутрішні зусилля. Умовою того, що ця сторона контуру вільна, має бути рівність нулю п’яти внутрішніх зусиль: N1, S, M1, Mк (МК=М12=М21), Q1, (рис. 3.1.9). Але диференціальні рівняння задачі такі (3.2.29), що на кожній стороні контуру можливе задоволення лише чотирьох умов. В силу цього, на контурі крутні моменти замінюються статично еквівалентними поперечними силами, точно так, як це робиться в теорії згину пластин.
Іншими словами, в теорії похилих оболонок при запису умов на контурі зусилля Mк, Q1 а також Q2, Mк замінюються статично еквівалентними поперечними силами Q*1, Q*2 [23, 28]:
| (3.2.33) |
Таким чином, граничні умови на вільній від закріплень стороні контуру х = хк/ прямокутної похилої оболонки записуються у вигляді:
| N1 = 0, S = 0, Mк = 0, Q*1 = 0. | (3.2.34) |
Із (3.2.32 ) і (3.2.34) видно, що умови на жорстко закріпленій стороні контуру записуються в переміщеннях, а на вільній – в зусиллях. Умови на контурі можуть бути і змішаного типу, тобто можливе задання частини умов в зусиллях, частини – в переміщеннях.
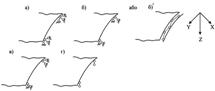
Рисунок 3.2.5 – Закріплення контуру оболонки
Так на рис. 3.2.5, а показано шарнірно нерухоме закріплення краю х = хк.
Граничні умови тут такі:
| u=0, v=0, w=0, M1=0. | (3.2.35) |
На рис. 3.2.5, б показано шарнірно рухоме закріплення з рухомістю в напрямку осі Х. Граничні умови:
| v=0, w=0, N1=0, M1=0. | (3.2.36) |
(В теорії оболонок таке закріплення прийнято називати „шарнірним” і зображується воно так, як показано на рис. 3.2.5, б).
Рис. 3.2.5, в – шарнірно рухоме закріплення з рухомістю в напрямку осі Y.
Граничні умови:
| u=0, w=0, S=0, M1=0. | (3.2.37) |
Рис. 3.2.5, г – шарнірне закріплення в напрямку осей х, у або радіальне обпирання. Граничні умови:
| S=0, w=0, N1=0, M1=0. | (3.2.38) |
Всього можна зобразити 8 видів шарнірних закріплень контуру зв’язками, а загальна кількість варіантів закріплення контуру, що не деформується, – 16. Та цими варіантами умов на контурі не вичерпується вся їх множина. Можливе накладання на контур різного роду пружних зв’язків, а також прикріплення контуру чи його частини до елементів конструкцій арками, фермами і т.д. В цьому випадку умови на контурі описують умови контакту краю оболонки з елементом, до якого прикріплений цей край.


