ПОДВІЙНОЇ КРИВИЗНИ
3.3 Розрахунок похилих оболонок подвійної кривизни з шарнірним обпиранням по всьому контуру
3.3.1 Розв'язування в подвійних тригонометричних рядах. Випадок довільного навантаження
3.3.1 Розв'язування в подвійних тригонометричних рядах. Випадок довільного навантаження
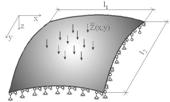
Рисунок 3.3.1 – Похила оболонка з шарнірним закріпленням по контуру
Одержати інтеграл системи диференціальних рівнянь (3.2.29, а) в замкнутому вигляді можна лише в не багатьох випадках.
Найбільш поширені різноманітні наближені методи розрахунку, до яких належить метод подвійних тригонометричних рядів – метод Нав’є.
Нехай похила оболонка додатної гаусової кривизни (рис. 3.3.1) шарнірно закріплена по всьому контуру, як показано на рис. 3.2.5, б1.
Граничні умови згідно з (3.2.36)
| при х=0, і x=l1: w=0, N1=0, M1=0, v=0; | (3.3.1) |
| при у=0, у=l2: v=0, w=0, N2=0, M2=0. |
Невідомі функції системи диференціальних рівнянь (3.2.29) подамо в вигляді нескінченних подвійних тригонометричних рядів
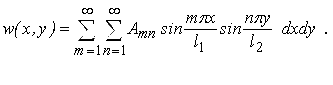 |
(3.3.2) |
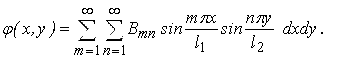 |
(3.3.3) |
де ![]() – невідомі постійні коефіцієнти, які потрібно визначити;
– невідомі постійні коефіцієнти, які потрібно визначити;
m,n – додатні цілі числа натурального ряду 1, 2, 3...
Цей метод розв’язування розрахункових рівнянь теорії похилих оболонок був запропонований В. В. Власовим [10].
Величину зовнішнього навантаження ![]() , що стоїть в правій частині другого рівняння (3.2.29), теж розкладемо в подвійний тригонометричний ряд на прямокутній області 0≤x≤l1, 0≤x≤l2 тобто:
, що стоїть в правій частині другого рівняння (3.2.29), теж розкладемо в подвійний тригонометричний ряд на прямокутній області 0≤x≤l1, 0≤x≤l2 тобто:
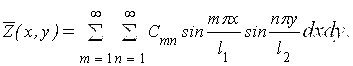 |
(3.3.4) |
Коефіцієнт Сmn – відома величина, що визначається згідно з теорією рядів Фур’є:
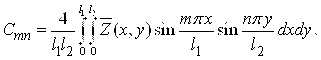 |
(3.3.5) |
Якщо функції (3.3.2), (3.3.3) є розв’язком задачі, вони мають задовольняти розрахункові диференціальні рівняння та граничні умови. При шарнірному обпиранні оболонки на її контурі прогини відсутні.
Відсутні також і згинальні моменти, тобто другі похідні функції прогину в напрямі, перпендикулярному до краю оболонки.
Другі похідні функції прогину мають вигляд
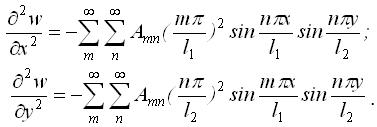
Звідки робимо висновок, що граничні умови виконуються, оскільки при х=0 та при х=l1 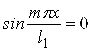 , а при у=0, у=l2
, а при у=0, у=l2 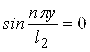 .
.
Якщо розгорнути граничні умови (3.3.1) за допомогою виразів (3.2.25), (3.2.18), (3.2.31), то побачимо, що для х=0, і для х=l1
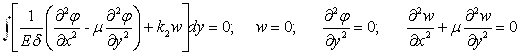 . . |
(3.3.6) |
В (3.3.6) входять похідні за х лише парних порядків, а оскільки при х=0, х=l1, величина 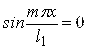 і будь-яка їх парна похідна перетворюється в нуль, то граничні умови задовольняються. Те ж можна показати і для країв у=0, у=l2.
і будь-яка їх парна похідна перетворюється в нуль, то граничні умови задовольняються. Те ж можна показати і для країв у=0, у=l2.
Для визначення коефіцієнтів Amn i Bmn підставляємо ряди (3.3.2), (3.3.3), (3.3.4) в систему (3.2.29, б):
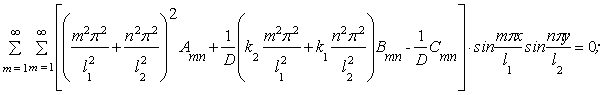 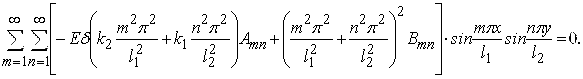 |
(3.3.7) |
Відомо, що якщо сума ряду, складеного за ортогональними функціями, дорівнює нулю, то має дорівнювати нулю будь-який коефіцієнт цього ряду. Оскільки функції ![]() ортогональні в проміжку 0≤x≤l1, а
ортогональні в проміжку 0≤x≤l1, а ![]() в проміжку 0≤x≤l2, то потрібно прирівняти до нуля коефіцієнти рядів (3.3.7), тобто вирази в квадратних дужках. В результаті отримуємо систему алгебраїчних рівнянь
в проміжку 0≤x≤l2, то потрібно прирівняти до нуля коефіцієнти рядів (3.3.7), тобто вирази в квадратних дужках. В результаті отримуємо систему алгебраїчних рівнянь
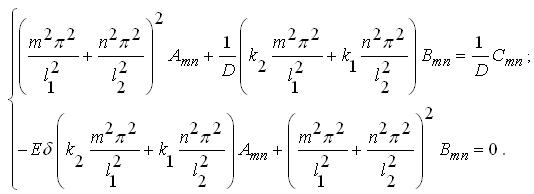 |
(3.3.8) |
Коренями цієї системи будуть вирази
 |
(3.3.9) |
Для спрощення формул введемо позначення 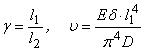 . Тоді
. Тоді
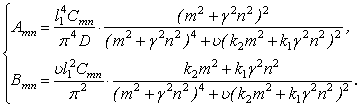 |
(3.3.10) |
Підставивши (3.3.2), (3.3.3) в (3.2.18), (3.2.20) і (3.2.25) можна отримати залежності для розрахунку
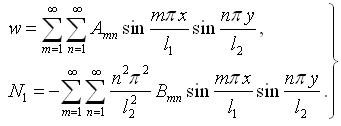 |
(3.3.11) |
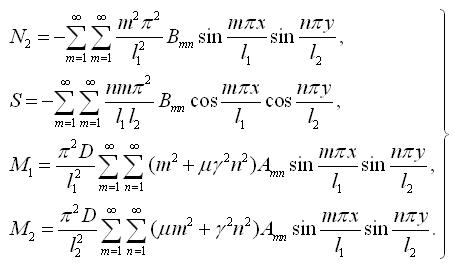 |
(3.3.11) |
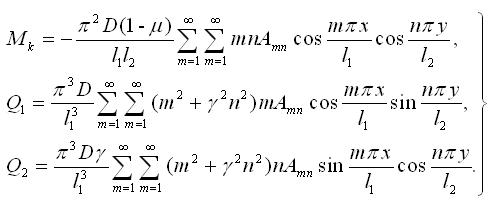 |
(3.3.13) |


