ПОДВІЙНОЇ КРИВИЗНИ
3.3.2 Розв'язування в подвійних тригонометричних рядах. Випадок рівномірно розподіленого навантаження
При 
=q=const вираз (3.3.5), який використовується при розрахунку як оболонок, так і пластин, набуває вигляду
 |
(3.3.14) |
Підстановка (3.3.12) в (3.3.11) дає
 , |
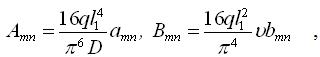(3.3.15) |
де
 |
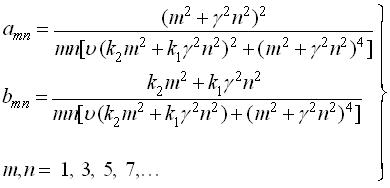(3.3.16) |
При підстановці (3.3.15) в (3.3.11, 3.3.12, 3.3.13) отримуємо розрахункові формули
 |
(3.3.17) |
Швидкість збіжності рядів (3.3.17) визначається структурою їх коефіцієнтів. Кожний з них являє собою дріб, чисельник і знаменник якого є багаточленами відносно індексів m і n. Чим більший степінь знаменника порівняно зі степенем чисельника, тим швидше збігається ряд.
Взагалі, ряди для мембранних зусиль мають більшу збіжність, ніж для моментних. В цьому можна впевнитись, порівнявши форми епюр тих і інших зусиль (рис. 3.3.2). В мембранних зусиллях вона більш плавна.
Декілька слів про фізичне тлумачення розкладання функцій в тригонометричний ряд Фур’є. Тригонометричні ряди Фур’є використовуються в теорії та практиці порівняно з іншими рядами Фур’є так часто, що зазвичай їх називають “просто” рядами Фур’є. Якщо функції w i φ – неперервні на сегменті [-p,p], то всі інтеграли [11] мають зміст і, таким чином, можна говорити про ряд Фур’є цієї функції і про його збіжність. Збіжність ряду Фур’є забезпечує умова Діріхле [11].
Якщо як незалежну змінну розглядати час, то функціональна залежність буде описувати деякий процес, що протікає в часі. Нехай цей процес зводиться до механічного руху системи, тобто до її просторових переміщень.
остає питання про подання руху на деякому відрізку шляху у вигляді комбінацій тих чи інших наперед заданих рухів. Цьому питанню руху буде відповідати розкладання функції, що описує цей рух, в функціональний ряд за заданими функціями.
Як окремий випадок, можна поставити питання про подання достатньо довільного руху на даному відрізку часу [-p,p] у вигляді одночасного здійснення деякого стаціонарного зміщення а також гармо- нічних коливань з періодами 
.
Оскільки довільне коливання такого вигляду можна записати виразом
 , |
(3.3.18) |
йому відповідатиме пара членів тригонометричного ряду
 , |
(3.3.19) |
де 
; 
Таким чином, пара сусідніх членів (3.4.36) тригонометричного ряду відповідає деякій гармонічній складовій (3.4.35) загального руху системи з періодом 2p/n і амплітудою An. Ця гармонічна складова зазвичай має назву n-ї гармоніки руху.
