ПОДВІЙНОЇ КРИВИЗНИ
3.4 Розрахунок похилих оболонок подвійної кривизни з більш
складними умовами на контурі
3.4.1 Оболонка з шарнірним обпиранням двох протилежних сторін контуру. Розв'язання в одинарних тригонометричних рядах
3.4.1 Оболонка з шарнірним обпиранням двох протилежних сторін контуру. Розв'язання в одинарних тригонометричних рядах
Оболонка на рис. 3.4.1 закріплена шарнірно-рухомо по краях х=0, х=l1, а по двох інших краях закріплення довільне; наприклад, один край може бути жорстко закріплений, інший – вільний.
Розв’язок системи (3.2.29) шукаємо в формі рядів:
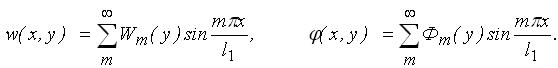 |
(3.4.1) |
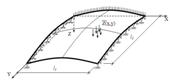
Рисунок 3.4.1 – Оболонка з різним обпиранням сторін
Навантаження подано теж у вигляді ряду:
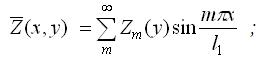 |
(3.4.2) |
де коефіцієнти знаходимо згідно з теорією рядів Фур’є:
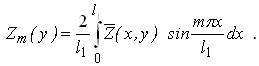 . . |
(3.4.3) |
Розв’язок (3.4.1) задовольняє умови шарнірного опирання по краях х=0, х=l1.
Підстановка (3.4.1) і (3.4.2) в систему (3.2.29, б) і прирівнювання до нуля коефіцієнтів за аналогією, як це було зроблено в 3.3.1, приводить до системи диференціальних рівнянь в звичайних похідних за змінною y:
 |
(3.4.4) |
Тут позначено: am = |
(3.4.5) |
Загальний розв’язок однорідної системи рівнянь, що відповідає (3.4.4) шукається у вигляді:
| (3.4.6) |
де Sm – постійна величина, поки що невідома;
Am, Bm - довільні постійні.
Підстановка (3.4.6) в (3.4.4) дає систему характеристичних рівнянь (алгебраїчних):
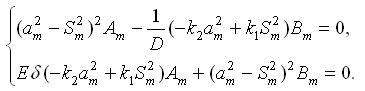 |
(3.4.7) |
Оскільки система (4.7) однорідна відносно Am , Bm, то ці величини будуть ненульовими лише тоді, коли визначник системи дорівнюватиме нулю:
 =0. =0. |
(3.4.8) |
З (3.4.8) отримуємо характеристичне рівняння:
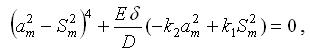 , , |
(3.4.9) |
що має 8 комплексних коренів такого вигляду:
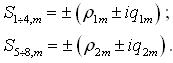 |
(3.4.10) |
(При m = 1 величини ![]() можна знайти із виразів (3.4.18) і (3.4.17)).
можна знайти із виразів (3.4.18) і (3.4.17)).
Із (3.4.7) можна знайти відношення 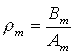 , їх має бути 8, як і Sm.
, їх має бути 8, як і Sm.
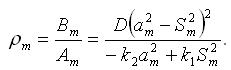 |
(3.4.11) |
В результаті, з урахуванням (3.4.6):
  |
(3.4.12) |
Ці розв’язки подаються в більш зручному вигляді за допомогою відомої залежності:
а саме:
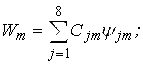 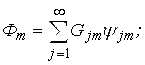 |
(3.4.13) |
де![]()
![]()
![]()
![]()
![]()
![]() (3.4.14)
(3.4.14)
![]()
![]()
Постійні ![]() пов’язані з
пов’язані з ![]() лінійними залежностями, що витікають з (3.4.11).
лінійними залежностями, що витікають з (3.4.11).
Додавши до (3.4.13) часткові розв’язки системи (3.4.4), ![]() та
та ![]() , що залежать від характеру розподілення навантаження (при
, що залежать від характеру розподілення навантаження (при ![]() = const вони теж постійні), приходимо до кінцевих виразів:
= const вони теж постійні), приходимо до кінцевих виразів:
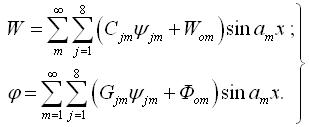 |
(3.4.15) |
Звідси за допомогою (3.2.18), (3.2.20), (3.2.25), (3.2.31) можна отримати вирази для всіх зусиль і переміщень.
Довільні постійні ![]() (а через них і
(а через них і ![]() ) визначаються з граничних умов на краях y = 0 і y = l2, загальним числом 8. Таким чином можуть бути уточнені різні способи закріплення цих країв. Якщо розміри оболонки такі, що значення
) визначаються з граничних умов на краях y = 0 і y = l2, загальним числом 8. Таким чином можуть бути уточнені різні способи закріплення цих країв. Якщо розміри оболонки такі, що значення ![]() і
і ![]() будуть досить великими, то отримаємо, що при у = l2/2
будуть досить великими, то отримаємо, що при у = l2/2 ![]()
![]() (наприклад, при
(наприклад, при 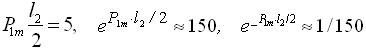 ). Це значить, що взаємний вплив граничних умов на контурі у = 0 і на контурі у = l2 незначний, і тому можна розв’язувати граничну задачу і знаходити довільні постійні для кожного краю окремо. Тоді, наприклад, для краю у = 0 в формулах (3.4.13), (3.4.15) можна відкинути довільні постійні
). Це значить, що взаємний вплив граничних умов на контурі у = 0 і на контурі у = l2 незначний, і тому можна розв’язувати граничну задачу і знаходити довільні постійні для кожного краю окремо. Тоді, наприклад, для краю у = 0 в формулах (3.4.13), (3.4.15) можна відкинути довільні постійні ![]() і
і ![]() . Розрахунок в цьому випадку суттєво спроститься.
. Розрахунок в цьому випадку суттєво спроститься.
Описане в цьому розділі рішення можна використовувати в випадках, коли два протилежні краї оболонки (тобто, у = 0 і у = l2) підкріплено пружними ребрами, а також і тоді, коли є проміжні ребра, що йдуть в тому ж напрямку (в останньому випадку оболонку доводиться ділити на декілька секцій і записувати умови їх спряження). Розв’язання перерахованих задач можна знайти в [23].


