ПОДВІЙНОЇ КРИВИЗНИ
3.4 Розрахунок похилих оболонок подвійної кривизни з більш
складними умовами на контурі
3.4.2 Розрахунок системи, що складається із похилих оболонок і контурних діафрагм (загальний випадок)
3.4.2 Розрахунок системи, що складається із похилих оболонок і контурних діафрагм (загальний випадок)
Тонкостінні просторові покриття, як правило, підкріплюються по контуру діафрагмами. Для похилої оболонки додатної гауссової кривизни це можуть бути арки (рис. 3.4.2, а, б), ферми (рис. 3.4.2, в), криволінійні балки, що оперті на ряд стояків, які хитаються, (рис. 3.4.2, г), або на суцільну стіну (рис. 3.4.2, д).
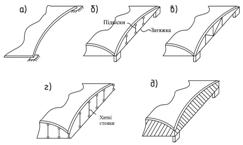
Рисунок 3.4.2 – Контурні кріплення оболонок
Діафрагма, будучи монолітно зв’язаною з оболонкою, деформується разом з нею. Якщо вона являє собою конструкцію, достатньо жорстку в своїй площині і піддатливу із цієї площини (як наприклад схеми на рис. 3.4.2, в, і 3.4.2, д), то таку оболонку допускається наближено розраховувати як шарнірно обперту і використовувати весь розрахунковий апарат, описаний раніше в п. 3.3. Отримані при цьому зусилля на контурі оболонки прикладаються (в зворотному напрямку) до верхнього краю діафрагми, яка на ці зусилля і розраховується. Але для таких діафрагм, як аркові, цей варіант не годиться через велику деформівність у власній площині.
Один із раціональних практичних методів розрахунку похилих оболонок з діафрагмами розроблений В. С. Бартеньовим [6]. Його суть:
І. Для розкриття статичної невизначеності, обумовленої спряженням оболонки з діафрагмою (рис. 3.4.3, а), використовується змішаний метод будівельної механіки. Для країв y=cons за невідомі прийнято:
– зусилля X1(x)=M20(x) і X2(x)=N20(x), що діють по лінії спряження;
– переміщення точок цієї лінії – Z3(x)=Duo(x) і Z4(x)=Dwo (рис. 3.4.3, б).
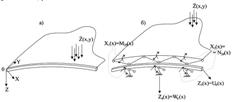
Рисунок 3.4.3 – Спряженість оболонок з діафрагмами
Щоб побудувати основну систему, необхідно:
– вилучити паралельні осі Y зв’язки, що з’єднують оболонку і діафрагму, а також моментні зв’язки;
– накласти на лінію спряження розподілені зв’язки, паралельні осям X і Z.
Таким чином, основна система складається із діафрагми, закріпленої від переміщень в своїй площині, і оболонки, на краю якої рівні нулю М2, N2, v, w. Але тоді оболонка в основній системі стає шарнірно обпертою, як показано на рис. 3.3.1, а тому для знаходження переміщень і зусиль, що виникають в ній від дії зовнішнього навантаження, можна використовувати викладений вище в розділі ІІІ розрахунковий апарат;
ІІ. Вважаємо, що невідомі ![]() , які діють на краю оболонки, що розглядається, не залежать від відповідних невідомих на інших трьох краях.
, які діють на краю оболонки, що розглядається, не залежать від відповідних невідомих на інших трьох краях.
Викликаний ними напружено-деформований стан оболонки зручно описати за допомогою одинарних тригонометричних рядів.
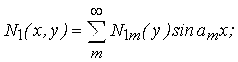

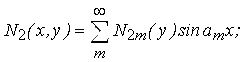

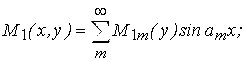
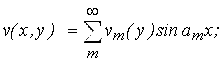
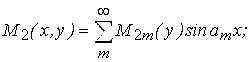

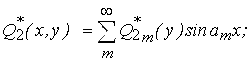
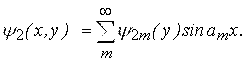
 (3.4.16)
(3.4.16)
Коли ![]() то m1, 3, 5, 7...
то m1, 3, 5, 7...
Коефіцієнти цих рядів залежать від Wm(y) і Фm(y)
ІІІ. Вважають, що для практичних розрахунків можна наближено враховувати тільки m=1, зберігши таким чином в рядах (3.4.16) лише перші члени.
Якщо (3.4.16) розгорнути за допомогою (3.4.15) і (3.4.14), то отримаємо вирази, наведені в табл.1 (індекс m тут і далі опущено).
Позначення в табл.1:
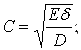
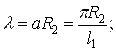
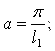
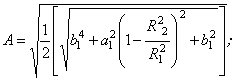
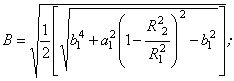  |
(3.4.17) |
Примітки:
| 1) |
(3.4.18) |
2) для сферичної оболонки ![]() ,
,
3) в розрахунках, що тут описуються, коефіцієнт Пуассона прийнятий рівним нулю.
Довільні постійні, що є в наявності в таблиці 3.4.1, визначаються із 4-х граничних умов при у=0.
Як видно із (3.4.14): ![]() ;
; ![]() . (3.4.19)
. (3.4.19)
Крайові значення зусиль і переміщень на основі (3.4.16) і таблиці 1 визначаються:
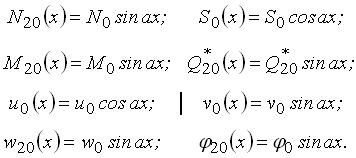 |
(3.4.20) |
Таблиця 3.4.1 – Коефіцієнти в формулах для визначення невідомих
| Зусилля і переміщення | Множник | С1 | С2 | С3 | С4 | ||||
| ψ1 | ψ2 | ψ1 | ψ2 | ψ3 | ψ4 | ψ3 | ψ4 | ||
| N1 | c sin ax | -Б4 | -Б2 | Б2 | -Б4 | Б3 | -Б1 | Б1 | Б3 |
| N2 | -cλ2 cos ax | - | 1 | -1 | - | - | -1 | 1 | - |
| S | -cλ cos ax | d1 | -c1 | c1 | d1 | -d2 | c2 | -c2 | -d2 |
| M1 | λ2 sin ax | 1 | - | - | 1 | 1 | - | - | 1 |
| M2 | -sin ax | -Б2 | Б3 | -Б3 | -Б2 | Б4 | Б3 | -Б3 | Б1 |
| Mk | λ cos ax | -c1 | -d1 | d1 | -c1 | -c2 | -d2 | d2 | -c2 |
| Q2* | c1Б1 +d1Б4 |
-c1Б4 +d1Б1 |
c1Б4 -d1Б1 |
c1Б1 +d1Б4 |
-c2Б2 +d2Б3 |
-c2Б3 -d2Б2 |
c2Б3 +d2Б2 |
-c2Б2 +d2Б3 |
|
| Du | -Б3 | -Б2 | Б2 | -Б3 | Б4 | -Б1 | Б1 | Б4 | |
| Dv | c1Б3 +d1Б1 |
c1Б1 +d1Б3 |
-c1Б1 -D1Б3 |
c1Б3 -d1Б1 |
-c2Б4 -d2Б2 |
c2Б2 -D2Б4 |
-c2Б2 +d2Б4 |
-c2Б4 -d2Б2 |
|
| Dw | 1 | - | - | 1 | 1 | - | - | 1 | |
| Dψ2 | -c1 | -d1 | d1 | -c1 | -c2 | -d2 | d2 | -c2 | |
4) На основі припущення, зробленого в підпункті 2, для кожного краю оболонки окремо потрібно записати систему 4–х рівнянь змішаного методу, з якої і будуть знайдені 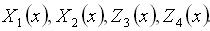 Ці рівняння можна подати в такій формі:
Ці рівняння можна подати в такій формі:
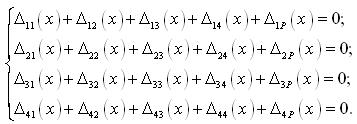 |
(3.4.21) |
Перше з рівнянь виражає рівність нулю кута взаємного обертання оболонки і діафрагми відносно осі Х.
Друге – рівність нулю взаємного переміщення їх в напрямку осі Y, третє – рівність нулю реакцій в накладених зв’язках, направлених повздовж осі Х, четверте – те ж в зв’язках, направлених вздовж осі Z.
В рівняннях (3.4.21) ![]() - D-разове переміщення в напрямку невідомого Хі(х), викликане дією Хк(х) (або Zk(x));
- D-разове переміщення в напрямку невідомого Хі(х), викликане дією Хк(х) (або Zk(x));
![]() – те ж від зовнішнього навантаження; Rik(x) – реакція в зв’язках i-го напрямку, викликана вказаними вище діями;
– те ж від зовнішнього навантаження; Rik(x) – реакція в зв’язках i-го напрямку, викликана вказаними вище діями;
RiР(x) – те ж від зовнішнього навантаження.
Кожну складову в (3.4.21) можна подати у вигляді суми двох величин:
| (3.4.22) |
Перша складова – це D-разове переміщення (або реактивне зусилля) оболонки, а друге – діафрагми.
Щоб привести рівняння (3.4.21) до канонічної форми, всім невідомим по черзі надають одиничні значення, тобто, згідно з (3.4.20), потрібно прийняти
|
(3.4.23) |
В першому випадку розв’язується гранична задача
| M0=1, N0 = u0 = w0 =0, | (3.4.24) |
і визначаються за допомогою таблиці 3.4.1 довільні постійні ![]() а потім D-разове переміщення
а потім D-разове переміщення ![]() і зусилля
і зусилля ![]()
Із (3.4.21) і (3.4.22) зрозуміло, що ці величини являють собою відповідно D-разові одиничні переміщення ![]()
![]() і одиничні реакції
і одиничні реакції ![]() (тут і далі для спрощення пишеться
(тут і далі для спрощення пишеться ![]() а не
а не ![]() ).
).
Згідно з (3.4.20) ці величини можна подати в такій формі:
| (3.4.2)5 |
До подібного вигляду приводяться величини ![]()
![]()
![]()
![]()
Після цього розглядається друга гранична задача
| N0=1, M0 = u0 = w0 =0, | (3.4.26) |
і знаходяться ![]() а за ними -
а за ними - ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Потім розв’язуються третя та четверта задачі:
Потім розв’язуються третя та четверта задачі:
Du0=1, M0 = N0 = w0 =0, Dw0=1, M0 = N0 = u0 =0. |
(3.4.27) |
У вільні члени системи (3.4.21) входять, згідно з (3.4.22), вказані вище переміщення і зусилля на краю шарнірно обпертої оболонки при дії зовнішнього навантаження. Вони визначаються згідно з викладеним у розділі ІІІ в припущенні, що m=1 (при цьому всі подвійні ряди перетворюються в одинарні), і подаються в формі, аналогічній (3.4.25). Нарешті, визначаються і другі складові вільних членів – вантажні переміщення і реактивні зусилля в діафрагмі.
Після підстановки всіх знайдених величин, наприклад, в перше із рівнянь (3.4.21) маємо
Скоротивши на ![]() , отримаємо алгебричне рівняння.
, отримаємо алгебричне рівняння.
На завершення система (3.4.21) набуває вигляду:
(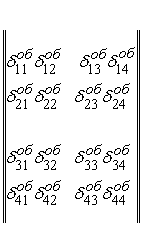 + + 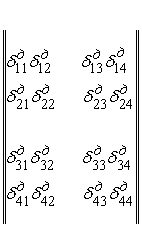 ) × ) × |
(3.4.28) |
Примітка. Перший і четвертий блоки кожної із матриць, що стоять в лівій частині, симетричні, другий і четвертий блоки взаємно транспоновані і мають протилежні знаки.
Розв’язування цієї системи дає значення М0, N0, Du0, Dw0. За ними визначаються постійні ![]() :
:
| (3.4.29) |
Нарешті, за таблицею 3.4.1 обчислюються зусилля і переміщення в оболонці; зусилля в діафрагмі знаходяться за правилами будівельної механіки стержневих систем.
Такий розрахунок потрібно повторити стільки разів, скільки сторін контуру оболонки підкріплено пружними діафрагмами. При цьому рекомендується кожний раз змінювати систему координат, сполучаючи вісь Х з проекцією краю, що розглядається. Обчислені зусилля і переміщення додаються до відповідних величин, знайдених для основної системи (тобто, шарнірно обпертої (articulated about) оболонки) при дії на неї зовнішнього навантаження.


