Якщо діафрагма має дуже малу жорсткість із власної площини, то можна вважати, що вона не сприймає ні згинального моменту, ні нормальної сили. Тому для краю х=0 буде

і тоді потрібно шукати лише  Du₀  і  Dw₀, тобто задача про спряження розв’язується методом переміщень. Система (3.4.21), а відповідно і (3.4.28), значно спрощуються, (3.4.28) набирає вигляду

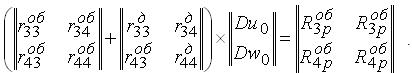(3.4.30)

Із одиничних станів (3.4.23) потрібно розглядати лише третій і четвертий. Нижче наведена збірка формул для цього випадку:

    

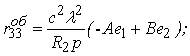
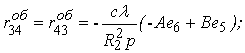
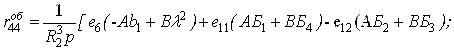(3.4.31)

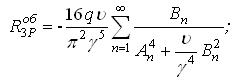                 (n=1,3,5,7,…)

(3.4.32)

                            

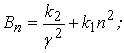
  визначається з таблиці 3.4.2.

Таблиця 3.4.2  – Значення коефіцієнтів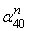

γ		γ		γ		γ
0,3	0,354	0,6	0,686	1	0,982	1,667	1,164
0,4	0,470	0,75	0,821	1,25	1,081	2,0	1,194
0,5	0,582	0,8	0,859	1,333	1,104	2,5	1,215
						3,333	1,227

Якщо діафрагма являє собою кругову арку з затяжкою (рис. 3.4.2), то

    ,

.

    ;            

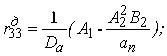
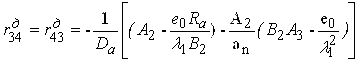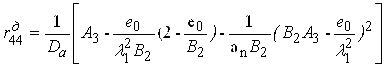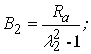
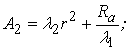
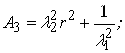
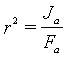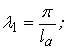
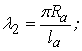
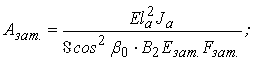
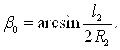                                 (3.4.33)

де – прогін арки і радіус її осі;

е₀ – відстань від осі арки до серединної поверхні оболонки;

Е – модуль пружності матеріалу оболонки і арки;

– те ж матеріалу затяжки;

,  – площі поперечних перерізів арки і затяжки;

J – момент інерції перерізу оболонки одиничної ширини;

J_а – момент інерції арки.

Довільні  постійні     обчислюють за формулами (3.4.34)

;      ;

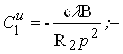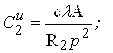(3.4.34)

            

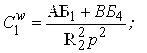
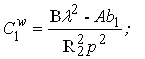
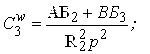
а потім підставляють у вираз (3.4.29). Далі за допомогою таблиці 3.4.1 обчислюють зусилля і переміщення в оболонці.

Щоб знайти зусилля в арковій діафрагмі, достатньо прикласти до неї краєві зусилля    і   та виконати розрахунок будь-яким із методів будівельної механіки стержневих систем.

Якщо діафрагма являє собою двошарнірну арку (рис. 3.4.2, а), то в (3.4.33) потрібно прийняти ;  якщо вона така, як на рис. 3.4.2, г,  приймаємо  і залишаємо в системі (3.4.29) лише перше рівняння.