 |
|---|
10 ОДНОМІРНІ ТЕЧІЇ ГАЗУ
10.3 Приклади
10.3.1. Визначити необхідний внутрішній діаметр димової труби висотою Н = 120 м для видалення гарячих газів при масовій втраті G =100 кг/с. Температура зовнішнього повітря t=20 °С, барометричний тиск у поверхні землі Pa = 1,026?105 Па. Температура гарячих газів t1 = 250 °C, початковій їх тиск P1 = 0,997 бар, густина газів rг= 1,295 кг/м3 при t0 = 0 °С і Р0 = 100 кПа. Шорсткуватість внутрішньої поверхні труби ke = 2 мм.
Розв’язок
Враховуючи незначну зміну тиску і густини газів на вході і виході із труби, скористаємось рівнянням Бернуллі без врахування стисливості.
Тиск на виході із труби
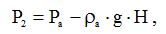
Початкова густина гарячих газів
В подальшому використовуємо метод підбору, для цього приймаємо три значення діаметра димової труби d1 = 3 м, d2 = 4 м, d3 = 5 м.
Для цих значень середня середня швидкість гарячих газів в трубі, враховуючина всьому протязі труби,
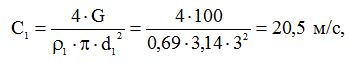
аналогічно
Відповідно числа Рейнольдса
.
На границі змішаного і шорсткуватого тертя:
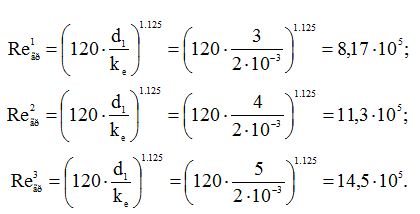
У двох перших випадках Re>Reгр. і для визначення гідравлічного коефіцієнту тертя використаємо формулу Мурина
,
.
Оскількито використовуємо формулу Альтшуля
.
Враховуючи, що при початковому тиску
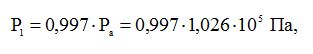
швидкість газів v1=0, залишимо рівняння Бернуллі для початкового і кінцевого перерізів газового потоку:
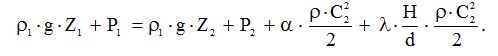
І оскільки Z1 – Z2 = H, то
.
Враховуючи, що
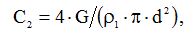
маємо
.
Останнє рівняння розв’язуємо графоаналітичним методом, маючи на увазі що задане
Результати розрахунків кривоїзводимо в таблицю
п\п
d, м
,Па
1
2,8
0,0177
0,0287
1330
2
3
0,178
0,021
1169
3
4
0,0167
0,00586
911
4
5
0,0162
0,0222
849
Далі будуємо залежність
і знаходимо d = 2,92м (рис.10.3)
10.3.2. В сталевому трубопроводі діаметром d=0,1м і довжиною l = 100 м подається стисле повітря під тиском абсолютним Р1=900 кПа. Температура повітря t = 20 оС. Швидкість на початку трубопровода С1 = 30 м/с. Визначити масову витрату повітря G і тиск в кінці труби Р2. Кінематична в’язкість повітря
Абсолютна шорсткуватість стінок трубопровода kе=0,3 мм.
Розв’язок
Густина повітря на початку труби
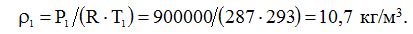
Масова втрата стислого повітря
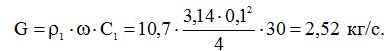
Число Рейнольдса
.
Відносна шорсткуватість
.
Коефіцієнт гідравлічного тертя
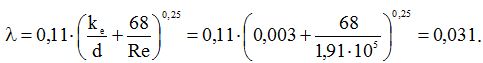
Тиск в кінці трубопровода знаходимо за формулою
;
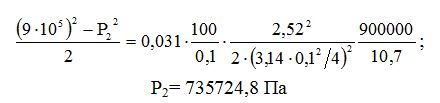
P2= 735724,8 Па