3 КІНЕМАТИКА РІДИНИ

3.4 Потенціал швидкості, функція току

Кутова швидкість обертання рідинної частинки
                                          (3.22)
 
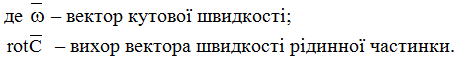
В проекціях на декартові вісі координат
                                 (3.23)
При потенційному (безвихровому) русі вектор
                                            (3.24)
в координатній формі запишеться так
                                     (3.25)
В потенційному полі існує скалярна функція j, яка зв’язана з вектором швидкості такою залежністю
                                           (3.26)
Ця функція називається потенціалом швидкості. Приймаючи до уваги потенціал швидкості для плоскої течії, визначимо проекції швидкості із наступних співвідношень
                                      (3.27))
Криві j(х, у) = const називаються еквіпотенційними лініями.
Рівняння нерозривності для потенційного руху нестисливої рідини перетворюється в рівняння Лапласа
                                           (3.28)

для плоскої течії
                                        (3.29)
Отже потенціал швидкості є гармонічною функцією.
Для плоского потоку нестисливої рідини існує функція y(х, у), яка називається функцією струменя, для якої справедливі умови
                                     (3.30)
Вираз y(х, у) = const є рівнянням сімейства ліній струменів.
Для безвихрового руху функція струменя, як і потенціал швидкості, задовольняє рівнянню Лапласа
                                       (3.31)
Різниця значень функцій струменя на двох суміжних лініях струменя дорівнює витраті між ними, тобто
                                        (3.32)
Функції j і y визначаються із співвідношень
                                   (3.33)
які є умовними Коші-Рімана. Вони показують, що лінії взаємно ортогональні.
Для розв’язання практичних задач широко використовується метод накладання потенціальних потоків, які є слідством лінійності рівнянь Лапласа.
Дійсно, якщо є два потоки з потенціалами то потенціал швидкості нового результуючого потоку
                                         (3.34)
Аналогічно функція струменя буде дорівнювати алгебраїчній сумі функцій струменів вихідних потоків
                                         (3.35)