3 КІНЕМАТИКА РІДИНИ

3.5 Приклади

           3.5.1. Визначити масову витрату гарячої води в трубопроводі з внутрішнім діаметромякщо відомо, що середня швидкість води    V = 3 м/с, а густина
Розв’язок
Так як через любий переріз трубопроводу за 1 с протікає води
                        
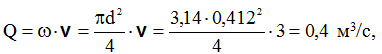
то масова витрата води розраховується як
                                 

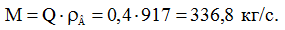
           3.5.2. Визначити рівняння лінії току, а також траєкторію частинки, яка проходить в момент часу через точку простору з координатами
Поле швидкостей газу задано проекціями
                                        

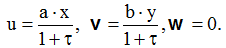
Розв’язок
Диференційне рівняння траєкторії руху частинки
                                             
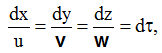
а для заданого поля швидкостей
                                    
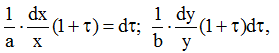
звідкіля
                                       
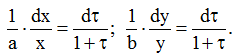
Проінтегрувавши, маємо
                         
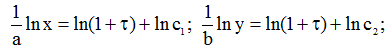
або
                                   
                                   
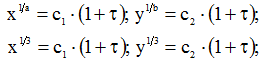
довільні сталі інтегрування знаходимо із початкових умов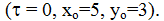

Підставивши ці значення, маємо
                                              

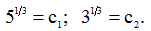
Виключаємо час, знаходимо рівняння траєкторії
                      
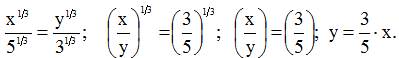
Для знаходження лінії току використовуємо рівняння . Для заданого поля швидкостей
                                                  
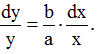
Після інтегрування
                      
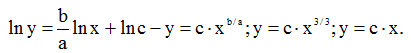
Для лінії току, яка проходить через точку , довільна стала
Поле швидкостей нестаціонарне, але лінія току і траєкторія співпадають. Це тому, що з часом швидкість змінюється лише за величиною, а не за напрямком, тобто одиничний вектор поля швидкостей не залежить від часу.

           3.5.3. Визначити прискорення рідинної частинки в точці А з координатами x = d, y = e, z = g (x, y, z в метрах) в момент . Задані проекції швидкостей рідинних частинок

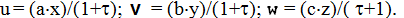
Розв’язок
Записуємо вираз для компоненти прискорення
                                    
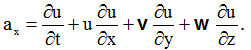
З врахуванням значення  u  маємо
            
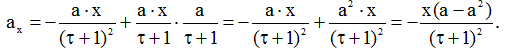
Аналогічно для
            
             
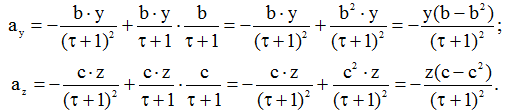
Повне прискорення частинки
       
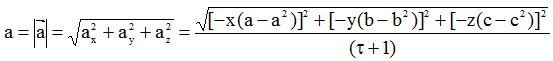
в момент часу t = 3 для точки А маємо
               
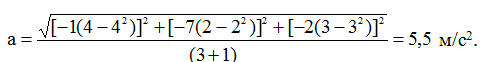
           3.5.4. Чи може поле швидкостей нестисливої рідини мати потенціал:
Розв’язок
Плоский потік нестисливої рідини має потенціал швидкості j , який повинен задовольняти рівняння Лапласа
                                           
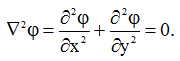
Поле швидкостей нестисливої рідини може мати потенціал 1, оскільки
                     
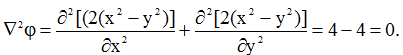
і не може мати потенціал 2, оскільки
                        
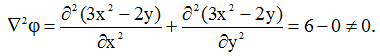
           3.5.5. Визначити, при якому значенні коефіцієнта b можливі течії нестисливої рідини з такими проекціями поля швидкостей: а) u = bx, V=by; б) u=2bx, V = -2by. Визначити характер можливих течій.
Розв’язок
Коли рухається нестислива рідина, належить виконання рівнянн нерозривності

Отже, u = 0, V = 0, тобто рух відсутній.
У другому випадку:
Ця умова виконується при любому значенні коефіцієнта b.
При течія потенційна.
Визначаємо лінії течії
                                   
            
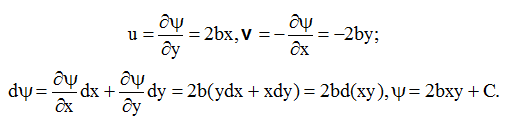
Визначаємо еквіпотенційні лінії току