 |
|---|
3 КІНЕМАТИКА РІДИНИ
3.6 Завдання на СРС
3.6.1. По трубопроводу подаєтьсяВизначити діаметр трубопроводу, якщо швидкість води дорівнює 2 м/с.
Відповідь: d = 0,445 м.3.6.2. Одержати вираз для проекцій локальних прискорень рідинної частинки, якщо рівняння руху мають вигляд
Відповідь:3.6.3. Визначити прискорення рідинної частинки, якщо поле задано проекціями швидкостей:
Відповідь:3.6.4. Визначити прискорення рідинної частинки в точці простору з координатами х = 3, у = 2, z = 1, якщо поле задано проекціями швидкостей
Відповідь:3.6.5. Рух нестисливої рідини заданий проекціями швидкостей
Встановити вигляд виразу для проекції швидкості на вісь х, якщо на початку координати u = 2.
Відповідь: u = х + 2.3.6.6. Рух задано проекціями швидкостей
Знайти рівняння лінії току, а також траєкторію частинки, яка проходить в момент часу t=0 через точку простору з координатами х = a, y = b.
Відповідь: Рух частинок відбувається по еліпсуде лінія
3.6.7. Перевірити можливість існування руху нестисливої рідини для поля, яке задане проекціями швидкостей
Відповідь: Рух можливий.3.6.8. Визначити швидкість обертання рідинної частинки в точці простору з координатами x = 3, y = 2, z = 0, якщо поле задано проекціями швидкостей u = 2xy, V = 4yz, w = 2xz.
Відповідь:3.6.9. Одержати вираз для лінії току, якщо проекції швидкостей
u = xy, V = -2x(x–1).
Відповідь:Лінії току еліпси, вісі яких перетинаються в точці (1, 0).
3.6.10. Знайти рівняння для лінії току, яка проходить через точку з координатами x=1, y=-1, z=2, якщо проекції швидкостей u=x, V=-y, w=-2z.
Відповідь:3.6.11. Чи може поле швидкостей нестисливої рідини мати потенціали, якщо:
Відповідь:Лінії току - концентричні кола, які відповідають потенціальному вихору.
3.6.12. Знайти рівняння лінії току, а також траєкторію частинки, яка проходить в момент часу t = 0 через точку простору з координатами х = с і у = d, якщо поле швидкостей газу задано проекціями
Остання цифра шифру
0
1
2
3
4
5
6
7
8
9
а
2
3
4
5
6
7
8
9
3
4
b
1
2
3
4
5
6
7
8
9
2
Передостання цифра шифру
0
1
2
3
4
5
6
7
8
9
c
3
5
7
9
8
7
6
5
4
3
d
4
6
8
8
7
6
5
4
3
2
3.6.13. Визначити прискорення рідинної частинки в точці А з координатами х = d, у = e, z = g в момент часу t по заданих проекціях швидкостей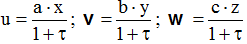
Остання цифра шифру
0
1
2
3
4
5
6
7
8
9
а
1
2
3
4
1
2
3
4
5
6
b
3
1
2
2
4
5
4
3
2
1
c
2
3
5
6
3
3
5
2
3
4
Передостання цифра шифру
0
1
2
3
4
5
6
7
8
9
d
1
2
3
4
5
6
7
8
9
1
e
8
7
6
5
4
3
2
1
2
4
g
2
3
4
6
3
4
5
4
5
7
t
2
3
4
5
6
7
8
9
1
2
3.6.14. Визначити швидкість руху рідини за величиною та напрямом в точці М з координатами х, у, якщо рух є результатом складання двох течій, для яких задані відповідні потенціали швидкостейВизначити траєкторію частинок.
Остання цифра шифру
0
1
2
3
4
5
6
7
8
9
а
1,5
2,5
3,5
4,5
5,0
5,5
6,0
6,5
7,0
8,0
Передостання цифра шифру
0
1
2
3
4
5
6
7
8
9
b
1
2
3
4
5,2
6,2
7,2
1,6
1,8
2,9