3.1 Вихідні передумови Фур’є-інтегрального методу ідентифікації

Відомо, що сигнал x(t), який діє на вході лінійної динамічної системи з імпульсною перехідною характеристикою g(t) (див. рис. 1.6), та реакція системи y(t) на цей сигнал пов’язані між собою інтегралом згортки (1.13), який для зручності посилання наведемо й у цьому розділі під номером (3.1)

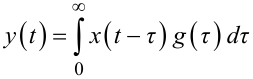(3.1)

або у більш загальному вигляді:

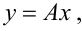(3.2)

де A — оператор системи.

Якщо моделі сигналів подати у вигляді рядів Фур’є з одним і тим же спектром частот, то кожну гармонічну складову сигналу x(t) можна однозначно пов’язати із гармонічною складовою тієї ж частоти сигналу y(t) алгебраїчним виразом, який містить у собі тільки коефіцієнти Фур’є сигналів x(t), y(t) та спектральні складові АФЧХ W(jω) системи на цій же частоті.

Які ж задачі можна розв’язувати за допомогою отриманих алгебраїчних виразів, використання яких у певних комбінаціях та у певній послідовності і являє собою Фур’є-інтегральний метод ідентифікації (ФІМІ) сигналів та систем?

Таких задач дві

Задача ідентифікації системи. У цій задачі, відштовхнувшись від параметричного аналізу відомих сигналів x(t) та y(t), синтезується такий оператор системи A, який оптимальним чином (за деяким критерієм) віддзеркалює властивості системи як перетворювача сигналу x(t) у сигнал y(t).

Задача ідентифікації (відновлення) вхідного сигналу. Для розв’язання цієї задачі за допомогою ФІМІ синтезуються такі співвідношення, виходячи з яких за відомим вихідним сигналом y(t) і заданим оператором A системи ідентифікуються (відновлюються) характеристики сигналу x(t), який, подіявши на вхід цієї системи, викликав реакцію y(t).

Виконанням же яких умов повинно супроводжуватись використання ФІМІ, або, що одне і те ж, якими ж повинні бути вихідні передумови?

Для лінійних динамічних систем така передумова лише одна — сигнали x(t), y(t) повинні задовольняти умови Діріхле, щоб їх можна було розкласти у ряди Фур’є.

Ця передумова у реальних динамічних системах, запаси енергії в яких завжди обмежені, а тому амплітуди сигналів не можуть бути нескінченними, виконується завжди.