3.2 Синтез алгоритмів параметричної ідентифікації сигналів на вході лінійної вимірювальної системи

У більшості вимірювальних систем мають місце процеси перетворення енергії, якщо не впродовж усього каналу вимірювання, то, принаймні, хоча б на одній з його ділянок, а тому, розв’язуючи задачу синтезу алгоритмів параметричної ідентифікації сигналів на вході вимірювальної системи, залишаємось у визначеній у цьому посібнику області ідентифікації динамічних систем.

Як відомо, у вимірювальних системах використовується лише лінійний відрізок характеристики «вхід — вихід», тобто їх без будь-яких натяжок відносять до класу лінійних динамічних систем

Зосередженість параметрів вимірювальних систем теж не викликає сумнівів за умови, що до їх складу не відносять канал передачі вимірювальної інформації на значну відстань (про такі канали мова йтиме в 3-й частині посібника).

Для вимірювальних систем визначеного класу справедливим є інтегральне рівняння згортки (3.1).

Якщо відрізок часу спостереження вихідного сигналу y(t) дорівнює T, його можна подати на цьому відрізку у вигляді ряду Фур’є

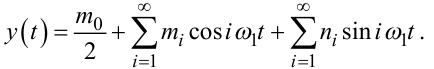(3.3)

Не накладаючи умови — відомий, чи ні, нам вхідний сигнал x(t) - подамо його у вигляді ряду Фур’є на тому ж відрізку часу T:

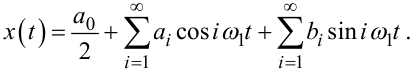(3.4)

У виразах (3.3), (3.4)

— коефіцієнти Фур’є сигналів xt, yt, які знаходяться за відомими фор- мулами:

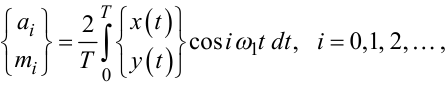(3.3)

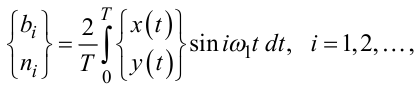(3.6)

де 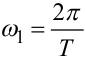— частота першої гармоніки

Підставляючи ряди (3.3) та (3.4) в інтеграл згортки (3.1), після низки нескладних перетворень, отримаємо

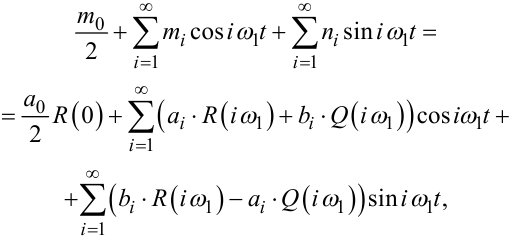(3.7)

де R(iω₁), Q(iω₁) — значення, відповідно, дійсної R(ω) та уявної Q(ω) частотних характеристик вимірювальної системи на частотах iω₁, i = 0,1, 2,... .

Оскільки вираз (3.7) — це тотожність, то справедливими є, по-перше, рівняння

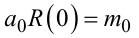(3.8)

для постійних складових a₀, m₀ сигналів x(t), y(t), а, по-друге, система рівнянь

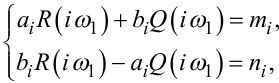(3.9)

де i = 1, 2,... для всіх інших коефіцієнтів Фур’є a_i, b_i, m_i, n_i сигналів x(t), y(t).

З теорії рядів Фур’є та властивостей уявної частотної характеристики Q (ω) відомо, що

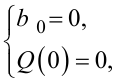(3.10)

а тому рівняння (3.8) теж можна отримати із системи (3.9) при i = 0. Тож у подальшому будемо розглядати лише систему рівнянь (3.9), поклавши в ній: i = 0, 1, 2,... .

Розв’яжемо цю систему відносно a_i, b_i. Отримаємо:

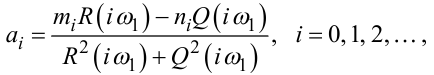(3.11)

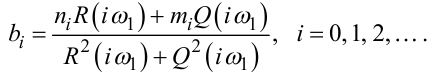(3.12)

Далі розв’язання задачі ідентифікації вхідного сигналу x(t) вимірювальної системи можна здійснювати, використовуючи один із двох підходів.

Під час використання першого з підходів, який назвемо прямим, алгоритм розв’язання задачі містить такі етапи: спочатку за реалізацією вихідного сигналу y(t), зафіксованою на відрізку часу T, за допомогою формул (3.5) і (3.6) визначаємо коефіцієнти Фур’є m_i, n_i цього сигналу для значень i = 0,N. Потім для цих же значень i за заданими частотними характеристиками R(ω), Q(ω) вимірювальної системи визначаємо їх значення на частотах iω₁, тобто R(iω₁), Q(iω₁). Підставляючи m_i, n_i, R(iω₁), Q(iω₁) у формули (3.11), (3.12), отримаємо для кожного значення i із множини 0,N пару коефіцієнтів Фур’є a_i, b_i вхідного сигналу x(t).

Підстановкою всіх цих коефіцієнтів в зрізаний ряд (3.4) і завершуємо розв’язання задачі ідентифікації (відновлення) вхідного сигналу x(t) за вихідним сигналом y(t) вимірювальної системи за допомогою прямого алгоритму.

У цьому алгоритмі залишилось нез’ясованим одне важливе питання — а яку ж кількість гармонічних складових необхідно взяти в зрізаному ряді (3.4)?

Іншими словами, яку потужність N повинна мати множина коефіцієнтів Фур’є параметрично ідентифікованого сигналу x(t)?

Для отримання відповіді на це питання використаємо встановлену математиками закономірність, яка полягає у тому, що коефіцієнти Фур’є довільного сигналу спадають у порядку, обернено пропорційному своєму номеру. Це означає, що спектр Фур’є сигналу складають лише ті коефіцієнти, які задовольняють цю властивість.

Всі інші коефіцієнти Фур’є, що мають номери вищі від того, для якого порушується вищеозначена умова, складають спектр завади.

Таким чином, число N гармонічних складових у вхідному сигналі x(t) необхідно залишити, виходячи з того, на якому коефіцієнті починає порушуватись умова обернено пропорційного спаду коефіцієнтів Фур’є за порядком величини відносно свого номера.

Розглянутий прямий алгоритм ідентифікації вхідного сигналу x(t) вимірювальної системи не можна віднести до класу оптимальних, оскільки під час його побудови не був використаний ніякий критерій оптимальності. Крім того, запропонований спосіб вибору потужності N множини коефіцієнтів Фур’є сигналу x(t) дає, у загальному випадку, «розмите» значення цього числа.

Більш ефективний розв’язок поставленої задачі можна отримати, використовуючи другий підхід, який базується на алгоритмі оптимального відновлення сигналу x(t).

Під час побудови оптимального алгоритму задачу відновлення також будемо розв’язувати, виходячи з рівнянь (3.9), але скористаємось ними не для отримання розрахункових співвідношень (3.11), (3.12), а для побудови критеріїв оптимальності:

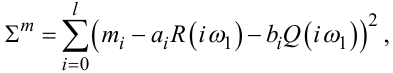(3.13)

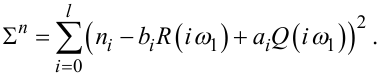(3.14)

Із цих виразів видно, що коефіцієнти a_i, b_i входять в кожне із критеріальних співвідношень (3.13), (3.14), а тому одне з них можна використати для чисельного визначення значень коефіцієнтів a_i, b_i вхідного сигналу x(t), а друге — для визначення їх оптимальної кількості N .

Покажемо, як це зробити.

Візьмемо частинні похідні за a_i, b_i, i = 0,l від ∑^m і прирівняємо їх нулю. Отримаємо систему 2l + 1 нормальних рівнянь Гаусса

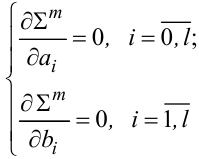(3.15)

для визначення 2l + 1 оцінок коефіцієнтів a₀; a₁, b₁; ... ; a₁ , b₁ , які позначимо індексними зірочками, тобто

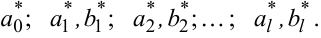(3.16)

Розв’язавши систему алгебраїчних рівнянь (3.15) одним із стандартних методів, отримаємо чисельні значення оцінок вищеозначених коефіцієнтів.

Підставивши знайдені шляхом розв’язання системи (3.15) оцінки коефіцієнтів (3.16) у вираз (3.14), в який підставимо також знайдені раніше коефіцієнти Фур’є n_i, i = 0,l вихідного сигналу y(t), визначимо чисельне значення ∑ⁿ, яке позначимо .

Використовуючи ще один коефіцієнт Фур’є m_l+1 вихідного сигналу y(t) додамо до системи рівнянь (3.15) ще два рівняння

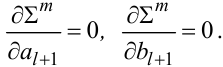(3.17)

Розв’язавши систему рівнянь (3.15), (3.17), отримаємо нові оцінки коефіцієнтів a_i, b_i, а також оцінки коефіцієнтів a_l+1, b_l+1, які раніше не визначались.

Підставивши знайдені тепер уже шляхом розв’язання системи рівнянь (3.15), (3.17) оцінки всіх отриманих коефіцієнтів Фур’є вхідного сигналу x(t) та значення коефіцієнтів n_i, i = 0,l+1 вихідного сигналу y(t) у вираз (3.14), в якому верхню границю суми замінено з l на l + 1, отримаємо нове чисельне значення ∑_n, яке позначимо .

Повторюючи наведену вище процедуру для l + 2, l + 3, ..., l + q , отримаємо відрізок числового ряду

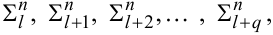(3.18)

найменший член якого

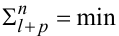(3.19)

визначає, згідно з основною ідеєю методу найменших квадратів, оптимальну кількість

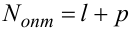(3.20)

членів ряду Фур’є у виразі (3.4), яким задається математична модель вхідного сигналу x(t).

У цій процедурі залишається нез’ясованим тільки одне питання: як вибрати значення l, з якого повинен починатись відрізок ряду (3.18)?

Для відповіді на це питання скористаємось критерієм спаду коефіцієнтів

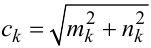(3.21)

вихідного сигналу y(t) за порядком, обернено пропорційним своєму номеру k, про який вже йшла мова під час розгляду прямого алгоритму розв’язання задачі параметричної ідентифікації вхідного сигналу x(t).

Визначивши номер k коефіцієнта Фур’є c_k, для якого порушується вищеозначена умова, необхідно взяти значення l на 2–3 одиниці менше, тобто

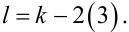(3.22)

Таке зміщення вліво початку процедури пошуку оптимальної кількості N_опт членів ряду Фур’є у моделі сигналу x(t) забезпечує надійний і однозначний розв’язок задачі оптимального відновлення цього сигналу на множині коефіцієнтів Фур’є, які параметрично визначають даний сигнал.

• Порівнюючи алгоритми прямого і оптимального відновлення вхідного сигналу x(t) вимірювальної системи за відомою її реакцією y(t) на цей сигнал, можна відзначити:

внаслідок незалежності обчислення кожного коефіцієнта Фур’є алгоритм прямого відновлення потребує об’єму пам’яті комп’ютера на 1–2 порядки меншого за той, який потрібен для реалізації оптимального алгоритму, котрий містить у собі процедуру розв’язання системи алгебраїчних рівнянь, порядок якої дорівнює числу необхідних для оптимальної параметричної ідентифікації сигналу x(t) коефіцієнтів Фур’є;

• завдяки оптимальній процедурі пошуку кількості членів ряду Фур’є, яка забезпечує однозначно момент зупинки процесу побудови оптимальної моделі сигналу x(t), оптимальний алгоритм відновлення розв’язує задачу із суттєво вищою точністю;

• і прямий, і оптимальний алгоритми розв’язують задачу відновлення вхідного сигналу x(t) лише тоді, коли ширина частотного спектра вимірювальної системи більша ширини частотного спектра цього сигналу — лише у цьому випадку кожна гармонічна складова вхідного сигналу x(t) знайде своє віддзеркалення у вихідному сигналі y(t), і жодна з них не буде відфільтрована вимірювальною системою