3.3 Побудова алгоритму параметричної ідентифікації лінійної динамічної системи за допомогою ФІМІ

Якщо задача відновлення сигналів x(t) та y(t, які фіксуються, відповідно, на вході та на виході лінійної динамічної системи, розв’язана за допомогою ФІМІ, то найбільш ефективним методом синтезу параметричної мате- матичної моделі цієї системи є також ФІМІ.

Ефективність цього методу обумовлена перш за все тим, що коефіцієн- ти Фур’є вихідних сигналів x(t), y(t) інформаційно-вимірювальних систем, встановлених на вході і виході динамічної системи, що ідентифікується, які відновлюються за допомогою ФІМІ, можуть бути безпосередньо використаними і під час розв’язання задачі ідентифікації цієї ж динамічної системи цим же методом, а тому і етап відновлення сигналів, і етап ідентифікації системи можуть бути реалізовані в одній і тій ж мікропроцесорній системі обробки вимірювальної інформації. Це суттєво зменшує кількість апаратних засобів, необхідних для реалізації обох задач, та час, який витрачається на розв’язання, особливо у випадках, коли для обчислення коефіцієнтів Фур’є використовуються методи швидкого перетворення Фур’є.

Всі перетворення (до отримання виразів (3.9), (3.10) включно), здійснені у попередньому підрозділі, залишаються справедливими і під час побудови алгоритму ідентифікації динамічної системи, для якої x(t) є вхідним сигналом, а y(t) — вихідним.

Із системи рівнянь (3.9), (3.10) випливає, що

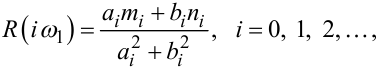(3.23)

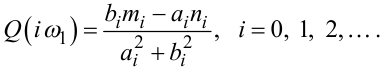(3.24)

Отриманням формул (3.23), (3.24) закінчується перший етап побудови алгоритму параметричної ідентифікації динамічної системи за допомогою ФІМІ.

На другому етапі будемо шукати математичну модель системи, дійсна R(ω) та уявна Q(ω) частотні характеристики якої в окремих точках визначаються співвідношеннями (3.23), (3.24) у класі передаточних функцій виду

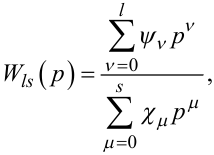(3.25)

де ψ_ν, χ_μ — параметри, числові значення яких потребують визначення у процесі ідентифікації. Нагадаємо, що для динамічних систем, які можна фізично реалізувати, завжди

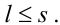(3.26)

Критеріальне співвідношення

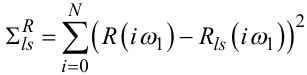(3.27)

будемо використовувати для пошуку оптимальних числових значень параметрів ψ_ν, χ_μ передаточних функцій W_ls (p) вибраної структури, тобто, за заданих значень l і s, а критеріальне співвідношення

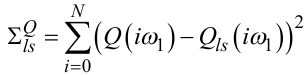(3.28)

— для оптимізації процесу вибору структури цієї передаточної функції, тобто, для визначення оптимальних значень l і s.

У (3.27), (3.28) R_ls (iω₁), Q(iω₁) — функціонально задані, виходячи з вибраної структури передаточної функції W_ls (p), у точках iiω₁ (i = 0,1, 2,...) вирази для дійсної R_ls (iω) і уявної Q_ls (iω) частотних характеристик об’єкта, що ідентифікується, для отримання яких слід використати відомі з теорії автоматичного керування та першого розділу цього посібника співвідношення:

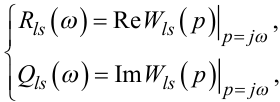(3.29)

а R (iω₁), Q (iω₁) — розв’язки рівнянь (3.23), (3.24).

Використовуються співвідношення (3.23) — (3.29) у процесі параметричної ідентифікації динамічної системи у такій послідовності: задаючись у (3.25) різними конкретними значеннями l і s так, щоб виконувалась умова фізичної реалізованості (3.26), для кожної конкретної пари значень l і s за співвідношеннями (3.29) визначаємо функції R_ls (iω) та W_ls (iω). У результаті цієї операції отримуємо множину пар частотних характеристик

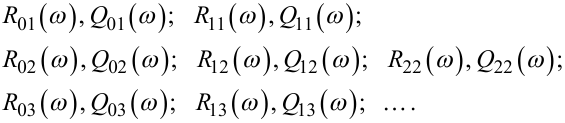(3.30)

Підставивши по черзі функції R₀₁(iω), R₁₁(iω), R₀₂(iω), R₁₂(iω), ... із множини (3.30), задані у точках iω₁, разом із значеннями R(iω₁), взятими з (3.23), у критеріальне співвідношення (3.27), і здійснивши відносно (3.27) стандартну процедуру методу найменших квадратів, визначимо оптимальні за критерієм мінімуму суми квадратів відхилень оцінки коефіцієнтів ψ_ν, χ_μ передаточних функцій виду (3.25) для кожної конкретної пари значень l і s із наперед заданого діапазону.

Для того, щоб оптимізувати структуру передаточної функції W_ls(p) системи, що ідентифікується, підставимо найдені з використанням функції R_ls(ω) за допомогою методу найменших квадратів числові значення коефіцієнтів ψ_ν, χ_μ, у відповідні вирази для Q_ls(ω) із множини пар (3.30). Конкретизовані у такий спосіб функції Q_ls(ω), у свою чергу, підставимо у друге критеріальне співвідношення (3.28). Після підстановки у (3.28) також і значень Q(iω₁), отриманих із (3.24), і прямих обчислень значень побудуємо числовий ряд

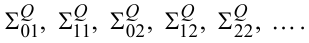(3.31)

Виходячи із основної ідеї методу найменших квадратів, можна стверджувати, що та пара характеристик Rls , Qls  , яка задає найменший член

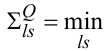(3.32)

ряду (3.31), і визначає оптимальну структуру математичної моделі динамічної системи, що ідентифікується.

Під час розгляду цього алгоритму привертає до себе увагу той факт, що на відміну від оптимального алгоритму відновлення сигналу, побудованого у попередньому підрозділі, в ньому не виникає запитання про кількість гармонічних складових, які треба утримувати в зрізаних рядах Фур’є сигналів x(t), y(t), оскільки відповідь на це питання однозначна — чим більше, тим краще, але кількість їх обов’язково повинна бути більшою від числа коефіцієнтів передаточної функції W_ls(p), які нам потрібно визначити у процесі ідентифікації системи.

Але у цій задачі потрібно мати відповідь на інше запитання, а саме: за яких умов задача ідентифікації лінійної динамічної системи за допомогою ФІМІ може бути віднесена до класу коректних і мати однозначний розв’язок?

Для відповіді на це запитання нагадаємо, що задача ідентифікації лінійної динамічної системи у частотній області з використанням інформації про вхідний x(t) та вихідний y(t) сигнали може бути розв’язана лише за умови, що спектр Фур’є вхідного сигналу є ширшим частотного спектра системи. У цьому випадку кожна частота спектра системи може бути збуджена відповідною складовою спектра вхідного сигналу і у тій чи іншій мірі проявити себе у спектрі вихідного сигналу.

Якщо ж частотний спектр вхідного сигналу є вужчим, ніж спектр системи, то деякі частоти спектра системи не будуть збуджені і не проявлять себе у спектрі вихідного сигналу, а тому вони не зможуть бути ідентифікованими жодним із частотних методів.

Тож, як висновок із наведеного вище аналізу, випливає, що задача параметричної ідентифікації лінійної динамічної системи за допомогою ФІМІ розв’язується однозначно лише тоді, коли коефіцієнти Фур’є вихідного сигналу цієї системи спадають швидше коефіцієнтів Фур’є її вхідного сигналу.