3.4 Екскурс у метод найменших квадратів

Під час реалізації алгоритмів оптимальної параметричної ідентифікації сигналів та систем, розглянутих у попередніх підрозділах цього розділу, використано метод найменших квадратів (МНК), ідея якого належить Гауссу.

І хоча виклад основ МНК можна знайти у посібниках із математичної статистики та обробки результатів експериментів, доцільно подати їх у цьому посібнику також. Оскільки, по-перше, його використання є невід’ємною частиною Фур’є-інтегрального методу ідентифікації, змістом якого заповнено саме цей розділ, а по-друге, використання МНК має певні обмеження, на які автори багатьох посібників не звертають увагу студентів, що у подальшому може стати джерелом помилок в їх дослідженнях, обробка результатів яких здійснюється з використанням МНК. В цьому посібнику ці обмеження не лише показано, але й висвітлено можливі наслідки їх ігнорування.

Після цього коротенького вступу перейдемо до викладу безпосередньо МНК.

Нехай відомо, що вихідний параметр процесу, який вивчається, позначимо його y, лінійно залежить від вхідного параметра x (суцільна пряма лінія на рис. 3.1).

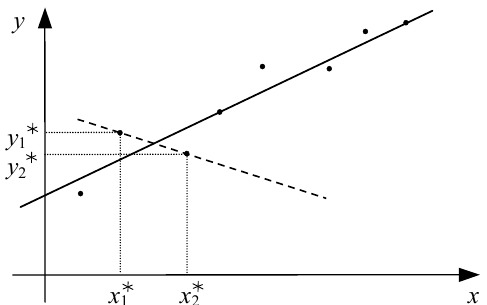
Рисунок 3.1 — Графічна інтерпретація причин, які обумовлюють необхідність використання МНК

Тобто припустимо, що статична характеристика цього процесу може бути подана у вигляді

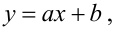(3.33)

де a і b — коефіцієнти, для визначення числових значень яких необхідно, як мінімум, задати два значення x₁, x₂ вхідній величині x і заміряти відповідні їм значення y₁, y₂ вихідної величини y, оскільки лише під час виконання цих умов для моделі (3.33) можна скласти систему двох алгебраїчних рівнянь із двома невідомими a і b

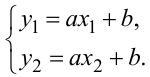(3.34)

Але результати будь-яких експериментальних вимірювань несуть у собі похибки, обумовлені класом точності вимірювальних засобів, дією різноманітних завад, неточністю зчитування показів приладів, округленням під час приведення даних до однакових умов обробки інформації — список умов виникнення похибок можна продовжити, але для обґрунтування МНК цього досить.

Тож через наявність цих похибок в експериментальних значеннях x₁, x₂, y₁, y₂ безпосередній розв’язок системи рівнянь (3.34) відносно a та b може нести в собі похибку в 10, 100, 1000 і більше відсотків.

Наприклад, якщо використати лише значення (рис. 3.1) для розв’язання системи рівнянь (3.34), то похибка буде вже не у відсотках, а у характері функціональної залежності (пунктирна лінія на рис. 3.1).

У свій час Гаусс запропонував інший спосіб визначення коефіцієнтів a, b моделі (3.33). Він запропонував сформувати суму квадратів різниць ∑^N між теоретично заданими за допомогою рівняння (3.33) значеннями вихідної координати y при значеннях аргументу x_i, i = 1,N та її експериментальними значеннями y_i:

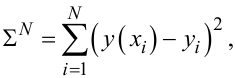(3.35)

а потім знайти такі значення коефіцієнтів a , b рівняння (3.33), котрі мінімізують вираз (3.35).

Від цієї процедури і назва методу — метод найменших квадратів.

З курсу математичного аналізу відомо, що для знаходження мінімуму якоїсь функції необхідно взяти від неї похідну, прирівняти цю похідну до нуля і розв’язати отримане рівняння — його корінь задає значення аргументу, за якого функція досягає мінімуму, а само значення функції у цій точці, якщо вона опукла донизу, задає її мінімальне значення.

Згідно з цією ідеєю, підставимо у вираз (3.35) замість y(x_i) його значення з (3.33) і візьмемо від отриманого виразу частинні похідні за b та a, які прирівняємо до нуля, тобто

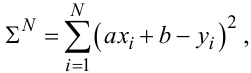(3.36)

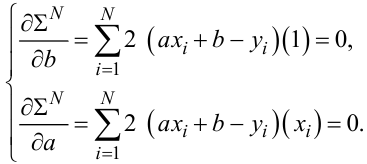(3.37)

Із (3.37) після низки нескладних перетворень отримаємо:

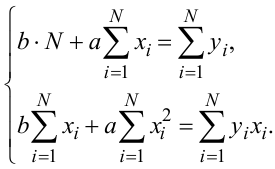(3.38)

Розв’язавши систему рівнянь (3.38) відносно b і a , отримаємо такі їх значення, які мінімізують суму квадратів відхилень експериментально виміряних значень величин x_i, y_i від теоретично заданих згідно з вибраною функціональною залежністю.

Рівняння, що входять у систему (3.38), називають нормальними рівняннями Гаусса. Коефіцієнтами у них є суми, які «згладжують» дію похибок вимірювань величин x, y і зменшують їх вплив на оцінки параметрів b, a. Завдяки цьому підвищується точність їх визначення.

А тепер припустимо, що поле точок (x_i, y_i) експериментально визначених величин x , y має такий вигляд, як це показано на рис. 3.2.

Із цього рисунка видно, що середньою лінією цього поля, яка віддзеркалює «в середньому» функціональну залежність y від x , є парабола

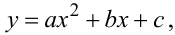(3.39)

параметри якої a, b, c також доцільно визначати за допомогою МНК.

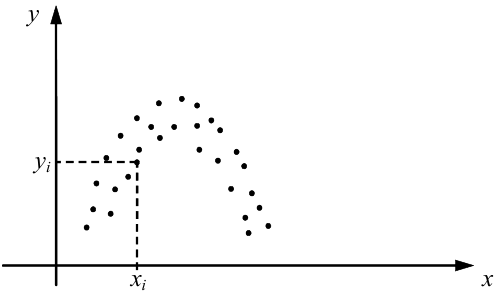
Рисунок 3.2 — Поле точок (x_i, y_i) експериментально визначених величин x, y

Для отримання нормальних рівнянь Гаусса у цьому випадку підставимо (3.39) у (3.35), що дасть вираз

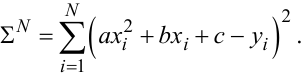(3.40)

Далі від цього виразу візьмемо частинні похідні за c , b, a та прирівняємо їх нулю, що дасть систему рівнянь:

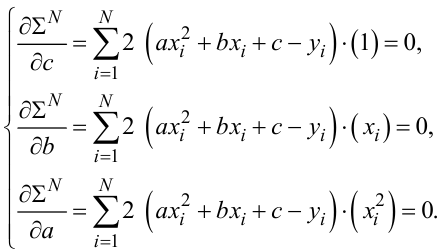(3.41)

Після спрощень в системі (3.41) матимемо систему нормальних рівнянь Гаусса (3.42), розв’язавши яку отримаємо оптимальні за критерієм мінімуму відхилень експерименту від теорії значення параметрів c, b, a математичної моделі (3.39) функціональної залежності величини y від величини x, заданих експериментальним полем точок (x_i, y_i), яке зображено на рис. 3.2:

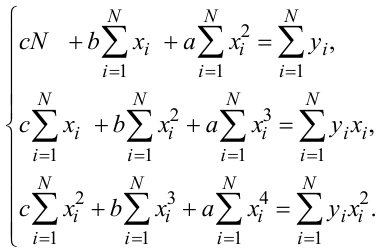(3.42)

Приклад. Нехай в результаті експерименту отримана послідовність десяти парних значень величин x, y, яка наведена у табл. 3.1.

Таблиця 3.1 — Експериментальні дані та проміжні дані їх обробки

i	1	2	3	4	5	6	7	8	9	10
xi	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8	2,0
yi	1,16	1,30	1,20	1,20	0,6	0,6	0,4	0	-0,5	-1,0
xi2	0,04	0,16	0,36	0,64	1,0	1,44	1,96	2,56	3,24	4,0

Якщо нанести на координатну площину x , y ці точки, то можна побачити, що це є «збурена» завадами парабола. Але спочатку спробуємо використати для побудови моделі цієї залежності рівняння прямої (3.33).

Підставляючи значення x_i, y_i, i = 1,10 із табл. 3.1 у рівняння (3.38), отримуємо:

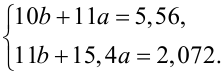(3.43)

Розв’язком системи рівнянь (3.43) є оцінки

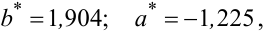(3.44)

які задають модель залежності у вигляді прямої лінії

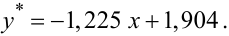(3.45)

А тепер використаємо для побудови моделі залежності, заданої табл. 3.1, рівняння параболи (3.39).

Підставляючи значення x_i, y_i, i = 1,10 із табл. 3.1 у рівняння (3.42), отримуємо:

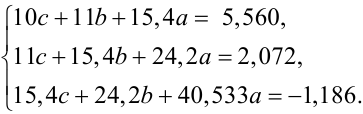(3.46)

Розв’язком системи рівнянь (3.46) є оцінки

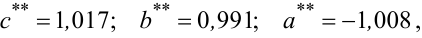(3.47)

які задають модель вказаної вище залежності у вигляді параболи

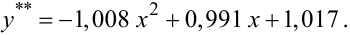(3.48)

Для того, щоб визначити яка із двох моделей (3.45), (3.48) краще віддзеркалює функціональну залежність, що задана табл. 3.1, знайдемо числове значення критеріальних співвідношень (3.36), (3.40) з використанням (3.44) та (3.47).

Із (3.36) та (3.44) для поля точок, заданих табл. 3.1, знаходимо, що

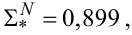(3.49)

а із (3.40) та (3.47), що

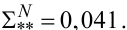(3.50)

Отже, оскільки

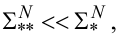(3.51)

то, згідно з основною ідеєю МНК, модель (3.48) є набагато кращою, ніж модель (3.45), у чому легко переконатись, якщо нанести поле точок із табл. 3.1 на координатну площину (x, y) (рис. 3.3).

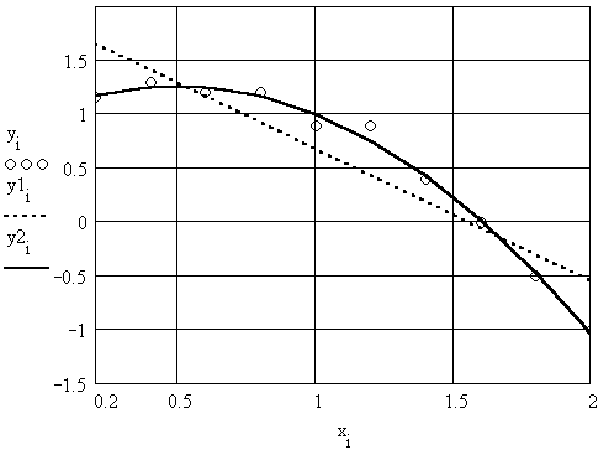
Рисунок 3.3 — Поля точок (x_i, y_i), (x_i, y1_i) і (x_i, y2_i) експериментально визначених величин x, y та величин y1 і y2, обчислених у ППП MathCAD за методом найменших квадратів і яким відповідають у тексті величини y* та y^** (точки графіка залежності y(x) нанесені у вигляді маленьких кіл; графік функції y1(x) зображений у вигляді пунктирної лінії, а графік функції y2(x) — у вигляді суцільної)

З усього викладеного у даному підрозділі можна зробити такі висновки:

1) за вибраної структури моделі функціональної залежності оптимальні значення її параметрів у межах заданого діапазону значень аргументу та його функції найбільш просто і ефективно визначаються за допомогою МНК;

2) вибір виду та структури моделі є прерогативою дослідника;

3) у класі заданих структур МНК дозволяє отримати не лише оптимальні значення коефіцієнтів, але й оптимальну структуру моделі.

На завершення цього підрозділу зробимо одне надзвичайно важливе зауваження, а точніше, попередження, яке полягає у тому, що, оскільки обчислювальні алгоритми МНК побудовані виключно на основі апроксимаційних процедур, то їх використання для розв’язання задач екстраполяції може призвести до неприпустимих помилок. Іншими словами, за допомогою МНК можна успішно розв’язувати задачі оптимізації відновлювання сигналів на вході вимірювальної системи за інформацією про її вихід та задачі оптимального синтезу динамічної характеристики (наприклад, передаточної функції) системи, за інформацією про її вхід та вихід, але ні в якому разі за допомогою МНК не можна синтезувати моделі прогнозу.

Про те, яких значень можуть сягати помилки через ігнорування цього попередження, легко зробити висновок із рис. 3.4.

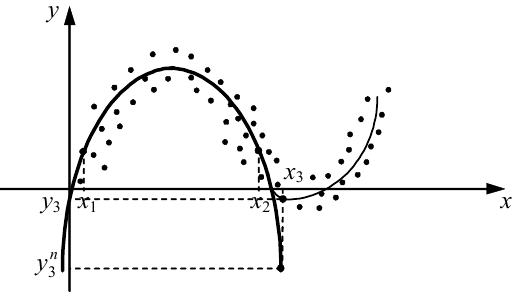
Рисунок 3.4 — Графічна ілюстрація недоцільності використання МНК для розв’язання задачі прогнозування

З рис. 3.4 видно, що якщо маємо лише точки з діапазону значень координати x від x₁ до x₂, то МНК як оптимальну модель залежності y = f(x) дасть параболу. Під час використання цієї параболи для прогнозування значення y у точці x₃ отримаємо значення y₃ⁿ, у той же час як реально координата y матиме значення y₃, яке суттєво відрізняється від y₃ⁿ.

На жаль, сьогодні навіть у дисертаціях та монографіях можна зустріти приклади використання МНК під час синтезу моделей прогнозу.

Ми сподіваємось, що всі, хто користуватиметься цим посібником, такої помилки припускатись не будуть.