4.1 Основні характеристики стаціонарних випадкових процесів

Строга математична модель безперервного випадкового процесу припускає, що він протікає у часі від мінус нескінченності до плюс нескінченності, тобто t ∈(-∞, ∞). А ту його частину x^*(t), яку вдалося у якийсь спосіб зафіксувати, називають реалізацією випадкового процесу x(t).

Для будь-якої реалізації x^*(t) безперервного випадкового процесу x(t) характерним є те, що вона містить у собі нескінченну кількість щільно розміщених поряд у часі значень x(t) на будь-якому скінченному відрізку часу [t_n,t_к], обмеженому моментами початку t_n та кінця t_к реєстрації, тобто для em>x^*(t) справедливим є те, що t∈[t_n,t_к].

Зрозуміло, що якщо випадковий процес є дискретним у часі x(t_i), то його реалізація x^*(t_iM/) є скінченною послідовністю випадкових чисел x_i, i = 1,N, зафіксованих на відрізку часу [t_n,t_к], що можна віддзеркалити у такий спосіб:

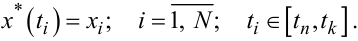(4.1)

У зв’язку з накладенням людьми на безперервний плин часу t циклічної системи його відліку (секунда, хвилина, доба, рік), що пов’язано із циклічністю обертання Землі навколо Сонця, зручно початок t кожної реалізації x^*(t) відносити до початку відповідного циклу відліку часу. Це дає змогу, накладаючи реалізації на їх графіку одна на одну, вивчати їх у сукупності, оскільки лише за такого підходу вдається встановити певні закономірності випадкових процесів і визначити цілий ряд цікавих їх числових і функціональних характеристик.

Як приклад на рис. 4.1 показані три добові реалізації споживання електричної потужності P_ел містом, наближеним за розмірами та промисловими характеристиками до середнього для України.

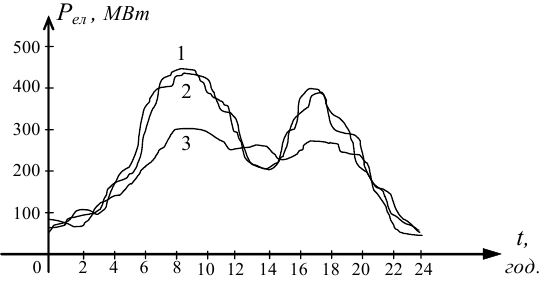
Рисунок 4.1 — Графік трьох добових реалізацій процесу споживання електричної потужності містом, середніх для України розмірів

Перша та друга реалізації характеризують добове споживання електричної потужності у середині тижня, а третя — у вихідний день, коли більшість підприємств не працюють, а побутові витрати стають більшими навіть у години обідньої перерви.

Для подальших викладок потрібні будуть деякі елементарні положення із теорії ймовірностей — нагадаємо їх

Однією з основних характеристик випадкової величини X є її функція розподілу F(x), яка задає ймовірність P(X ≤ x) отримання випадковою ве- личиною X конкретного значення, не більшого від значення x, тобто

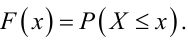(4.2)

Графік функції розподілу F(x) безперервної випадкової величини X має вигляд, наведений на рис. 4.2.

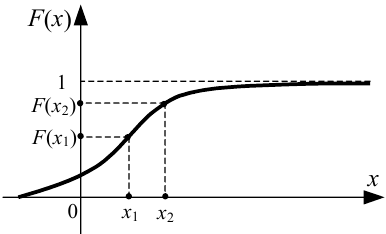
Рисунок 4.2 — Графік функції F(x) розподілу безперервної випадкової величини X

Нагадаємо властивості функції F(x) розподілу безперервної випадкової величини X:

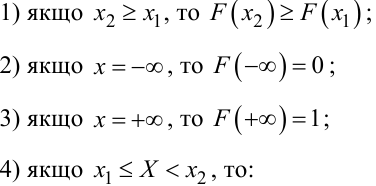
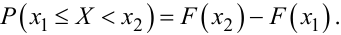(4.3)

Перша із цих властивостей означає, що графік функції розподілу безперервної випадкової величини X є безперервною зростаючою зі зростанням аргументу x кривою.

Друга властивість означає, що випадкова величина X не може мати значень, менших від мінус нескінченності.

Третя властивість означає, що випадкова величина X не може мати значень, більших від плюс нескінченності.

А четверта властивість означає, що для знаходження ймовірності потрапляння випадкової величини X у проміжок значень [x₁, x₂) достатньо взяти різницю значень її функції розподілу F(x) на границях цього проміжку.

Всі ці властивості є справедливими і для дискретної випадкової величини, але слід пам’ятати, що графік її функції розподілу має східчасту форму (рис. 4.3)

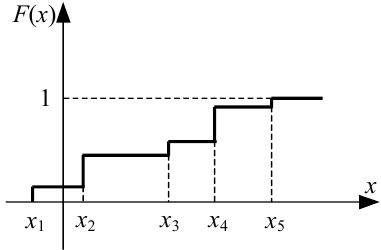
Рисунок 4.3 — Графік функції F(x) розподілу дискретної випадкової величини X за умови, що величина X здатна набувати лише одне із п’яти значень x₁, x₂, x₃, x₄, x₅

Похідна від функції розподілу F(x) безперервної випадкової величини X задає густину f(x) ймовірностей значень цієї величини, тобто

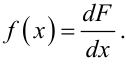(4.4)

Нагадаємо властивості густини f(x) ймовірностей безперервної випадкової величини X:

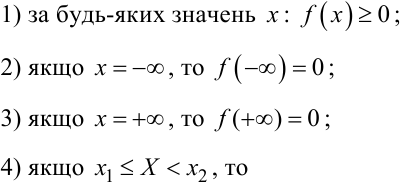
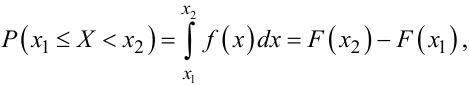(4.5)

причому:

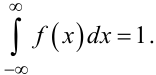(4.6)

Інтерпретація перших трьох властивостей густини імовірностей P(x) безперервної випадкової величини X така ж, як і та, що була дана для перших трьох властивостей її функції розподілу f(x), а четверта властивість вказує на те, що імовірність потрапляння випадкової величини X у проміжок значень [x₁, x₂) чисельно дорівнює площі фігури під кривою f(x), відсіченої ординатами при x = x₁ та x = x₂. П’ята властивість є наслідком попередніх відносно f(x) та F(x).

Здійснюючи графічне диференціювання кривої F(x), зображеної на рис. 4.2, неважко переконатись у тому, що графік густини імовірностей f(x) має вигляд, наведений на рис. 4.4. В інших випадках графік функції f(x) може бути дещо іншим — він може бути зсунутим вліво чи вправо, але незмінними є дві обставини. По-перше, для всіх значень x повинна виконуватись нерівність f(x) ≥ 0, а по-друге, площа під кривою ff(x) завжди повинна дорівнювати одиниці.

Зазначимо, що для дискретної випадкової величини поняття густини ймовірностей не існує, оскільки похідна від її функції розподілу має розриви 2-го роду на початку кожної сходинки, що робить її принципово невизначеною.

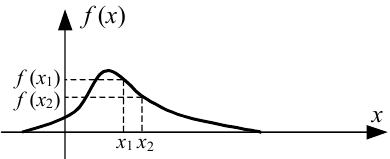
Рисунок 4.4 — Графік густини імовірностей f(x) безперервної випадкової величини X, отриманий графічним диференціюванням кривої F(x), зображеної на рис. 4.2

Однак для аналізу дискретних випадкових процесів поняття густини і не потрібне.

Дуже важливими характеристиками як безперервної, так і дискретної випадкової величини X є її математичне очікування m_x та дисперсія D_x або позитивне значення кореня квадратного з неї, яке називають середньоквадратичним відхиленням σ_x. Перша з цих характеристик — mx — задає теоретичне середнє значення випадкової величини X, а друга — D_x чи σ_x — характеризує розкид значень випадкової величини X відносно її середнього значення m_x.

Для неперервної випадкової величини X:

(4.7)

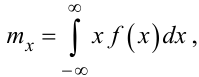(4.8)

а для дискретної:

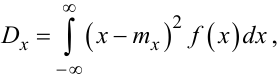(4.9)

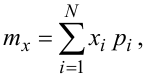(4.10)

де p_i — імовірність того, що дискретна випадкова величина X набуде значення x_i:

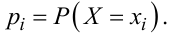(4.11)

Звертаємо увагу на те, що у термінах теоретичної механіки формула (4.7) задає перший початковий момент, а формула (4.8) — другий центральний момент густини розподілу f(x) безперервної випадкової величини X. А тому математичне очікування mx випадкової величини X, незалежно від того, є вона неперервною чи дискретною, часто називають першим початковим моментом цієї випадкової величини, не пов’язуючи це з тим, визначена чи ні для неї густина ймовірностей. За аналогією D_x називають другим центральним моментом випадкової величини X.

Узагальнюючи, можна зазначити, що j-ий початковий момент m_j(x) випадкової величини X можна визначити як математичне очікування j-го ступеня цієї величини, тобто

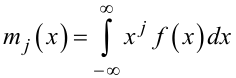(4.12)

для безперервного випадку, або

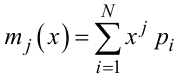(4.13)

для дискретного.

За аналогією j-ий центральний момент випадкової величини X можна визначити як математичне очікування j-го ступеня відхилення цієї величини від її середнього значення, тобто

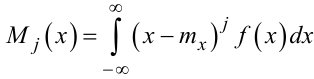(4.14)

для безперервного випадку, або

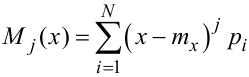(4.15)

для дискретного.

Очевидно, що

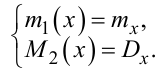(4.16)

Очевидно й те, що

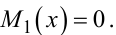(4.17)

Для кого тотожність (4.17) не очевидна, доведіть її справедливість самостійно, скориставшись формулами (4.14), (4.7) та (4.6).

Нагадавши вищевикладені елементи теорії ймовірностей відносно випадкових величин X, повернемося знову до випадкових процесів X(t), які є теж випадковими величинами, але прив’язаними до плину часу.

Якщо розглядати час як параметр, який можна «зупинити», зафіксувавши на конкретному значенні t^*, то будь-яку сукупність реалізацій x^*(t) випадкового процесу X(t) можна «порізати» прямими, паралельними осі X, встановивши перпендикуляри із кожного значення t^*.

Випадкову величину X(t^*), яка формується в кожному «перерізі» t^* сукупністю реалізацій x^*(t) випадкового процесу X(t), можна характеризувати густиною ймовірностей f(x,t^*), а для всього процесу можна, «відпустивши» t^*, сформувати густину імовірностей f(x,t), в якій, нагадаємо, t є безперервним параметром із детерміновано визначеними нами, чи кимось іншим, значеннями.

Очевидно, що формули (4.7), (4.8) для безперервного випадкового процесу X(t) перетворюються на:

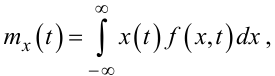(4.18)

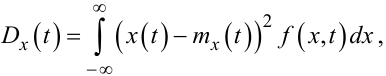(4.19)

а математичне очікування m_x(t) та дисперсія D_x(t) у загальному випадку стають функціями часу t, як це видно на рис. 4.1, з якого легко бачити, що середні значення електричної потужності P_ел, яка споживається містом у 2 години ночі і у 9 годин ранку, суттєво відрізняються; як суттєво відрізняється і розкид відхилення цієї потужності у ці ж години від її середнього значення.

Тепер уявимо собі, що дві реалізації x^*(t) деякого випадкового процесу X(t) мають вигляд, наведений на рис. 4.5.

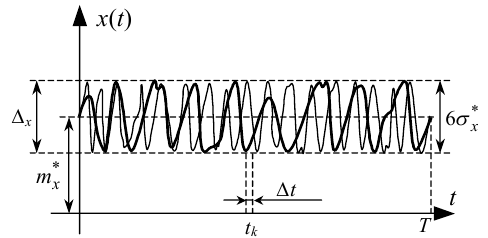
Рисунок 4.5 — Графік двох реалізацій деякого випадкового процесу X(t)

Навіть «неозброєним» оком видно, що і середнє значення цього процесу, і його дисперсія є не функціями часу, а константами, тобто

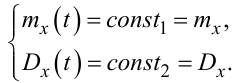(4.20)

Однак, згідно з формулами (4.18), (4.19), такий результат можна отримати лише в одному випадку, коли

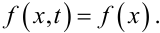(4.21)

А це, у свою чергу, справедливо лише для безперервного випадкового процесу X(t), густина ймовірностей у кожному «перерізі» t сукупності реалізацій x^*(t) якого описується одним і тим же законом f(x), тобто не залежить від t.

Випадкові процеси, для яких виконується умова (4.21) і, як наслідок, умова (4.20), відносять до класу стаціонарних випадкових процесів.

Відзначимо, що математики розрізняють стаціонарність у широкому та у вузькому розумінні, пов’язуючи це з багатовимірними функціями розподілу випадкових процесів, що їх відносять до моделей красивих, але практично не придатних для розв’язання конкретних задач. В інженерних задачах стаціонарність випадкових процесів і у широкому, і у вузькому розумінні збігається, а тому не будемо ускладнювати матеріал введенням багатовимірних функцій розподілу цих процесів.

У класі стаціонарних випадкових процесів X(t) виділяють підклас ергодичних, для яких усереднення на множині значень x дає той же результат, що й усереднення в часі t.

Це означає, що математичне очікування mx та дисперсію D_x ергодичного випадкового процесу X(t) можна отримати не лише за допомогою формул (4.18), (4.19), але і за допомогою формул, набагато простіших за структурою обчислень:

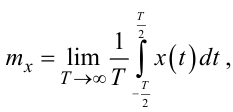(4.22)

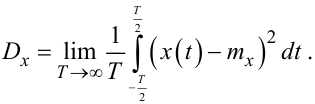(4.23)

Одразу ж зазначимо, що всі стаціонарні випадкові процеси, з якими під час розв’язання практичних професійних задач мають справу інженери, є ергодичними, а тому формули (4.22), (4.23) для обчислення очікуваного середнього значення процесу m_x та характеристики його відхилень від середнього значення - очікуваної дисперсії D_x — є основними у теоретичному плані.

Але у практиці розрахунків використовуються дещо інші формули:

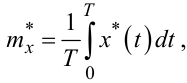(4.24)

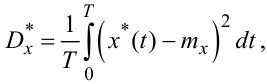(4.25)

за якими знаходяться статистична оцінка m_x^* математичного очікування m_x ергодичного випадкового процесу X(t) та статистична оцінка D_x^* дисперсії D_x цього процесу з використанням однієї, але достатньо інформативної реалізації x^*(t) випадкового процесу X(t), зафіксованої на відрізку часу T.

Очевидно, що оцінки m_x^* та D_x^* теж є випадковими величинами, залежними від довжини T реалізації x^*(t), але, зрозуміло, що дисперсія цих оцінок є набагато меншою у порівнянні із дисперсією процесу X(t) і з ростом T наближається до нуля.

Нагадаємо, що до статистичних оцінок числових характеристик випадкових величин математична статистика висуває три вимоги: по-перше, вони повинні бути незміщеними, по-друге, ефективними, а по-третє, переконливими.

Вимога незміщеності означає, що з ростом T рано чи пізно значення оцінки точно збіжиться зі значенням відповідної числової характеристики.

Вимога ефективності означає, що із множини різноманітних формул, які можуть бути запропоновані для отримання числового значення оцінки, необхідно вибирати ту, за допомогою якої оцінка визначається з найменшою власною дисперсією.

Вимога переконливості (російською мовою — «состоятельности») означає, що оцінка з ростом T повинна безперервно наближатись до числової характеристики, що дає право зупиняти обчислення варіантів оцінки, як тільки вони перестають відрізнятись один від одного у заданих межах.

Більш детально ознайомитись із вимогами до статистичних оцінок числових характеристик випадкових величин можна у будь-якому з посібників із теорії ймовірностей та математичної статистики. А у нашому посібнику згадаємо ще лише про те, що мало знайти числове значення статистичної оцінки m_x^* чи D_x^*. Треба обов’язково це значення доповнити визначенням довірчого інтервалу, в який із деякою наперед заданою довірчою імовірністю потрапляє отримане значення статистичної оцінки. Оскільки, ще раз підкреслимо, статистичні оцінки є теж випадковими величинами, то дуже важливо знати, за які межі вони не вийдуть, якщо нарощувати масиви інформації, що використовуються у розрахунках.

За тим, як розраховуються довірчі інтервали для оцінок числових характеристик випадкових величин, відсилаємо до навчальних посібників з математичної статистики.

Декілька корисних порад

Порада перша. Якщо, зафіксувавши реалізацію безперервного випадкового процесу x(t), ви бачите (див. рис. 4.5), що вона не виходить за межі деякої смуги, границі якої проходять паралельно осі часу, і досить часто наближається до обох границь, то можете не сумніватись у тому, що процес X(t) є не лише стаціонарним, але й ергодичним.

Порада друга. Для грубої оцінки середнього значення m_x^* ергодичного процесу X(t) за зафіксованою на відрізку часу T його реалізацією x(t) досить «на око» провести паралельно осі t вісь «квазісиметрії» цієї реалізації (див. рис. 4.5), відстань від якої до осі t і дасть значення оцінки m_x^* з похибкою не більше 5%.

Порада третя. Для грубої оцінки середньоквадратичного відхилення 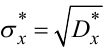процесу X(t) від середнього значення m_x необхідно ширину смуги Δ_x, за межі якої не виходить реалізація x(t) за умови, що лінія m_x^* проходить центром смуги, розділити на шість, тобто

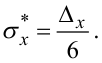(4.26)

Формула (4.26) є наслідком відомого у математичній статистиці «правила трьох сигм», згідно з яким всі значення нормально розподіленої величини X з імовірністю 0,997 знаходяться у смузі значень

Нагадаємо, що нормально розподіленою (гауссівською) називається така випадкова величина, густина ймовірностей якої задається законом:

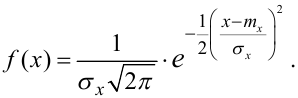(4.27)

Порада четверта. Якщо для подальших розрахунків потрібне якомога точніше значення оцінки m_x^*, то, вибравши по можливості якомога менший інтервал квантування часу Δ_t (див. рис. 4.5), сформуйте з реалізації x(t) решітчасту функцію x(k · t Δ_t) = x_k, середнє значення якої знаходиться за допомогою виразу, що є дискретним аналогом (4.24), а саме:

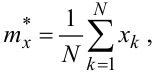(4.28)

де 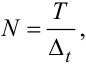, або

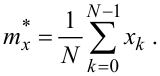(4.29)

Оцінка m_x^* за допомогою формули (4.28) чи (4.29) є незміщеною, ефективною і переконливою.

Порада п’ята. Під час використання решітчастого аналога x_k ергодичного випадкового процесу X(t) для обчислення оцінки дисперсії за дискретним аналогом формула (4.25) набуває вигляду:

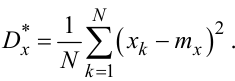(4.30)

Оскільки в формулі (4.30) доводиться використовувати не математичне очікування m_x випадкового процесу X(t), а його статистичну оцінку m_x^*, знайдену за формулою (4.27) чи (4.28), то оцінка дисперсії буде незміщеною, ефективною і переконливою лише тоді, коли вона знаходиться за формулою:

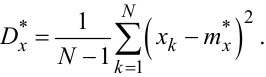(4.31)

Звичайно, якщо число N є значним, то формули (4.30) та (4.31), у разі використання в обох m_x^*, будуть давати практично один і той же результат, але вже при N = 20 результати різнитимуться на 5%, а з подальшим зменшенням N ця різниця зростатиме