4.2 Кореляційні функції та спектральні густини стаціонарних випадкових процесів

Нехай маємо сукупність добових реалізацій такого випадкового процесу, як зміна температури зони обмотки статора електричного двигуна конвеєра, яка є функцією струму, що протікає у цій обмотці. Випадковість значень цього процесу залежить від рівномірності подачі та гранулометричного складу того сипучого чи кускового матеріалу, який транспортується цим конвеєром.

Якщо струм зростає, то і температура зони теж зростає. Якщо струм спадає, то з деяким запізненням спадає і температура зони. Очевидно, що від значення температури у зоні в даний момент часу суттєво залежить те її значення, якого вона набуде через одну хвилину. Через 10 хвилин ця залежність уже буде менш помітною. Ще меншим температурний вплив буде через 100 хвилин. А через 1000 хвилин навряд чи є сенс його взагалі оцінювати.

Оскільки, як було зазначено, температурний процес, що розглядається, є випадковим, то безпосередньо оцінити вплив одного його значення на інше неможливо.

Для оцінювання лінійного зв’язку між двома значеннями x₁, x₂ випадкового процесу X(t) у момент часу t₁ та t₂ математики ввели таку характеристику, як кореляційна функція K_x(t₁, t₂), яку визначають як

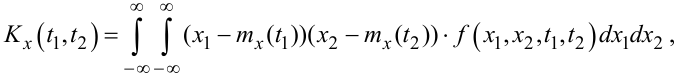(4.32)

де f(x₁,x₂,t₁,t₂) — двовимірна густина ймовірностей випадкового процесу X(t), котра визначається у моменти часу t₁,t₂, відносно яких випадковий процес X(t) можна розглядати як систему двох випадкових величин X₁ та X₂, значеннями x₁ та x₂ яких є значення x(t₁), x(t₂) реалізацій випадкового процесу, зафіксовані у моменти часу t₁, t₂ :

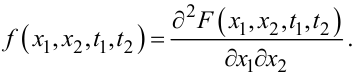(4.33)

F(x₁,x₂,t₁,t₂) — двовимірна функція розподілу ймовірностей випадкового процесу X(t), яка задає значення ймовірності того, що у момент t₁ викону- ється нерівність X₁ ≤ x₁, а у момент t₂ виконується нерівність X₂ ≤ x₂, тобто

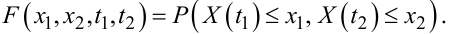(4.34)

Слід зазначити, що формула (4.32) грає не стільки практичну, скільки загальнотеоретичну роль, оскільки на практиці ніхто не проводить оцінювання функцій f(x₁,x₂,t₁,t₂) та FF(x₁,x₂,t₁,t₂) за експериментальними даними.

Формула (4.32) навіть у теоретичному плані спрощується для стаціонарного випадкового процесу X(t), для якого двовимірна густина f(•) та функція розподілу F(•) ймовірностей залежать не від конкретних значень t₁, t₂ моментів часу t, а лише від їх різниці τ = t₁ - t₂, тобто

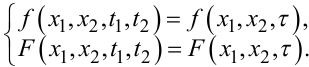(4.35)

З урахуванням (4.35), формула для кореляційної функції стаціонарного випадкового процесу X(t) набуває вигляду:

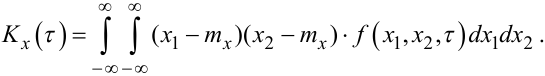(4.36)

Але і формулу (4.36) у практичних розрахунках теж не використовують, оскільки оцінку двовимірної густини ймовірностей f(x₁,x₂,τ) за експериментальними даними визначати непросто. Набагато простішим є визначення кореляційної функції K_x(τ) стаціонарного випадкового процесу X(t) з використанням властивості ергодичності, згідно з якою оцінка кореляційної функції K_x^*(τ) може бути визначена як

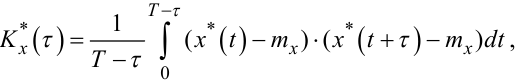(4.37)

де T — відрізок часу, протягом якого фіксується реалізація x^*(t) випадкового процесу X(t).

Математиками доведено, що для ергодичного випадкового процесу

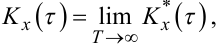(4.38)

що дає право за оцінку K_x^*(τ) кореляційної функції K_x(τ) брати будь-яку функцію, отриману за допомогою формули (4.37).

Очевидно, що чим більшим є значення T, тим точніше оцінка K_x^*(τ) відображає кореляційну функцію K_x(τ).

Аналізуючи формулу (4.37), бачимо, що для отримання значення оцінки K_x^*(τ) кореляційної функції K_x(τ) ергодичного випадкового процесу X(t) для значення τ₁ параметра τ при реалізації X^*(t) цього процесу (рис. 4.6, а) необхідно, зсунувши цю реалізацію на відрізок часу t = τ₁ (рис. 4.6, б), перемножити одна на одну на відрізку [0,T - τ₁] основну та

«зсунуту» реалізації X^*(t), знайти площу під кривою, яка є результатом цього перемноження, і поділити отриману площу на довжину відрізка інтегрування T - τ₁.

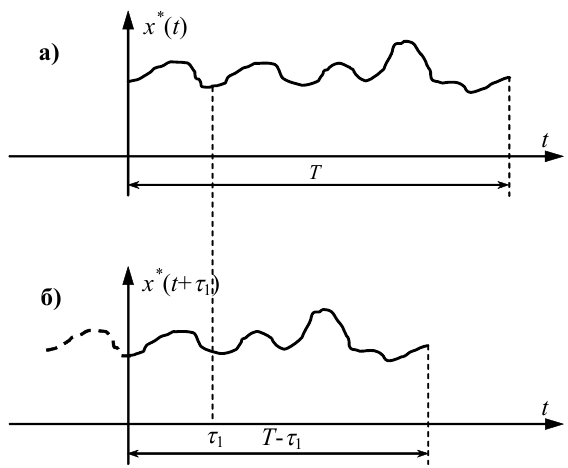
Рисунок 4.6 — Геометрична інтерпретація формування підінтегрального виразу у формулі (4.37)

Зрозуміло, що з ростом τ точність визначення значень K_x(τ) зменшується, оскільки зменшується інтервал «перекриття» основної та «зсунутої» на відрізок τ реалізації x^*(t), що у разі використання чисельних методів приводить до зменшення кількості значень випадкового процесу X(t), які беруть участь у формуванні підінтегрального виразу у формулі (4.37).

Оскільки результати інтегрування у формулі (4.37) не залежать від того, вправо чи вліво на τ «зсувається» реалізація x^*(t), то справедливим є вираз

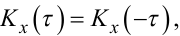(4.39)

який констатує той факт, що кореляційна функція випадкового процесу є симетричною відносно осі ординат.

Підставивши у формулу (4.37) τ = 0, отримаємо:

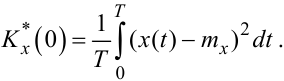(4.40)

Порівнюючи вираз (4.40) з виразом (4.25), бачимо, що вони дають один і той же результат, тобто

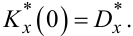(4.41)

Результатові (4.41) можна дати таку інтерпретацію — значення K_x(0) кореляційної функції K_x(τ) центрованого ергодичного випадкового процесу X(t) за нульового зсуву τ = 0 дорівнює дисперсії D_x або, що одне і те ж, σ_x². Нагадаємо, що центрованим називається довільний випадковий процес X(t), від усіх значень x(t) якого віднімається його середнє значення m_x(t) на ковзному інтервалі (рис. 4.7).

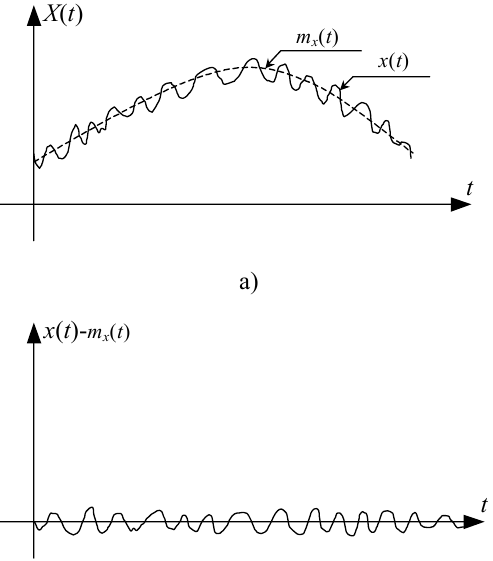
Рисунок 4.7 — Графічна інтерпретація центрування випадкового процесу

З рис. 4.7 видно, що навіть нестаціонарний випадковий процес (рис. 4.7, а) у разі його центрування може стати не лише стаціонарним (рис. 4.7, б), але й ергодичним.

Зазначимо, що, як правило, під час розв’язання практичних інженерних задач, оцінки кореляційних функцій визначаються саме для центрованих випадкових процесів, для яких у такому випадку майже завжди присутня ергодичність.

При виконанні практичного аналізу центрованих ергодичних випадкових процесів, які мають місце при розв’язанні інженерних задач, найбільше розповсюдження отримали чотири моделі кореляційних функцій цих процесів, а саме:

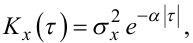(4.42)

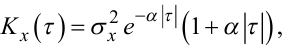(4.43)

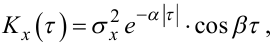(4.44)

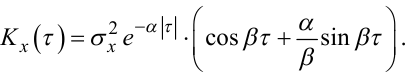(4.45)

Приклади графіків кореляційних функцій, заданих моделями (4.42) та (4.44), показані на рис. 4.8.

Зазначимо, що моделі (4.43) та (4.45) можна інтерпретувати як «розтягувальні» по осі τ для моделей (4.42) та (4.44).

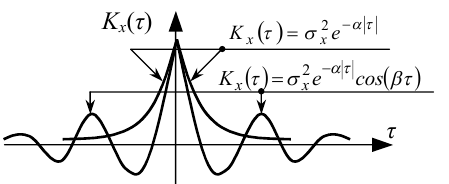
Рисунок 4.8 — Приклади графіків кореляційних функцій ергодичних випадкових процесів

А тепер розглянемо такий специфічний технологічний об’єкт, як кульовий млин, який використовується для тонкого помолу залізної руди перед подальшим збагаченням її у флотаційній машині.

Кульовим млином є циліндр, на третину заповнений металевими кулями, який має вхідний отвір для подачі подрібненої залізної руди та вихідний отвір для відбору тієї ж залізної руди, але перетертої на пил металевими кулями під час їх хаотичного переміщення разом із залізною рудою внаслідок обертання циліндра навколо повздовжньої осі за допомогою потужного електропривода.

Очевидно, що зміна в часі і гранулометричного складу X(t) подрібненої залізної руди на вході млина, і струму якоря його приводного електродвигуна Y(t) є випадковими процесами, які в усталеному режимі роботи млина можна вважати не лише стаціонарними, а й ергодичними.

Очевидним є і те, що лише середнє значення струму Y(t) функціонально залежить від середнього значення гранулометричного складу X(t), а кожне конкретне значення процесу Y(t) функціонально зв’язати з конкретними значеннями процесу X(t) не можна, оскільки на випадковість значень Y(t) суттєво впливає не лише процес X(t), але і внутрішній процес постійних змін самої структури кульового млина, викликаний як переміщенням металевих куль одна відносно одної та стінок циліндричного барабана, так і переміщенням шматочків руди між кулями та між собою.

Тож для характеристики усередненого лінійного зв’язку між значеннями випадкового процесу X(t) у часовому перерізі t₁ та випадкового процесу Y(t) у часовому перерізі t₂ (рис. 4.9) математики вводять таку характеристику, як взаємна кореляційна функція K_yx(t₁,t₂), для якої справедливим є вираз

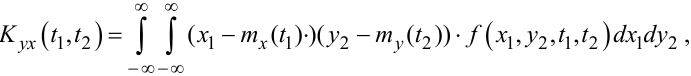(4.46)

де

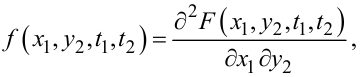(4.47)

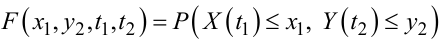(4.48)

відповідно, двовимірні взаємні густина f(•) та функція розподілу F(•) ймовірностей процесів X(t) та YY(t).

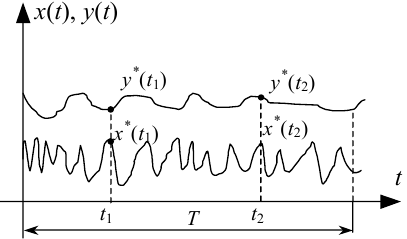
Рисунок 4.9 — Графіки реалізацій x^*(t), y^*(t) взаємопов’язаних випадкових процесів X(t), Y(t), зафіксованих на проміжку часу T

Для стаціонарних випадкових процесів X(t) та Y(t) за аналогією з (4.34) — (4.36) маємо:

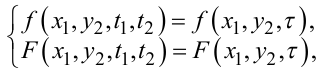(4.49)

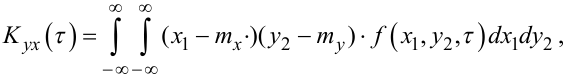(4.50)

а для ергодичних випадкових процесів за аналогією з (4.37), (4.38):

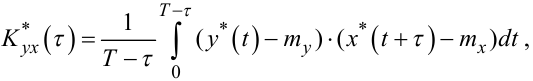(4.51)

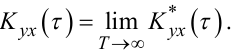(4.52)

Приклади графіків можливих взаємних кореляційних функцій центро- ваних ергодичних процесів X(t), Y(t) наведені на рис. 4.10.

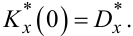
Рисунок 4.10 — Приклади графіків взаємних кореляційних функцій центрованих ергодичних процесі

Зсув максимуму взаємної кореляційної функції K_yx(τ) на відрізок τ^* вправо від осі ординат характеризує той відрізок часу, на який запізнюється поява на виході системи процесу Y(t) відносно процесу X(t), котрий його викликав, оскільки значення реакції системи найкраще корелюється саме з тим значенням вхідного процесу, яке його викликало.

Тобто τ^* можна використовувати як одну з характеристик інерційних властивостей системи, що продукує процес Y(t) у відповідь на вхідний для неї процес X(t). Якщо застосувати до кореляційної функції K_x(τ) перетворення Фур’є, тобто взяти інтеграл

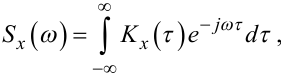(4.53)

тоді отримаємо іншу характеристику стаціонарного випадкового процесу, яку називають його спектральною густиною S_x(ω), оскільки вона характеризує щільність спектра частот гармонічних складових з випадковими значеннями амплітуди і фази, сукупністю яких можна задати даний процес.

Для прикладу отримаємо спектральну густину стаціонарного випадкового процесу X(t), який має кореляційну функцію (4.42).

Підставивши (4.42) у (4.53), отримаємо

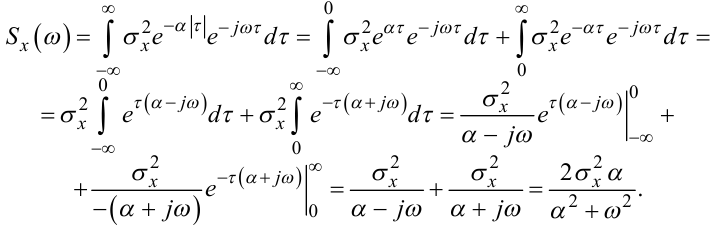(4.54)

Аналізуючи вирази (4.42) та (4.54) разом, бачимо, що чим більшим є значення α, тим швидше «згасає» кореляційна функція K_x(ω) і тим повільніше «згасає» спектральна густина S_x(ω), тобто чим менше значень випадкового процесу X(t) корелюються між собою, тим більше необхідно гармонічних складових для адекватного представлення цього процесу у частотній області. На рис. 4.11 показані два графіки кореляційних функцій K_x(ω) при σ_x² = 1 та α = 1 і α = 2 (рис. 4.11, а), а також два графіки спектральних густин S_x(ω) для цих же значень σ_x² і ω (рис. 4.11, б).

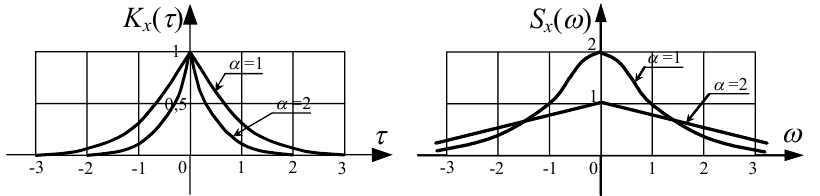
Рисунок 4.11 — Приклади графіків кореляційних функцій K_x(τ) стаціонарних випадкових процесів та їх спектральних густин S_x(ω)

Очевидно, що, перетворюючи за Фур’є взаємну кореляційну функцію K_xy(ω) стаціонарних випадкових процесів X(t) та Y(t), отримаємо взаємну спектральну густину S_yx(jω) цих процесів, тобто

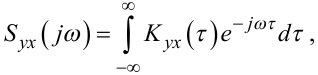(4.55)

яка, на жаль, вже буде комплексною функцією, оскільки підінтегральна функція у (4.55) K_yx(τ) не є симетричною відносно осі ординат.

Особливу роль під час аналізу випадкових процесів має стаціонарний процес X(t) з нульовим середнім m_x = 0, жодна із гармонічних складових якого не корелюється ні з якою іншою складовою, крім самої себе.

Кореляційну функцію такого процесу можна задати у вигляді

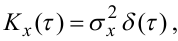(4.56)

де δ(t) — дельта-функція Дірака, яка, нагадаємо для зручності, має такі властивості:

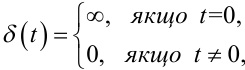(4.57)

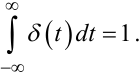(4.58)

Якщо підставити (4.56) у (4.53), то отримаємо:

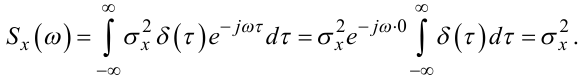(4.59)

Із (4.59) випливає, що спектр цього процесу є рівномірним від -∞ до +∞, тобто у сигналі присутні всі частоти з амплітудами випадковими, але такими, які забезпечують дисперсію процесу в усіх часових перерізах на рівні σ_x². Процес із визначеними у такий спосіб властивостями називають білим шумом.

Пропускаючи білий шум через фільтр із заданими параметрами, що формують глибину кореляції складових, можна сформувати випадковий процес з будь-якими наперед заданими властивостями, тобто із білого шуму за допомогою частотного фільтра виділяти будь-який «колір».

Як це зробити практично, буде показано у наступному розділі.