4.3 Ідентифікація безперервних стохастичних ЛДС ЗП за допомогою рівняння Вінера-Хопфа

Нехай в лінійній безперервній системі з невідомими, але зосередженими параметрами має місце стохастичний процес, обумовлений дією на її вході ергодичного стаціонарного випадкового сигналу X(t) (рис. 4.12).

Рисунок 4.12 — Умовне представлення безперервної стохастичної ЛДС ЗП у вигляді «чорного ящика»

Зрозуміло, що вихідний сигнал Y(t) системи теж буде ергодичним стаціонарним процесом.

Припустимо, що вдалося зафіксувати центровані реалізації x^*(t) та y^*(t) випадкових процесів X(t), Y(t) на одному і тому ж проміжку часу T (див. рис. 4.9). Незалежно від характеру сигналів x(t), y(t) для центрованих реалізацій x^*(t), y^*(t) є справедливою згортка

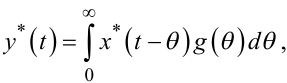(4.60)

де g(t) — вагова (імпульсна перехідна) функція безперервної ЛДС ЗП, для якої x(t) є вхідним, а y(t) — вихідним сигналами.

Якщо рівняння (4.60) є справедливим для довільного моменту часу t, то воно залишається справедливим і для моменту часу t + τ, тобто

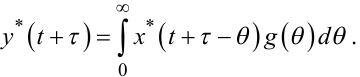(4.61)

Помножимо обидві частини рівняння (4.61) на x^*(t) і проінтегруємо їх у межах від нуля до T - τ, розділивши результат інтегрування на T - τ. Внаслідок цих дій отримаємо:

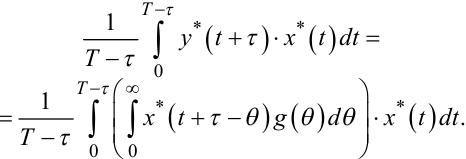(4.62)

Порівнюючи ліву частину рівняння (4.62) з виразом (4.51), бачимо, що це є оцінка K^*_yx(τ) взаємної кореляційної функції ергодичних випадкових процесів X(t), Y(t).

Як відомо з курсу математики, порядок інтегрування у подвійних інтегралах можна міняти місцями, оскільки ця операція є лінійною.

З урахуванням цих двох зауважень перепишемо рівняння (4.62) таким чином:

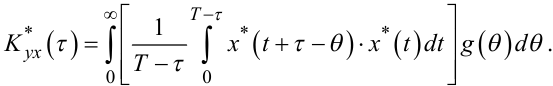(4.63)

Порівнюючи вираз, що стоїть у квадратних дужках у правій частині (4.63), з рівнянням (4.37), бачимо, що це є оцінка K^*_x(τ - θ) кореляційної функції ергодичного випадкового процесу X(t). З урахуванням цього зауваження перепишемо рівняння (4.63) таким чином:

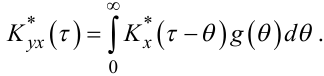(4.64)

У правій частині рівняння (4.64), як і у правій частині рівняння (4.60), теж маємо згортку, але, на відміну від стохастичної згортки в (4.60), в (4.64) маємо вже детерміновану згортку, оскільки у теоретичному плані кореляційна функція випадкового процесу є, на відміну від нього самого, функцією детермінованою. Рівняння (4.64), яке у різний час незалежно один від одного і різними способами вивели відомі математики Вінер і Хопф, так і називають рівнянням Вінера-Хопфа.

Оскільки Вінер прийшов до цього рівняння, розв’язуючи задачу оптимальної фільтрації «зашумленого» сигналу x(t) фільтром із ваговою характеристикою g(t) шляхом мінімізації квадратичного критерію якості J, який має вигляд

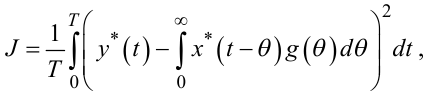(4.65)

то можна стверджувати, що функція g(t), якщо вона знайдена шляхом розв’язання рівняння Вінера-Хопфа (4.64), є не просто одним із розв’язків цього рівняння, а розв’язком оптимальним за квадратичним критерієм якості (4.65).

У першій частині цього посібника показано, що вагова характеристика g(t) безперервної лінійної системи з зосередженими параметрами є однією із форм подання математичної моделі цієї системи, а тому, визначаючи цю характеристику шляхом розв’язання рівняння Вінера-Хопфа (4.64), тим самим розв’яжемо задачу ідентифікації безперервної лінійної динамічної системи з зосередженими параметрами, в якій протікає стохастичний процес.

Способів розв’язання рівняння (4.64), яке відносять до класу некоректних, існує дуже багато.

Найпростішим є спосіб розв’язання системи алгебраїчних рівнянь відносно числових значень g(θ₀),g(θ₁),g(θ₂),..., g(θ_n-1), які формуються з інтегрального рівняння (4.64) переходом від безперервного інтегрування у нескінченних границях до знаходження скінченних сум відносно фіксованих зсувів τ₀,τ₁,...,τ_n-1, тобто

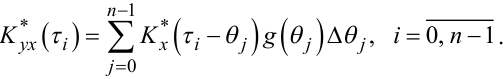(4.66)

Слід запам’ятати, що для збіжності розв’язку систем рівнянь (4.66) необхідно квантувати час θ і зсув τ рівними відрізками, тобто

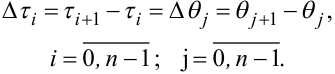(4.67)

Слід пам’ятати також і про те, що згідно з (4.39)

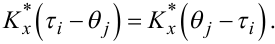(4.68)

Для того, щоб розв’язати рівняння Вінера-Хопфа (4.64) у частотній області, помножимо його ліву і праву частини на e^-jωτ і проінтегруємо у нескінченних границях. Виконавши це, маємо

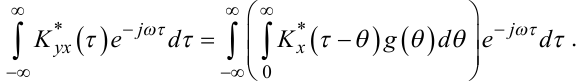(4.69)

Порівнюючи ліву частину рівняння (4.69) з виразом (4.55), бачимо, що це є оцінка взаємної спектральної густини S^*_yx(jω) випадкових процесів X(t) та Y(t).

У правій частині рівняння (4.69) здійснимо заміну змінних. Покладемо, що

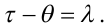(4.70)

Тоді матимемо:

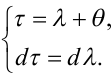(4.71)

З урахуванням цієї заміни перепишемо рівняння (4.69) таким чином:

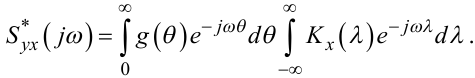(4.72)

Оскільки

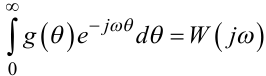(4.73)

— це амплітудно-фазова частотна характеристика (АФЧХ) системи, визначення якої здійснено у першій частині посібника, то, з урахуванням виразу (4.53), рівняння (4.72) можна переписати у вигляді

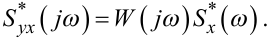(4.74)

Легко бачити, що розв’язком рівняння Вінера-Хопфа (4.64) у частотній області є вираз

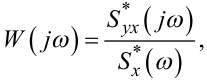(4.75)

який визначає АФЧХ W(jω) системи через оцінки спектральних густин S_x^*(ω), S_yx^*(ω) випадкових процесів X(t, Y(t, що мають місце на вході та виході цієї системи.

Слід зазначити, що простий за зовнішніми ознаками розв’язок рівняння Вінера-Хопфа у вигляді (4.75) досить серйозні труднощі свого отримання переносить на знаходження аналітичного виразу для оцінки взаємної спектральної густини S_yx^*(ω) по несиметричній кривій K_yx^*(τ), для якої дуже непросто здійснити зручну для інтегрування при перетворенні за Фур’є аналітичну апроксимацію.

Як буде показано у наступному підрозділі, найзручнішим способом розв’язання рівняння Вінера-Хопфа є Фур’є-інтегральний метод ідентифікації (ФІМІ), основи якого для детермінованих систем викладені у першій частині посібника.