4.4.1 Отримання основних розрахункових співвідношень та побудова алгоритму ідентифікації

Нехай τ_вх — час взаємної кореляції вхідного x(t) і вихідного y(t) стохастичних сигналів системи (див. рис. 4.10, 4.12). І нехай виконуються передумови, визначені вище.

Тоді на відрізку [-τ_вх,τ_вх] обидві кореляційні функції K_x(τ) і K_yx(τ) можна розкласти у ряди Фур’є у вигляді:

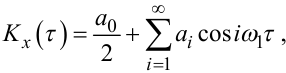(4.76)

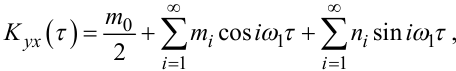(4.77)

де

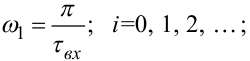
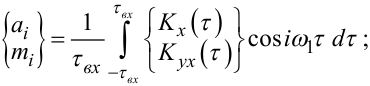(4.78)

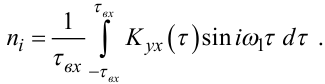(4.79)

Функція K_x(τ) є парною (див. рис. 4.8), тому її розкладання у ряд Фур’є не містить синусоїд.

Підставляючи ряди (4.76), (4.77) у рівняння Вінера-Хопфа (4.64), після тривіальних перетворень отримаємо:

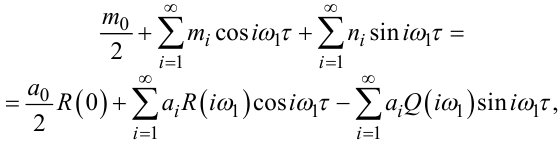(4.80)

де R(iω₁) та Q(iω₁) — значення, відповідно, дійсної та уявної характеристик ЛДС ЗП, взятих при значеннях частоти ω₁:

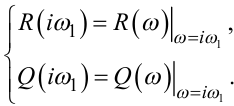(4.81)

З тотожності (4.80), як наслідок, маємо:

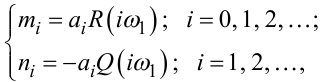(4.82)

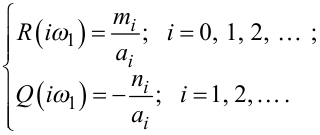(4.83)

Отриманням формул (4.83) закінчується перший етап побудови алгоритму параметричної ідентифікації стохастичних безперервних ЛДС ЗП за допомогою ФІМІ.

Другий етап побудови алгоритму у цій задачі є ідентичним другому етапу розв’язання задачі, описаної у підрозділі 3.3 першої частини посібника. Відмінність полягає лише у тому, що R(iω₁), Q(iω₁) у нашому випадку визначаються за формулами (4.83) цього підрозділу, а не за формулами (3.23), (3.24) першої частини посібника — всі інші формули і дії збігаються, тому немає потреби їх знову наводити.