5.1 Часові ряди та їх основні характеристики

У першій частині цього посібника та у попередніх розділах другої частини викладені методи побудови математичних моделей ЛДС ЗП, придатних для аналізу процесів у цих системах у даний момент часу та синтезу систем автоматичного керування ними.

Але не менш важливою є задача прогнозування розвитку процесу у системі в майбутньому, для розв’язання якої ті математичні моделі, що вже розглянуті, непридатні.

На сьогоднішній день найбільш ефективними математичними моделями, за допомогою яких можна прогнозувати розвиток процесів, є ті, під час побудови яких використовуються часові ряди.

Нагадаємо, що часовий ряд — це сукупність значень випадкового процесу, взятих через рівні проміжки часу t. Позначимо цю сукупність символом z_t.

Фактично z_t — це є дискретний у часі випадковий процес.

Задача прогнозу полягає в тому, що, знаючи значення процесу у момент t, необхідно спрогнозувати його значення в момент t + l, де l — час упередження. Щоб відрізняти прогнозне значення процесу від дійсного, дійсне значення часового ряду у момент t + l позначають символом z_t+l, а прогнозне значення — символом z_t(l).

Зрозуміло, що точно спрогнозувати значення випадкового процесу, яким є часовий ряд, неможливо в принципі, а тому прогноз здійснюють, домагаючись мінімуму якогось критерію адекватності прогнозної моделі.

Якщо значення t є малим (1, 2 кроки), то одним із таких критеріїв може бути дисперсія відхилення z_t(l) від z_t+l, яка повинна бути для оптимальної моделі прогнозу мінімальною, тобто

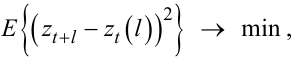(5.1)

де E — символ операції математичного очікування.

У наступному розділі розглянемо й інші критерії оптимальності моделей.

Як і будь-який інший випадковий процес, часовий ряд z_t може бути стаціонарним (рис. 5.1,а) або нестаціонарним (рис. 5.1,б).

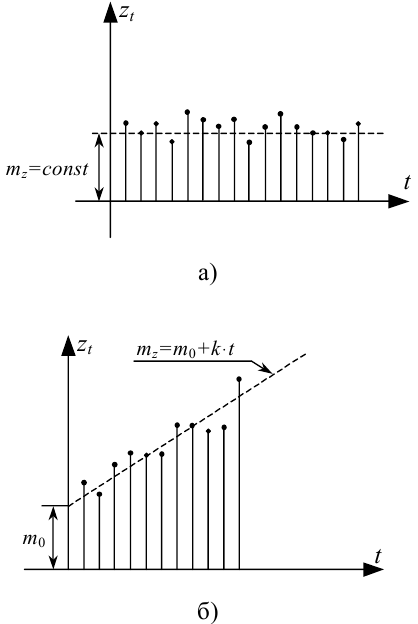
Рисунок 5.1 — Графіки реалізації стаціонарного (а) та нестаціонарного (б) часових рядів

Для стаціонарного часового ряду характерною є рівновага його значень z_t біля середнього значення m_z, яке є константою.

Для нестаціонарного часового ряду ковзне середнє значення m_z(t) процесу є функцією часу t, як показано на рис. 5.1,б.

Введемо ряд корисних операторів, які будуть потрібними у подальшому.

1. Оператор B зсуву назад на одну одиницю часу. Цей оператор формує рівняння

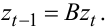(5.2)

Зрозуміло, що згідно з (5.2) справедливим є і рівняння

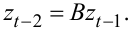(5.3)

Підставляючи значення z_t-1 із (5.2) в (5.3), отримаємо:

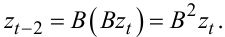(5.4)

Узагальнюючи (5.4), маємо

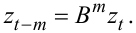(5.5)

2. Оператор F зсуву вперед на одну одиницю часу. Цей оператор формує рівняння

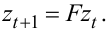(5.6)

Зрозуміло, що згідно з (5.6) справедливим є і рівняння

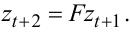(5.7)

Підставляючи значення z_t+1 із (5.6) в (5.7), отримаємо:

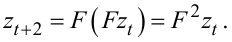(5.8)

Узагальнюючи (5.8), маємо:

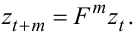(5.9)

3. Різницевий оператор ∇ із зсувом назад на одну одиницю часу. Цей оператор формує рівняння

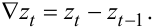(5.10)

Підставляючи значення z_t-1 із (5.2) в (5.10), отримаємо:

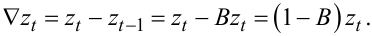(5.11)

Із (5.11) випливає, що

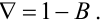(5.12)

4. Різницевий оператор Δ із зсувом вперед на одну одиницю часу. Цей оператор формує рівняння

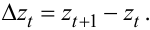(5.13)

Підставляючи значення z_t+1 із (5.6) в (5.13), отримаємо:

(5.14)

Із (5.14) випливає, що

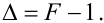(5.15)

5. Оператор суми S. Цей оператор формує рівняння

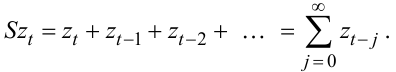(5.16)

Підставляючи значення z_t-m із (5.5) в (5.16), отримаємо:

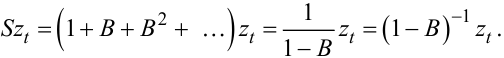(5.17)

Примітка. Під час виведення співвідношення (5.17) було використано формулу суми членів нескінченно спадної геометричної прогресії зі знаменником B, який за умови розгляду його як числа та умови збіжності ряду (5.16) повинен бути меншим одиниці.

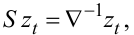(5.18)

або

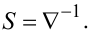(5.19)

Таким чином, оператор суми є оберненим різницевому оператору із зсувом назад.