5.2 Синтез моделі стаціонарного часового ряду на основі лінійного фільтра

Послідовність некорельованих і розподілених нормально випадкових імпульсів at з нульовим середнім значенням і дисперсією

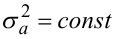(5.20)

називають дискретним білим шумом.

Спробуємо використати імпульси білого шуму at для побудови моделі часового ряду z_t у такий спосіб

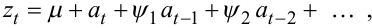(5.21)

де μ — рівень відліку (середнє значення) часового ряду z_t, а ψ_k, k = 1,2,... — коефіцієнти ваги імпульсів білого шуму, з якими вони входять до суми (5.21).

Здійснимо операцію центрування часового ряду zt , віднявши від zt середнє значення μ. Для центрованого часового ряду

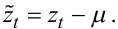(5.22)

Із (5.21) отримаємо:

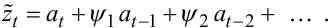(5.23)

Використовуючи для імпульсів a_t-m співвідношення (5.5), із (5.23) маємо:

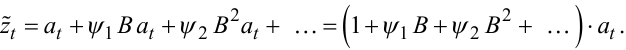(5.24)

Позначимо

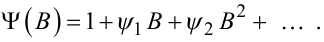(5.25)

З урахуванням (5.25) співвідношення (5.24) можна записати таким чином:

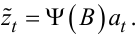(5.26)

Функцію Ψ(B) називають передаточною функцією фільтра, який перетворює послідовність імпульсів білого шуму at у часовий ряд з заданими властивостями (рис. 5.2).

Коефіцієнти фільтра ψ_k, k = 1, 2,... підбираються у процедурі мінімізації критерію (5.1) при l = 0.

Рисунок 5.2 — Структурна схема лінійного фільтра