5.3 Модель стаціонарного часового ряду на основі авторегресії

З філософської точки зору модель регресії — це модель «з оглядкою назад, у бік, звідки прийшов»; тобто це модель, яка встановлює значення якоїсь координати процесу у даний момент часу за її незалежними складовими, визначеними у попередній момент. Кількість врахованих складових визначає порядок регресії.

Виходячи з даного трактування, модель авторегресії — це модель, яка встановлює значення якоїсь координати процесу у даний момент часу на основі своїх попередніх значень. Кількість врахованих попередніх значень визначає порядок авторегресії.

Для центрованого часового ряду модель авторегресії порядку p (скорочено: АР(p)) можна записати у вигляді:

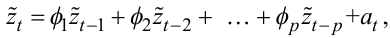(5.27)

де a_t — імпульс білого шуму, означення якому дано вище.

З урахуванням співвідношення (5.5) вираз (5.27) можна переписати таким чином:

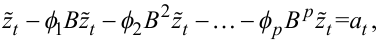або

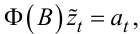(5.28)

де Ф(B) — оператор авторегресії порядку p:

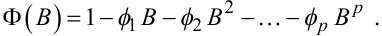(5.29)

Скористаємось далі тотожністю

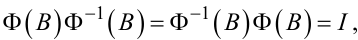(5.30)

в якій I — одиничний оператор; оператор Ф_-1(B) — обернений до оператора Ф(B).

Помноживши на Ф_-1(B) зліва рівняння (5.28), отримаємо:

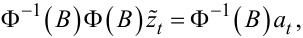(5.31)

або (з урахуванням (5.30)):

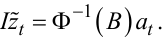(5.32)

Оскільки перемноження на одиничний оператор результату не змінює, то (5.32) можна записати і так:

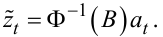(5.33)

Порівнюючи (5.33) з (5.25), можна стверджувати, що

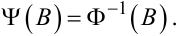(5.34)

Отже, отримавши за реалізацією досліджуваного часового ряду z_t оператор авторегресії Ф(B), що зробити, як буде показано далі, нескладно, та визначивши оператор Ф_-1(B), обернений до Ф(B), що теж досить просто, тим самим одночасно визначаємо і передаточну функцію Ψ(B) лінійного фільтра, який з білого шуму a_t формує потрібний часовий ряд z_t.

Звертаємо увагу на те, що у цьому випадку Ψ(B) знаходиться без мінімізації критерію (5.1) при l = 0, про що йшла мова в кінці попереднього підрозділу.

Під час розв’язання задачі ідентифікації моделі часового ряду z_t на основі авторегресії порядку p необхідно визначити p + 2 невідомих, якими є коефіцієнти ф₁,ф₂,...,ф_p оператора Ф(B), середнє значення μ процесу z_t та дисперсія σ_a² білого шуму a_t.

Про те, як розв’язати цю задачу, мова буде йти у підрозділах 5.8, 5.9.