5.4 Модель стаціонарного часового ряду на основі ковзного середнього

В моделі лінійного фільтра (5.22) значення часового ряду z_t визначаються через зважену суму поточного та попередніх імпульсів білого шуму a_t.

Характерною особливістю передаточної функції Ψ(B) (5.24) фільтра є те, що теоретично вона має нескінченну кількість членів, що створює певні незручності у разі використання цієї моделі.

Тому цікавою виявилась пропозиція будувати модель часового ряду z_t на основі скінченної множини потужністю q зважених імпульсів білого шу- му a_t у вигляді

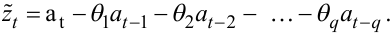(5.35)

Оскільки у співвідношенні (5.35) використовується q попередніх значень білого шуму a_t-i, i = 1, q, які зважено віднімаються від поточного імпульсу a_t, то це співвідношення фактично задає «ковзне середнє» яке «зміщується» вздовж послідовності a_t з ростом t, утримуючи в собі при «зміщенні» одну і ту ж кількість членів

Застосовуючи до імпульсів a_t-m ідеологію співвідношення (5.5), із (5.35) отримуємо:

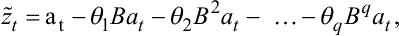(5.36)

або

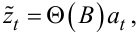(5.37)

де Θ(B) — оператор ковзного середнього

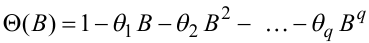(5.38)

порядку q.

Співвідношення (5.37), (5.38) задають модель стаціонарного часового ряду z_t у вигляді моделі ковзного середнього порядку q (скорочено: модель КС(q) ).

При розв'язанні задачі ідентифікації моделі часового ряду z_t на основі ковзного середнього порядку q необхідно визначити q + 2 невідомих, якими є коефіцієнти θ₁,θ₂₁,...,θ_q оператора Θ(B), середнє значення μ процесу z_t та дисперсія σ_a² білого шуму a_t.