5.5 Комбінована модель стаціонарного часового ряду на основі авторегресії — ковзного середнього

В моделі часового ряду z_t на основі авторегресії порядку p у формуванні поточного значення ряду бере участь лише один поточний імпульс білого шуму a_t. Природно припустити, що якщо від цього імпульсу a_t відняти зважену суму q попередніх значень білого шуму, то отримаємо модель, яка буде враховувати більш «тонкі» моменти випадкового процесу і більш адекватно віддзеркалюватиме його властивості, оскільки крім авторегресії ця модель буде враховувати ще й ковзне середнє процесу.

Така модель часового ряду z_t носить назву модель авторегресії — ковзного середнього порядку (p, q) (скорочено: модель АРКС(p, q)) і має вигляд:

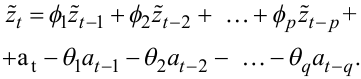(5.39)

Перенісши всі члени з , i=1, p у ліву частину рівняння (5.39) та виконавши вже відомі перетворення, отримаємо рівняння

(5.40)

в якому оператори Ф(B) та Θ(B) визначаються формулами (5.29), (5.38).

Рівняння (5.40) і є основною формою моделі часового ряду z_t на основі АРКС(p, q).

Для ідентифікації цієї моделі необхідно визначити p + q + 2 невідомих, якими є коефіцієнти ф_i, i = 1, p оператора Ф(B), коефіцієнти θ_j, j = 1, q оператора Θ(B), середнє значення μ процесу z_t та дисперсія σ_a² білого шуму a_t.