5.6 Модель нестаціонарного часового ряду на основі авторегресії — проінтегрованого ковзного середнього

Всі моделі часових рядів, що побудовані у попередніх підрозділах, базувались на умові стаціонарності цих рядів. Але у повсякденному житті постійно стикаємося і з нестаціонарними випадковими процесами. Наприклад, процес пуску потужного електропривода, який працює на навантаження випадкового характеру (екскавація, конвеєрна доставка кускової руди з шахти, перемелювання рудних матеріалів у дробарках та млинах тощо), має досить суттєві проміжки нестаціонарності.

Покажемо, що такі нестаціонарні випадкові процеси, які при їх дискретизації перетворюються на часові ряди, можна досить адекватно описувати за допомогою моделі авторегресії — проінтегрованого ковзного середнього.

Припустимо, що у моделі АРКС(p, q), поданій виразом (5.40), оператор Ф(B) має d кратних коренів, що дорівнюють одиниці.

У цьому випадку, згідно з теоремою Вієта, оператор Ф(B) можна записати у вигляді

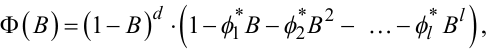(5.41)

де

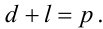(5.42)

Позначимо

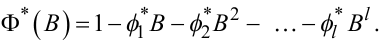(5.43)

З урахуванням (5.41) та (5.43) рівняння (5.40) можна переписати так:

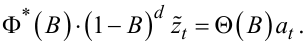(5.44)

Оскільки згідно з (5.12)

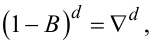(5.45)

тобто (1 - B)^d є різницевим оператором із зсувом назад порядку d, то рівняння

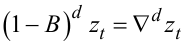(5.46)

задає нову змінну w_t, яка пов'язана з z_t співвідношенням

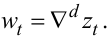(5.47)

Підставляючи (5.47) у рівняння (5.44), отримуємо:

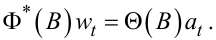(5.48)

Очевидно, що (5.48) задає модель АРКС(l, q) відносно w_t, яке можна переписати і так

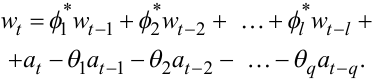(5.49)

Рівняння (5.47), (5.48) задають модель нестаціонарного часового ряду z_t у вигляді авторегресії — проінтегрованого ковзного середнього порядку (l, q, d). Скорочено: модель АРПКС(l, q, d).

Звертаємо увагу на те, що вже перша різниця ∇z_t значень будь-якого нестаціонарного часового ряду z_t має менший ступінь нестаціонарності, ніж сам часовий ряд z_t. Ще менший ступінь нестаціонарності матиме друга різниця ∇²z_t, яка є різницею перших різниць ∇(∇z_t) цього часового ряду z_t.

Підвищуючи порядок d різниці ∇^dz_t, рано чи пізно дійдемо до такого її значення w_t, яке вже являтиме собою стаціонарний часовий ряд відносно w_t. На рис. 5.3 наведена графічна інтерпретація цього факту.

Зрозуміло, що з моделі АРПКС(l, q, d) (5.47), (5.48) при d = 0 отримаємо модель АРКС(p, q).

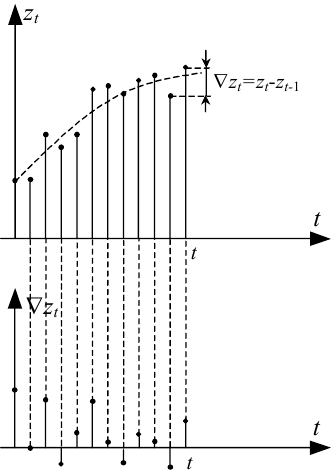
Рисунок 5.3 — Графічна інтерпретація перетворення нестаціонарного часового ряду z_t у стаціонарний часовий ряд для його різниці ∇z_t

Дамо пояснення чому у назві моделі АРПКС(l, q, d) має місце слово «проінтегроване» стосовно ковзного середнього.

Нагадаємо, що оберненим оператором для ∇ є оператор суми (або інтегрування) S (5.19). Тому, отримавши w_t із рівняння (5.48), для переходу до часового ряду z_t необхідно координату w_t проінтегрувати d разів, оскільки, домножуючи рівняння (5.47) зліва на ∇^-d, маємо:

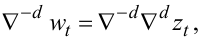(5.50)

або

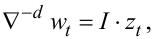(5.51)

звідки, з урахуванням (5.19), матимемо:

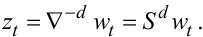(5.52)

Зрозуміло, що найскладнішим завданням під час використання моделі АРПКС(l, q, d) є визначення чисельного значення параметра інтегрування d, або, в інших термінах, визначення кількості різниць, які треба послідовно взяти від нестаціонарного часового ряду z_t, щоб перетворити його у стаціонарний ряд відносно якоїсь різниці цього ряду.