5.7 Автоковаріація та автокореляція часового ряду

Автоковаріацією γ_k часового ряду z_t з затримкою k називають вираз

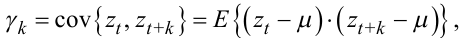(5.53)

в якому E — символ обчислення математичного очікування від виразу, що стоїть у фігурних дужках.

Зрозуміло, що

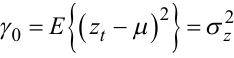(5.54)

— дисперсія часового ряду z_t.

Для отримання статистичної оцінки γ^*_k автоковаріації γ_k використовують вираз

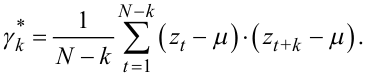(5.55)

Автоковаріація γ_k характеризує ступінь лінійного зв'язку між значеннями часового ряду z_t та z_t+k.

Зрозуміло, що

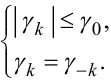(5.56)

Автокореляцією ρ_k часового ряду z_t із затримкою k називають вираз

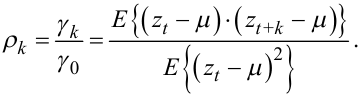(5.57)

Для довільної автокореляції ρ_k справедливими є такі співвідношення:

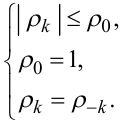(5.58)

Вся можлива сукупність γ_k є автоковаріаційною функцією часового ряду z_t. Вона належить до класу решітчастих функцій. Аналогічно сукупність всіх значень ρ_k задає автокореляційну функцію часового ряду z_t.

Приклад графіка автокореляційної функції ρ_k наведено на рис. 5.4.

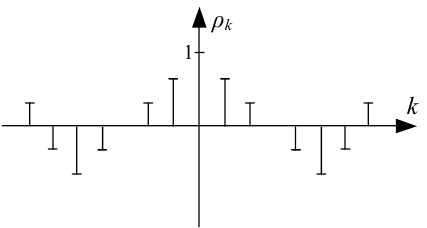
Рисунок 5.4 — Один із можливих графіків автокореляційної функції ρ_k, k = -N,N