5.8 Рівняння Юла-Уокера

Рівняння Юла-Уокера дають відповідь на запитання: «А як же визначити, скажімо, коефіцієнти авторегресії у моделі часового ряду у формі АР(p)?»

Для їх синтезу спочатку помножимо вираз (5.26) на . У результаті цього отримаємо:

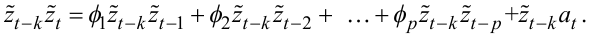(5.59)

Зробимо у (5.59) заміну дискретної змінної, поклавши

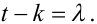(5.60)

Отримаємо:

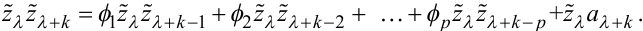(5.61)

Знайдемо математичне очікування E від обох частин рівняння (5.61).

Отримаємо:

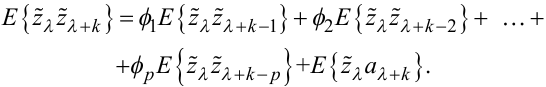(5.62)

Враховуючи (5.22) та (5.53), із (5.62) маємо:

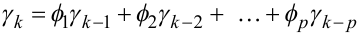(5.63)

для всіх k від 1 до p.

Але при k = 0 з урахуванням (5.56) отримаємо ще одне рівняння:

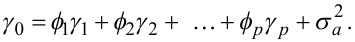(5.64)

Відсутність результатів обчислення математичного очікування у рівняннях (5.63) та їх присутність у рівнянні (5.64) у вигляді дисперсії білого шуму σ_a² пояснюється тим, що згідно з властивостями білого шуму кожний його імпульс корелюється (взаємпов'язується) лише сам із собою і зовсім не корелюється ні з яким іншим, навіть розміщеним у часі поряд. Тож

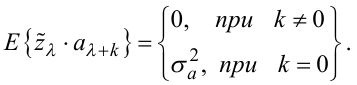(5.65)

З рівняння (5.64), з урахуванням (5.54), маємо:

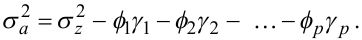(5.66)

Тож, якщо для реалізації стаціонарного часового ряду z_t довжиною N вже обчислені оціночні середнє значення μ і дисперсія σ_a² за відомими формулами

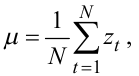(5.67)

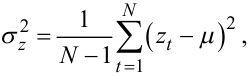(5.68)

знайдені якимсь чином коефіцієнти ф₁,ф₂,...,ф_p і обчислені за формулою (5.55) автоковаріації γ₁,γ₂,...,γ_p, тоді знайти дисперсію білого шуму σ_a² за формулою (5.66) зовсім нескладно.

Перш ніж викласти алгоритм отримання числових значень коефіцієнтів γ₁,γ₂,...,γ_p, розділимо всі рівняння системи (5.63) на σ₀

У результаті цього отримаємо систему рівнянь вже не відносно автоковаріацій σ_k, k = 1, p, а відносно автокореляцій ρ_k, k = 1, p, тобто систему

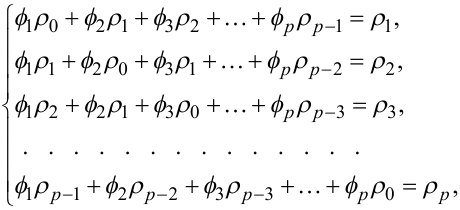(5.69)

або у матричній формі

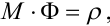(5.70)

де матриці M(p × p), Ф(p × 1), ρ(p × 1) мають вигляд

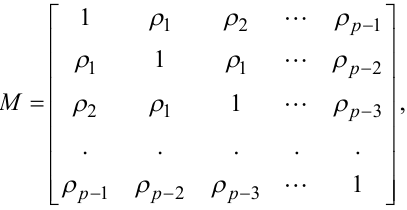
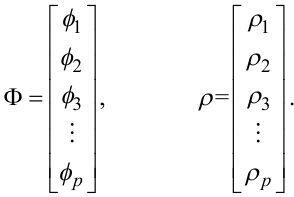
У рівняннях (5.70) невідомими є значення коефіцієнтів ф₁,ф₂,...,ф_p.

Для розв'язання системи (5.70) спочатку визначаємо матрицю M^-1, яка є оберненою матриці M. Потім множимо матричне рівняння (5.70) зліва на M^-1. У результаті цього отримуємо:

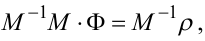(5.71)

або

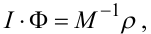(5.72)

і остаточно

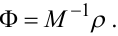(5.73)

Рівняння (5.69), (5.70) носять назву рівнянь Юла-Уокера. Їх розв'язок у вигляді (5.73) дозволяє за попередньо обрахованими автокореляціями ρ_k, k = 1,p часового ряду z_t визначити вектор Ф(p × 1) коефіцієнтів ф₁,ф₂,...,ф_p оператора регресії у моделі АР(p).