5.9 Приклад ідентифікації дискретної ЛДС ЗП на основі моделей часових рядів

Розглянемо процес z(t) формування струму якоря електродвигуна системи електропривода конвеєра, на який з бункера надходить вугілля кусками різного об'єму та форми для транспортування його до дробарки.

У зв'язку з тим, що кількість вугілля, яке надходить з бункера на конвеєр у кожний момент часу, є величиною випадковою, то і момент навантаження на валу електродвигуна теж буде величиною випадковою, відповідною масі вугілля, яке в даний момент часу знаходиться на конвеєрі. У свою чергу, такий же випадковий характер буде мати і обертальний момент електродвигуна, який врівноважує момент навантаження, і струм якоря електродвигуна, який створює обертальний момент.

Якщо вимірювати струм якоря електродвигуна лише через рівні відрізки часу t, то матимемо реалізацію часового ряду z_t, наведену у табл. 5.1.

Таблиця 5.1 — Реалізація часового ряду z_t струму якоря електродвигуна системи електропривода конвеєра

Побудуємо математичні моделі цього часового ряду z_t на основі авторегресії 1-го, 2-го та 3-го порядків, що мають вигляд:

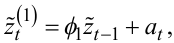(5.74)

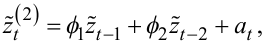(5.75)

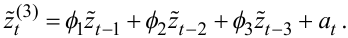(5.76)

Почнемо розв'язання задачі ідентифікації часового ряду z_t зі знаходження оцінок його середнього значення μ, дисперсії та автоковаріацій γ₁, γ₂, γ₃

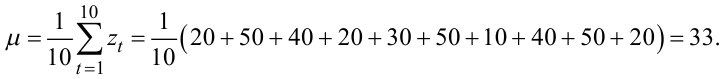(5.77)

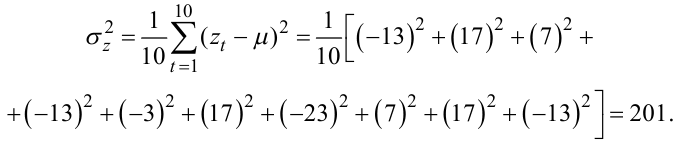(5.78)

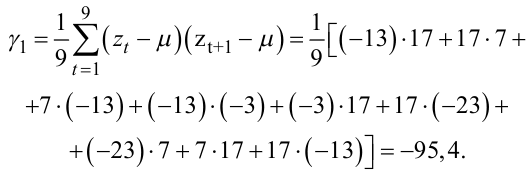(5.79)

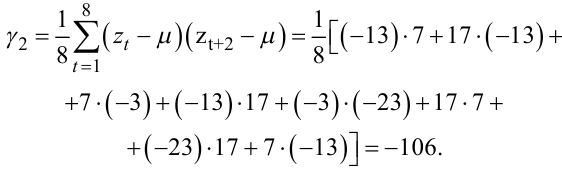(5.80)

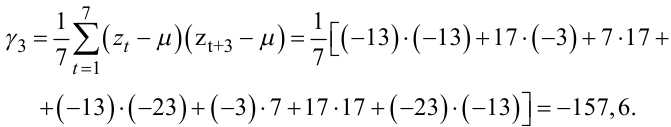(5.81)

Тепер підрахуємо автокореляції ρ₁, ρ₂, ρ₃.

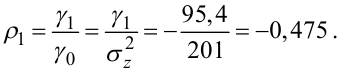(5.82)

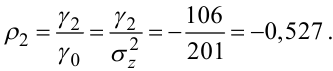(5.83)

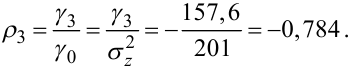(5.84)

Запишемо рівняння Юла-Уокера для моделі АР(1) (5.74):

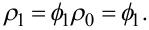(5.85)

Підставляючи значення ρ1 із (5.82) в (5.85), отримаємо:

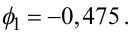(5.86)

Тож модель АР(1) для часового ряду z_t, заданого табл. 5.1, буде мати вигляд

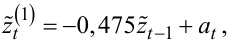(5.87)

де a_t — імпульс білого шуму з дисперсією (згідно з виразом (5.66)):

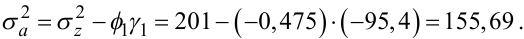(5.88)

Таким чином, якщо потрібно за допомогою моделі (5.87) спрогнозувати одинадцяте значення часового ряду z_t, заданого табл. 5.1, то повинні його десяте значення перемножити на (–0,475) і до цього результату додати значення імпульсу білого шуму a_t, генерованого комп'ютером за стандартною програмою, в яку треба лише задати значення дисперсії цього шуму, визначене за формулою (5.88), тобто = 155,69.

Тепер запишемо рівняння Юла-Уокера для моделі АР(2) (5.75):

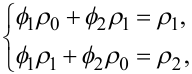(5.89)

або

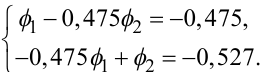(5.90)

Розв'язуючи цю систему двох рівнянь з двома невідомими ф₁, ф₂, отримаємо:

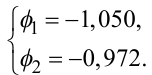(5.91)

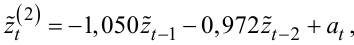(5.92)

де a_t — імпульс білого шуму з дисперсією (згідно з виразом (5.66)):

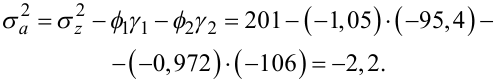(5.93)

Але дисперсія ніколи не може мати від'ємний знак, отже, отримання результату (5.93) свідчить про неадекватність моделі АР(2) для часового ряду z_t, заданого табл. 5.1.

Зрозуміло, що ще гірший результат принесе спроба моделювати цей часовий ряд за допомогою АР(3) (5.76).

Тож зупиняємося на моделі (5.87).

Але, якби було б більшим за нуль, тоді і друга модель теж мала б право на існування. І для того, щоб здійснити вибір, необхідно було б знайти суму квадратів відхилень, спрогнозованих за допомогою моделі значень часового ряду від отриманих експериментально. Та модель, для якої ця сума відхилень виявиться найкращою, і буде оптимальною для часового ряду, який моделюється.

У цьому підрозділі розглянуто приклад розв'язання задачі ідентифікації часового ряду лише на основі моделі авторегресії.

Всім, хто забажає використовувати інші моделі, рекомендуємо звернутись до книги Дж. Бокса, Г. Дженкінса «Анализ временных рядов. Прогноз и управление» (Вип. 1) [6], в якій розглянуто приклади використання всіх інших моделей