6.2 Клас математичних моделей, в якому здійснюватиметься ідентифікація динамічної системи

Оскільки складні динамічні системи або мають в одному із своїх замкнутих контурів, наприклад, контурі управління, комп'ютер, або аналізуються чи оптимізуються з використанням комп'ютера, то найбільш загальною формою математичної моделі для адекватного описання процесів в них є різницеве рівняння, яке для ЛДС ЗП в символах рис. 6.1 матиме вигляд:

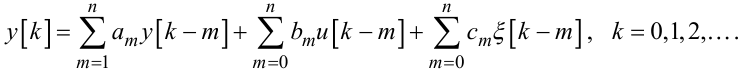(6.6)

Поява у правій частині рівняння (6.6) для визначення поточного значення вихідної координати y[k] суми ∑ зважених коефіцієнтами a_m попередніх n значень цієї вихідної координати y[k - m] обумовлена наявністю у динамічної системи пам'яті, створюваної внутрішніми накопичувачами енергії, яка вимагає при визначенні поточного значення вихідної координати враховувати у якійсь мірі її значення, набуті в попередні дискретні моменти часу. З цих же причин у правій частині рівняння (6.6) задіяні не лише поточні значення вхідного впливу u[k] та випадкового збурення ξ[k], а й зважені відповідними коефіцієнтами суми їх попередніх значень.

Якщо ввести оператор запізнення ρ як такий, що здійснює операцію

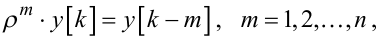(6.7)

то рівняння (6.6) можна привести до вигляду

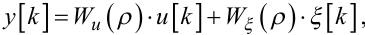(6.8)

де

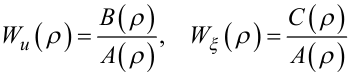(6.9)

— операторні передаточні функції ЛДС ЗП, в яких

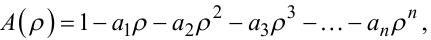(6.10)

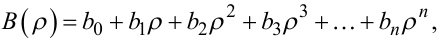(6.11)

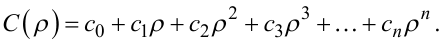(6.12)

Звертаємо увагу на те, що операторні передаточні функції W(ρ) ЛДС ЗП, хоч вони і отримані з використанням різницевих рівнянь, не є адекватними дискретним передаточним функціям W(z) цих систем, оскільки перші пов'язують між собою вхідну і вихідну координати, задані в дискретному часі, а другі пов'язують між собою ці координати, перетворені в функції комплексної змінної за допомогою Z-перетворення. Але вони легко перетворюються одна в одну з врахуванням того, що

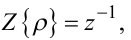(6.13)

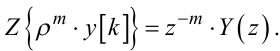(6.14)

Загальна структурна схема ЛДС ЗП, зв'язок між вхідним впливом u[k] та реакцією системи на нього y[k] в присутності випадкового збурення чи завади ξ[k] описується рівнянням (6.8), наведена на рис. 6.2.

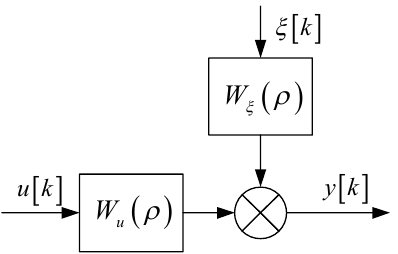
Рисунок 6.2 — Загальна структурна схема ЛДС ЗП з операторними моделями

Окрім загальної структурної схеми ЛДС ЗП, наведеної на рис. 6.2, при розв'язанні практичних задач ідентифікації часто використовують за наявності відповідних умов один із трьох спрощених її варіантів.

Розглянемо кожен із цих спрощених варіантів.

У першому варіанті (рис. 6.3) випадкове збурення ξ[k], назвемо його зовнішнім шумом, надходить на той же вхід системи, що і керуючий вплив u[k], тобто стохастичність системи породжується зашумленням вхідного сигналу.

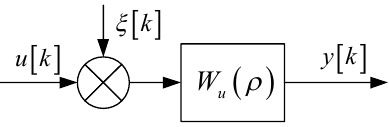
Рисунок 6.3 — Структурна схема ЛДС ЗП з зашумленим вхідним сигналом

Із структурної схеми, наведеної на рис. 6.3, легко бачити, що замість математичної моделі (6.8) у цьому випадку матимемо

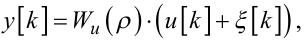(6.15)

або — з врахуванням (6.9) —

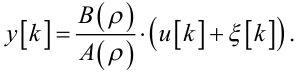(6.16)

Домножаючи обидві частини рівняння (6.16) на A(ρ) та враховуючи співвідношення (6.7), матимемо

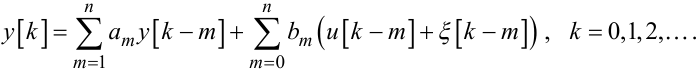(6.17)

У другому, спрощеному щодо структури (рис. 6.2), варіанті випадкове збурення ξ[k], яке теж буде зовнішнім шумом, надходить на вихід системи, додаючись до її реакції на вплив u[k] (рис. 6.4), тобто стохастичність системи породжується зашумленням вихідного сигналу.

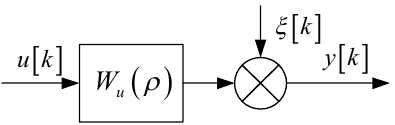
Рисунок 6.4 — Структурна схема ЛДС ЗП з зашумленим вихідним сигналом

Із структурної схеми, наведеної на рис. 6.4, легко бачити, що замість математичної моделі (6.8) у цьому випадку матимемо

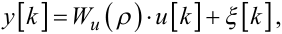(6.18)

або — з врахуванням (6.9) —

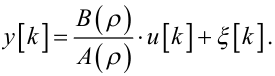(6.19)

Домножаючи обидві частини рівняння (6.19) на A(ρ) та враховуючи співвідношення (6.7), матимемо

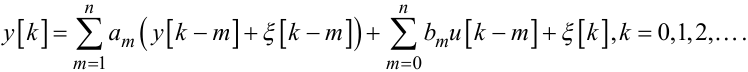(6.20)

У третьому, спрощеному щодо структури рис. 6.2, варіанті випадкове збурення ξ[k], яке тепер уже буде внутрішнім шумом, надходить на вихід системи, пройшовши через операторну передаточну функцію

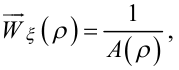(6.21)

яка залежить виключно лише від інерційних параметрів системи (рис. 6.5), тобто стохастичність системи породжується внутрішнім шумом системи.

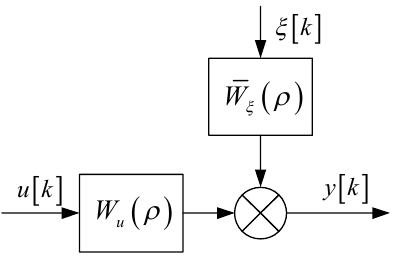
Рисунок 6.5 — Структурна схема ЛДС ЗП з внутрішнім шумом

Із структурної схеми, наведеної на рис. 6.5, легко бачити, що замість математичної моделі (6.8) у цьому випадку матимемо

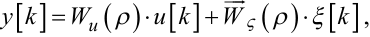(6.22)

або — з врахуванням (6.9) та (6.21) —

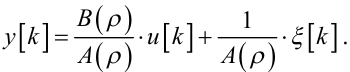(6.23)

Домножаючи обидві частини рівняння (6.23) на A(ρ) та враховуючи співвідношення (6.7), матимемо

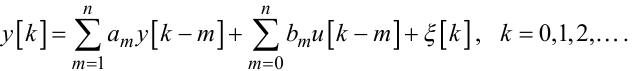(6.24)

Неважко помітити, що, якщо в рівняннях (6.9) покласти:

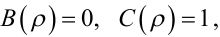(6.25)

то рівнянням (6.8) задаватиметься модель авторегресії, а якщо в рівняннях (6.9) покласти:

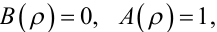(6.26)

то рівнянням (6.8) задаватиметься модель ковзного середнього.

У першому розділі цього навчального посібника формулою (1.13) була задана інтегральна модель лінійної динамічної системи з імпульсною перехі- дною характериcтикою g(t) та реакцією y(t) на вхідний вплив x(t).

В символах даного розділу для випадку безперервного часу і зашумленості вихідного сигналу, пов'язаної з похибками вимірювань і похибками обчислень, ця модель матиме вигляд

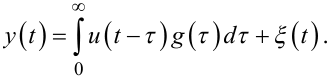(6.27)

Для дискретного часу t_k = kT при T = 1 інтегральне рівняння (6.27), яке було визначене для безперервних функцій, перетворюється на сумарне рівняння

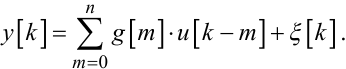(6.28)

Порівнюючи рівняння (6.28) з рівнянням (6.6) та його операторним аналогом (6.8), бачимо, що (6.28) може бути отриманим із (6.6) за умови, що

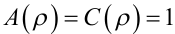(6.29)

та

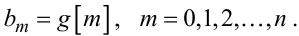(6.30)

Тож виходить, що і сумарне рівняння (6.28) може розглядатись як окремий випадок загального різницевого рівняння (6.6).

А позначаючи

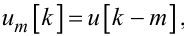(6.31)

бачимо, що рівняння (6.28) є регресією вихідної координати y[t] на вхідну координату u[t] та її попередні значення u_m[k].

Тож у подальшому рівняння (6.6) та його операторний аналог (6.8) і будуть розглядатись як основні математичні моделі ЛДС ЗП.

А ідентифікація ЛДС ЗП полягатиме у визначенні оцінок усіх коефіцієнтів в рівнянні (6.6) за інформацією про значення вхідного впливу та реакції системи на нього, виміряні в дискретні моменти часу. Всі ці коефіцієнти будемо позначати вектором , який є вектором-стовпцем, але який для зручності запишемо в транспонованому вигляді

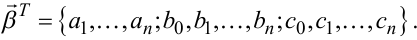(6.32)

Легко бачити із наведених різницевих математичних моделей ЛДС ЗП, що для динамічних систем з ковзним середнім завади виконується тотожність

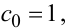(6.33)

а тому вектор буде мати порядок на одиницю менший від вектора, визначеного виразом (6.32); для динамічних систем з внутрішнім шумом і для динамічних систем з зашумленим вихідним сигналом крім тотожності (6.33) виконуватиметься ще й тотожність

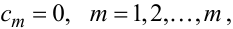(6.34)

а тому вектор матиме вигляд

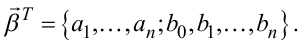(6.35)

Цілком очевидним є і те, що для ЛДС ЗП з зашумленим вхідним сигналом теж буде справедливим вираз (6.35).

Тож в багатьох практичних задачах ідентифікації доводиться визначати суттєво меншу кількість параметрів математичної моделі у порівнянні з тією, яка задається вектором (6.32).