6.3 Модельна конструкція, параметри якої можна змінювати

Наступним етапом після вибору структури моделі ЛДС ЗП є побудова модельної конструкції, настроюванням параметрів β^* якої можна визначити такі значення коефіцієнтів моделі ЛДС ЗП, за яких ця модель адекватно описувала б процеси, що протікають у динамічній системі. Різними авторами таких модельних конструкцій запропоновано чимало, але візьмемо ту, що використана Я. З. Ципкіним, а саме:

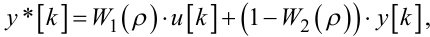(6.36)

в якій W1(ρ), W2(ρ) — поки що невідомі операторні передаточні функції, параметри яких можна настроювати, причому на em>W2(ρ) накладається умова

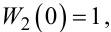(6.37)

що означає прогнозувальний характер моделі (6.36), оскільки нульовому значенню оператора запізнення ρ відповідає відсутність впливу останнього значення вихідної координати динамічної системи y[k] на вихідну координату модельної конструкції y^*[k].

Ще однією особливістю модельної конструкції (6.36) є відсутність в ній збурення ξ[k], що діє на динамічну систему, оскільки воно є випадковим з невідомими параметрами, а тому не може бути заведеним у конструкцію моделі, параметри якої настроюються.

Підставляючи (6.36) і (6.8) в (6.1), знайдемо, що для нев'язки ε[k] буде справедливим вираз

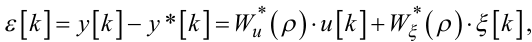(6.38)

де

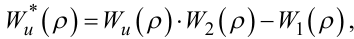(6.39)

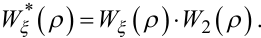(6.40)

Якщо за функцію втрат F(ε) візьмемо квадрат нев'язки, то критерієм адекватності модельної конструкції (6.36) динамічній системі, що ідентифікується, будуть виступати середні втрати, які є математичним очікуванням функції втрат і одночасно функціоналом Ф(•) від невідомих операторних передаточних функцій W₁(ρ), W₂(ρ), тобто

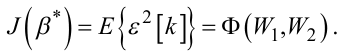(6.41)

Очевидно, що в разі оптимальної настройки коефіцієнтів моделі критерій (6.41) буде мати найменше значення, а це, в свою чергу, означає, що оптимальну структуру і оптимальні значення коефіцієнтів операторних передаточних функцій W₁(ρ), W₂(ρ) можна знайти, мінімізуючи функціонал Ф(•) за W₁ та W₂.

Згадуючи те, що (6.41) — це дисперсія нев'язки, яка є випадковою величиною, а також те, що дисперсію випадкової величини можна визначити за допомогою рівності Парсеваля через передаточні функції системи, які її формують, та спектральні густини вхідного впливу і завади, можна записати, що

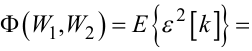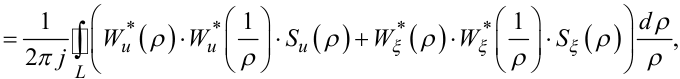(6.42)

де S_u(ρ) — спектральна густина керуючого впливу u[k], S_ξ(ρ) — спектральна густина завади ρ[k], а L -контур інтегрування на комплексній площині по колу одиничного радіуса з центром в початку системи координат.

Поставимо умову, щоб структура модельної конструкції, як і внутрішня структура динамічної системи, що ідентифікується, не залежали від керуючого впливу u[k]. Оскільки для пошуку цієї структури намагаємося використати функціонал Ф(•), то виставлена умова збігається з умовою, що цей функціонал не залежить від спектральної густини S_u(ρ). Але, у свою чергу, із правої частини виразу (6.42) випливає, що це можливо лише за умови, що

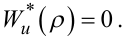(6.43)

При виконанні умови (6.43) функціонал Ф(•) стає залежним лише від W₂(ρ), оскільки, підставляючи (6.39) в (6.43), матимемо

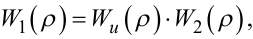(6.44)

а (6.42) перетворюється у

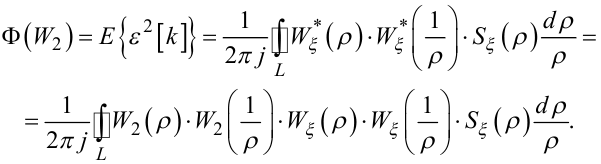(6.45)

Мінімізація цього функціонала зводиться до прирівнювання до нуля його першої варіації за W₂(ρ) та W₂ , яке приводить в силу ідентичності структури обох інтегралів, які при цьому формуються, та виразу (6.5), при виконанні якого матимемо

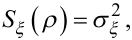(6.46)

до рівняння

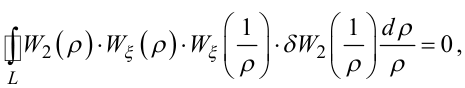(6.47)

в якому δW₂ — перша варіація операторної передаточної функ- ції W₂ .

Як відомо з теорії автоматичного управління, інтеграл в лівій частині рівняння (6.44) дорівнює нулю за виконання двох умов, одна з яких полягає в тому, щоб полюси усіх передаточних функцій, які характеризують ЛДС ЗП як по каналу проходження керуючого впливу так і по каналу проходження завади, знаходилися на комплексній площині всередині круга одиничного радіуса з центром в початку координат, а друга умова полягає в тому, щоб виконувалась рівність

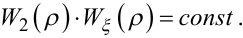(6.48)

Задаючи в рівнянні (6.48) ρ = 0 і враховуючи умову (6.37) та співвідношення (6.9), (6.10), (6.12), знайдемо, що

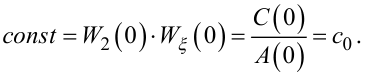(6.49)

Одразу ж зауважимо, що, як було показано вище, для більшості важливих для практики задач маємо

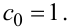(6.50)

Із (6.48) та (6.49) випливає, що

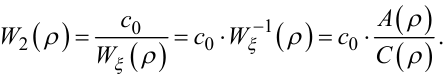(6.51)

А підставляючи в (6.44) вираз (6.51), знайдемо, що

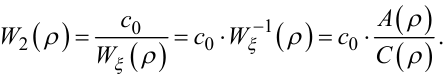(6.52)

Підстановка ж (6.51) і (6.52) в (6.36) приводить до оптимальної за середніми втратами структури математичної моделі ЛДС ЗП з придатними для настроювання параметрами у вигляді

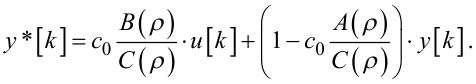(6.53)

Нагадаємо, що в явному вигляді A(ρ), B(ρ), C(ρ) наведені у виразах (6.10), (6.11), (6.12), а для більшості практичних задач ідентифікації справедливим є (6.50).

Якщо в моделі (6.53) перейти від операторів запізнення ρ до самих запізнень в аргументах вхідної і вихідної координат згідно з виразом (6.7), то отримаємо оптимальну різницеву модель ЛДС ЗП у вигляді

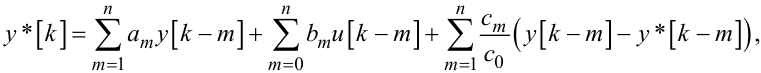(6.54)

або (для найбільш розповсюдженого випадку, коли є справедливим (6.50))

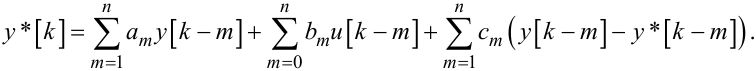(6.55)

Модель (6.55) можна записати і в дещо іншому вигляді, якщо ввести вектор-стовпець спостережень [k] та вектор-стовпець параметрів моделі , які в транспонованому варіанті мають вигляд:

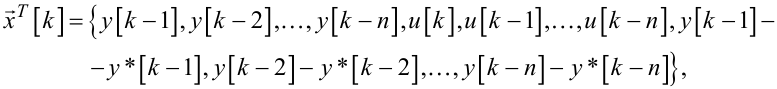(6.56)

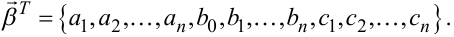(6.57)

З врахуванням виразів (6.56) та (6.57) модель (6.55) матиме вигляд:

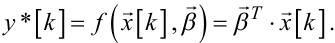(6.58)

Якщо до вектора-стовпця спостережень [k] додамо ще й значення y[k], тобто сформуємо вектор-стовпець [k], який у транспонованому варіанті матиме вигляд

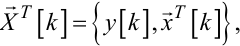(6.59)

то нев'язку (6.1) можна подати і так:

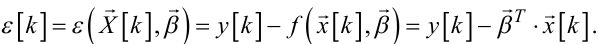(6.60)

В разі, якщо вектор параметрів моделі знайдено шляхом мінімізації критерію ідентифікації (6.41), тобто він є оптимальним вектором _O, то матимемо

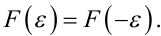(6.61)

тобто у цьому випадку нев'язка ε[k] визначатиметься виключно лише завадою ξ[k], а критерій ідентифікації (6.41) матиме найменше значення, яке дорівнюватиме дисперсії випадкової величини ξ[k], тобто

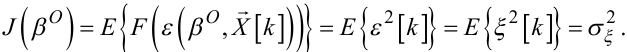(6.62)

Звертаємо увагу на те, що при отриманні (6.62) використано не лише вираз (6.61), але і (6.5).