6.4 Критерій якості ідентифікації

Як вже було зазначено раніше, за критерій якості ідентифікації будемо брати середні втрати J() , які в загальному вигляді задаються виразом (6.2), а з врахуванням (6.32) можуть розглядатись як функція (3n + 2) змінних, якими виступають складові вектора параметрів , пошук оптимальних значень яких здійснюється в процесі розв'язання задачі ідентифікації.

Як відомо з курсу математичного аналізу, щоб знайти координати точки оптимуму функції багатьох змінних, необхідно: 1) взяти від цієї функції перші частинні похідні за кожною координатою і, прирівнявши їх нулю, побудувати систему такої кількості рівнянь, скільки координат потрібно знайти; 2) розв'язати отриману систему рівнянь — її розв'язок і буде задавати координати точки оптимуму цієї функції.

А для того, щоб з'ясувати характер оптимуму — це мінімум чи максимум функції — потрібно взяти другі частинні похідні за усією сукупністю координат від цієї функції і з'ясувати, буде позитивно чи негативно визначеною матриця цих других частинних похідних в точці оптимуму, тобто чи будуть більшими від нуля всі її діагональні мінори у випадку позитивної визначеності матриці, або чи будуть меншими від нуля всі її діагональні мінори у випадку негативної визначеності матриці. При позитивній визначеності матриці других похідних функції в точці оптимуму матимемо у цій точці мінімум функції, а при негативній — максимум.

Якщо позначити вектор-стовпець перших частинних похідних від середніх втрат ∇J() розмірністю ((3n + 2),1), вектор-стовпець координат в точці оптимуму ^О розмірністю ((3n + 2),1), матрицю других частинних похідних від середніх втрат в точці оптимуму ∇²J() розмірністю ((3n + 2),(3n + 2)), вектор-стовпець перших частинних похідних від функції втрат ∇F(ε([k],)) розмірністю ((3n + 2),1), матрицю других частинних похідних від функції втрат в точці оптимуму ∇²F(ε([k],)) розмірністю ((3n + 2),(3n + 2)), а також врахувати те, що операції інтегрування (знаходження математичного очікування — символ E ) та диференціювання можна міняти місцями, то все, що сказано у перших трьох абзацах цього підрозділу для випадку мінімуму значення критерію, математично можна подати так:

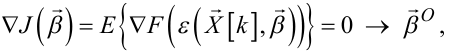(6.63)

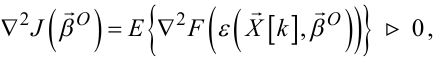(6.64)

де

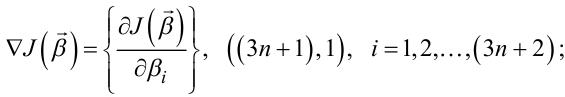(6.65)

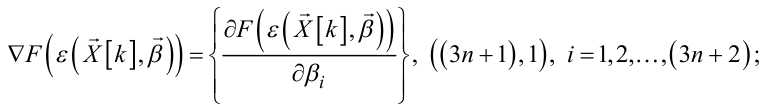(6.66)

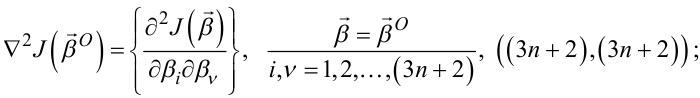(6.67)

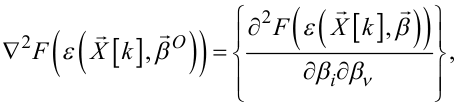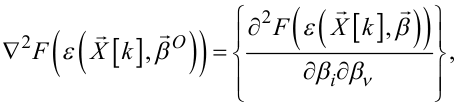(6.68)

Якщо задамось критерієм якості ідентифікації у вигляді середніх втрат J(), які є математичним очікуванням функції втрат F(ε([k],)), тобто

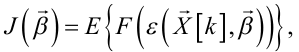(6.69)

то основою його є функція втрат F(ε), від якої вимагається лише те, щоб вона була парною функцією від нев'язки ε[k], тобто щоб для неї виконувалась умова

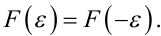(6.70)

Візьмемо функцію втрат у вигляді квадратичної функції від нев'язки, тобто нехай

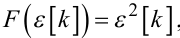(6.71)

де ε[k] задається виразом (6.60). Нехай відомо, що дисперсія нев'язки є константою

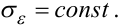(6.72)

Сформуємо функцію

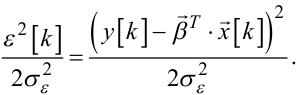(6.73)

Функція (6.73) задає параболоїд в просторі (3n + 2) координат вектора параметрів моделі з вершиною, розміщеною у тій же самій точці, в якій розміщена вершина параболоїда (6.71), але з деформацією кожного значення функції (6.71) на 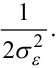. Цілком очевидно, що, беручи частинні похідні від функцій (6.71) і (6.73) за кожною складовою вектора параметрів моделі , прирівнюючи їх нулю і розв'язуючи отримані системи рівнянь, матимемо тотожні результати

А тепер давайте сформуємо функцію

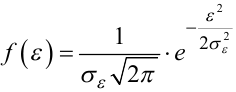(6.74)

і візьмемо від неї натуральний логарифм зі знаком «мінус». Отримаємо

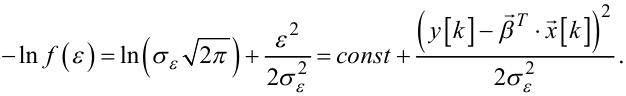(6.75)

Беручи частинні похідні від функцій (6.75) і (6.73) за кожною складовою вектора параметрів моделі , прирівнюючи їх нулю, усереднюючи і розв'язуючи отримані системи рівнянь, і в цьому випадку матимемо тотожні результати.

Тож виходить, що в разі мінімізації квадрата нев'язки за функцію втрат можна брати замість функції (6.71) функцію (6.75).

А тепер звернемо увагу на вираз (6.61), згідно з яким в разі використання оптимального вектора параметрів моделі ^О нев'язка ε[k] стає тотожною випадковому збуренню ξ[k], що діє на динамічну систему. Якщо це збурення підпорядковане нормальному закону розподілу і виконується умова (6.4), то густина його розподілу матиме вигляд

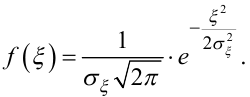(6.76)

Порівнюючи функції (6.74) і (6.76), бачимо, що вони відрізняються тільки позначенням аргументу, тобто

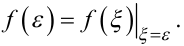(6.77)

А це, у свою чергу, означає, що за оптимальну функцію втрат F_О(ε) в критерії якості ідентифікації (6.69) в разі, якщо випадкова завада ξ підпорядкована нормальному закону розподілу з густиною f(ξ), можна використовувати функцію

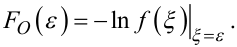(6.78)

Ми довели справедливість виразу (6.78) для випадку, коли завада, що діє на динамічну систему, підпорядкована нормальному закону розподілу. А професор Ципкін Я. З. встановив, що цей вираз є справедливим для функції втрат динамічної системи, що ідентифікується, при будь-якому розподілі її випадкового збурення.