6.5 Алгоритми ідентифікації

Згідно з постановкою задачі ідентифікації для отримання оптимальних значень усіх складових вектора параметрів моделі ⁰ необхідно розв'язати систему рівнянь (6.63), яку розв'язувати потрібно через нелінійність цих рівнянь або у випадку лінійності через велику їх кількість в системі одним із методів послідовних наближень.

Якщо структура середніх втрат (6.69) може бути заданою в явному вигляді, тобто вдалося б взяти в явному вигляді інтеграли при визначенні математичного очікування від функції втрат, то алгоритм ідентифікації, тобто алгоритм розрахунку оцінки вектора параметрів моделі динамічної системи, може бути заданим у вигляді

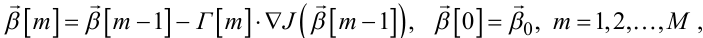(6.79)

де Г[m] — квадратна матриця розмірністю ((3n + 2),(3n + 2)), в залежності від вигляду якої алгоритм (6.79) задає той чи інший метод послідовних наближень.

Так, наприклад, якщо

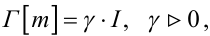(6.80)

де I — одинична матриця розмірністю ((3n + 2),(3n + 2)), то алгоритм (6.79) задає градієнтний метод послідовних наближень, а якщо

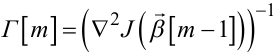(6.81)

— то метод Ньютона.

Блок-схема алгоритму ідентифікації (6.79) зображена на рис. 6.6. Вона відповідає автономній дискретній динамічній системі, в якій лінія затримки ЛЗ, що охоплена позитивним зворотним зв'язком, разом із суматором виконує функцію дискретного інтегратора (дигратора).

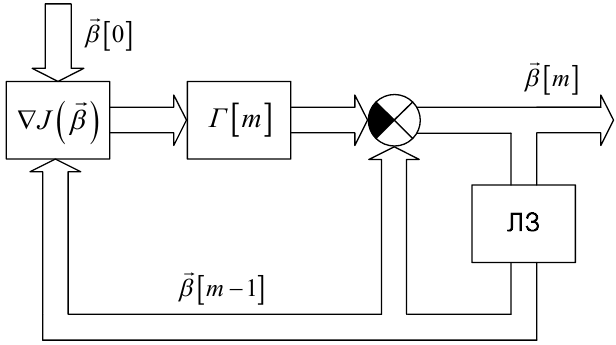
Рисунок 6.6 — Блок-схема алгоритму ідентифікації, який використовує критерій середніх втрат, заданий в явному вигляді

Якщо ж структура середніх втрат (6.69) не може бути заданою в явному вигляді, то алгоритм ідентифікації, тобто алгоритм розрахунку оцінки вектора параметрів моделі динамічної системи, необхідно задавати в іншому вигляді, а саме:

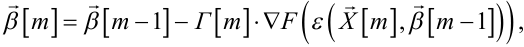(6.82)

де, знову ж таки, Г[m] — квадратна матриця розмірністю ((3n + 2),(3n + 2)), в залежності від вигляду якої алгоритм (6.82) задає той чи інший метод послідовних наближень.

Так, наприклад, якщо

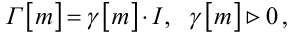(6.83)

де I — одинична матриця розмірністю ((3n + 2),(3n + 2)), то алгоритм (6.82) задає градієнтний метод стохастичної апроксимації

Блок-схема алгоритму ідентифікації (6.82) зображена на рис. 6.7. Вона відповідає не автономній дискретній динамічній системі, оскільки на вхід нелінійного перетворювача, який задає градієнт функції втрат, надходить, формуючи рекурентний режим обчислень, поточний вектор спостережень [m].

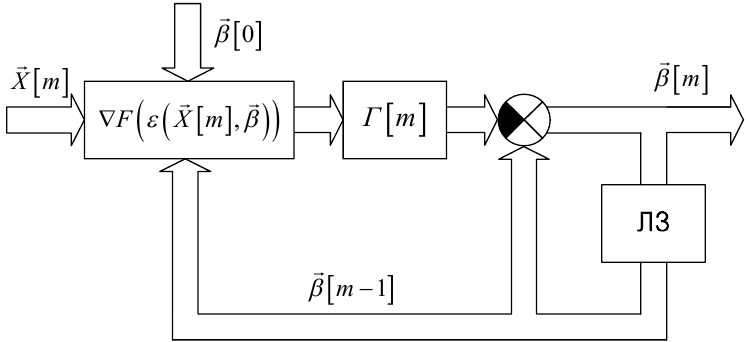
Рисунок 6.7 — Блок-схема алгоритму ідентифікації, який використовує функцію втрат

Ми не будемо зупинятись на питаннях збіжності алгоритмів ідентифікації, а відзначимо лише те, що при гладких функціях втрат і випуклих функціях середніх втрат в задачах ідентифікації стійких динамічних систем наведені вище алгоритми є збіжними, тобто з ростом числа ітерацій m оцінка вектора [m] наближається до його оптимального значення ^О . Реально ж зупиняємо процес ітерацій тоді, коли оцінка перестає змінюватись у тому розряді значень після коми, який влаштовує за точністю обчислень.