7.2 Рівняння математичної фізики як моделі елементів систем з розподіленими параметрами

Почнемо з побудови математичної моделі довгої лінії електропередачі ЛЕП (рис. 7.1), за допомогою якої електроенергія від генератора Г електростанції з електрорушійною силою E через підвищувальний трансформатор ПТ з приведеним повним опором Z^П та знижувальний трансформатор Т з приведеним повним опором Z^T передається до навантаження Н з повним опором Z^H.

Об'єднаємо опір Z^T знижувального трансформатора Т з опором Z^H навантаження в сумарний опір Z^K, підключений до кінця лінії електропередачі.

Тоді функціональну схему (рис. 7.1) можна замінити принциповою схемою, наведеною на рис. 7.2, на якій довга лінія електропередачі ЛЕП подається як послідовний ланцюг Г-подібних чотириполюсників з параметрами R_j, L_j, G_j, C_j (на рис. 7.2 показано лише один з них: j -ий), де R_j — питомий активний опір j-ої ділянки фази ЛЕП, а L_j, G_j, C_j — відповідно, питома індуктивність, питома активна провідність і питома ємність цієї ділянки.

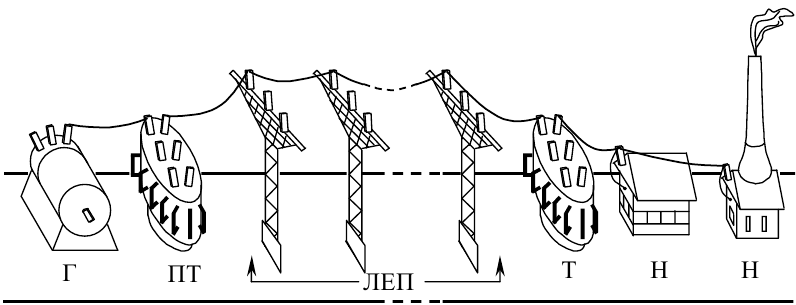
Рисунок 7.1 — Функціональна схема однієї фази електричної системи, до складу якої входить генератор Г електростанції, підвищувальний трансформатор ПТ, довга лінія електропередачі ЛЕП, знижувальний трансформатор Т та навантаження Н

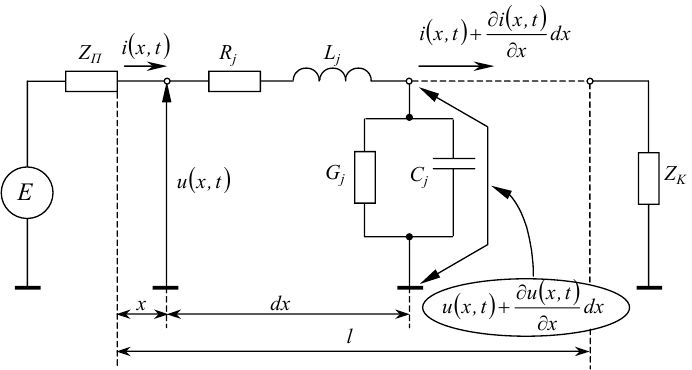
Рисунок 7.2 — Принципова схема однієї фази електричної системи

Позначимо u(x,t), i(x,t), відповідно, напругу і струм на вході j-го елемента схеми фази ЛЕП. Тоді на виході j-го елемента довжиною dx матимемо напругу і струм, що дорівнюють:

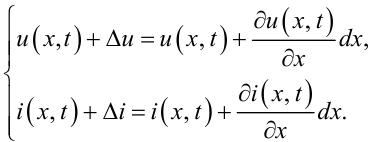(7.1)

Запишемо перший та другий закони Кірхгофа для j-го елемента схеми фази ЛЕП, опускаючи у першому законі диференціали 2-го порядку, які є нескінченно малими величинами 2-го порядку малості. Матимемо:

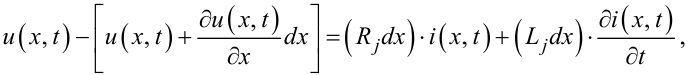(7.2)

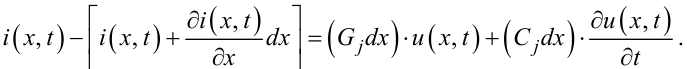(7.3)

Розкриваючи квадратні дужки в лівій частині рівнянь (7.2), (7.3) і ділячи ці рівняння на dx, отримаємо:

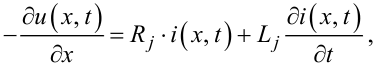(7.4)

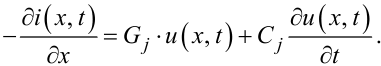(7.5)

Приймаючи умову, що параметри R_j, L_j, G_j, C_j є величинами сталими і однаковими для всіх ділянок схеми фази ЛЕП, рівняння (7.4), (7.5) можна записати так:

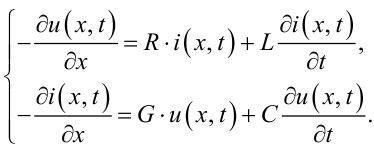(7.6)

Диференціальні рівняння (7.6) в частинних похідних і задають математичну модель довгої лінії електропередачі. Для отримання їх однозначного розв'язку необхідно задати початкові i(x, 0), u(x, 0), та граничні i(0, 0), u(0, 0) або i(l,t_k), u(l,t_k) умови.

Замість системи двох диференціальних рівнянь в частинних похідних 1-го порядку (7.6) відносно функцій u(x,t), i(x,t) як модель довгої ЛЕП можна використовувати і одне диференціальне рівняння в частинних похідних 2-го порядку відносно лише однієї функції u(x,t)

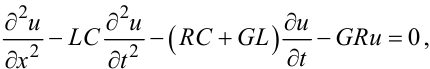(7.7)

або лише однієї функції i(x,t):

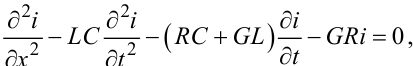(7.8)

які легко отримати із рівняння (7.6) шляхом додаткового диференціювання і підстановки одного рівняння в інше.

Покажемо це на прикладі отримання рівняння (7.8).

Перший крок: продиференціюємо за x друге рівняння системи (7.6), в результаті чого отримаємо:

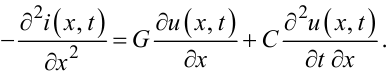(7.9)

Другий крок: підставимо замість першого члена в правій частині рівняння (7.9) його значення із першого рівняння системи (7.6), в результаті чого отримаємо:

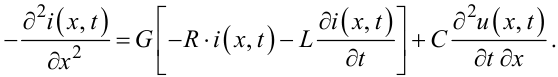(7.10)

Третій крок: продиференціюємо перше рівняння системи (7.6) за t, в результаті чого отримаємо:

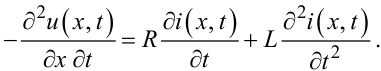(7.11)

Четвертий крок: пам'ятаючи про те, що при незалежних змінних черговість диференціювання функції від них для отримання змішаної частинної похідної 2-го порядку ролі не грає, підставимо замість останнього члена в правій частині рівняння (7.10) його значення з рівняння (7.11), в результаті чого отримаємо:

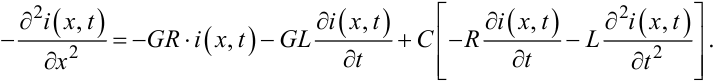(7.12)

П'ятий крок: переносимо усі члени рівняння (7.12) в одну сторону і зводимо подібні члени, в результаті чого отримаємо рівняння (7.8).

Аналогічним способом шляхом вилучення функції i(x,t) та її похідних із системи (7.6) виводиться і рівняння (7.7).

Легко бачити, що обидва вони мають однакову структуру.

В теорії диференціальних рівнянь в частинних похідних рівняння (7.7), (7.8) відносять до рівнянь математичної фізики гіперболічного типу. З цих рівнянь шляхом прирівнювання до нуля окремих параметрів можна отримати математичні моделі трубопровідних ліній і тросів.

Очевидно, що в трубопроводах витік газу чи рідини через стінку відсутній, тому для них справедливою буде умова

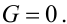(7.13)

З фізики відомо, що для гідравлічних і пневматичних систем аналогом електричної напруги u(x,t) є тиск p(x,t), а аналогом електричного струму i(x,t) є об'ємна витрата Q(x,t), тобто для трубопроводів є справедливим

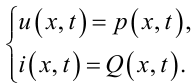(7.14)

З врахуванням умов (7.13), (7.14) з (7.7), (7.8) знайдемо, що математичні моделі гідравлічних або пневматичних трубопроводів мають вигляд:

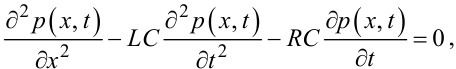(7.15)

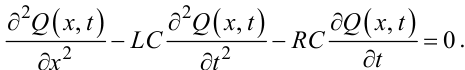(7.16)

В рівняннях (7.15), (7.16):

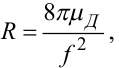(7.17)

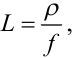(7.18)

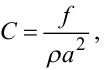(7.19)

де f — площа поперечного перерізу труби, μ_Д — динамічний коефіцієнт в'язкості газу чи рідини, ρ — густина газу чи рідини, a — швидкість розповсюдження звуку в газі чи рідині.

Рівняння (7.15), (7.16) залишаються в класі гіперболічних рівнянь математичної фізики.

Якщо цікавить передача тепла вздовж довгого ізольованого стержня, то, враховуючи умови

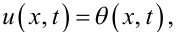(7.20)

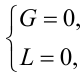(7.21)

для опису процесу зміни температури θ(x,t) в часі і вздовж стержня, з рівняння (7.7) отримаємо модель:

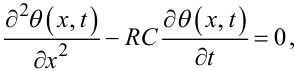(7.22)

яку називають рівнянням теплопровідності і відносять до класу параболічних рівнянь математичної фізики.

В рівнянні (7.22)

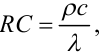(7.23)

де ρ — густина матеріалу стержня, c — питома теплоємність цього матеріалу, а λ — коефіцієнт його теплопровідності.

Аналогічну модель за умови (7.21) та умови

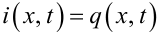(7.24)

із рівняння (7.8) можна отримати для опису процесу розповсюдження теплового потоку q(x,t) в часі та вздовж стержня, а саме:

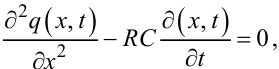(7.25)

для якої є також справедливою умова (7.23).

Слід зазначити, що рівняннями параболічного типу описуються також процеси передачі низькочастотних сигналів в телеграфних і телефонних кабелях, для яких в достатньому для практичних розрахунків наближенні виконується умова (7.21).

Тож процес розповсюдження напруги u(x,t) в такому кабелі досить точно описується рівнянням

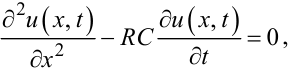(7.26)

а процес розповсюдження струму — рівнянням

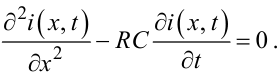(7.27)

З теорії подібності відомо, що аналогом електричної напруги u(x,t) для механічних систем є швидкість руху тіла v(x,t), аналогом електричного струму i(x,t) є сила F(x,t), яка діє на тіло, а аналогами індуктивності L, активного опору R та ємності C, відповідно, є податливість n, механічна провідність тертя h та маса m.

Виходячи з указаних аналогій, а також з того, що для тросів, як і для трубопроводів, справедливою є умова (7.13), із рівнянь (7.7), (7.8) можна записати математичні моделі для троса у вигляді:

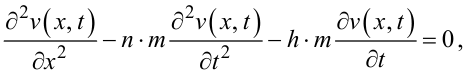(7.28)

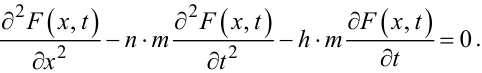(7.29)

Ці моделі суттєво спрощуються, не вносячи суттєвих похибок, якщо не враховувати механічну провідність тертя в тросі, тобто за умови, що

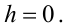(7.30)

У цьому випадку з рівнянь (7.28), (7.29) матимемо:

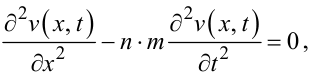(7.31)

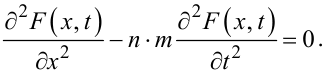(7.32)

Рівняння (7.31), (7.32) в математичній фізиці носять назву рівнянь коливання струни.

Завершимо розгляд математичних моделей об'єктів з розподіленими параметрами моделлю широко розповсюдженого теплообмінника типу «труба в трубі» (рис. 7.3).

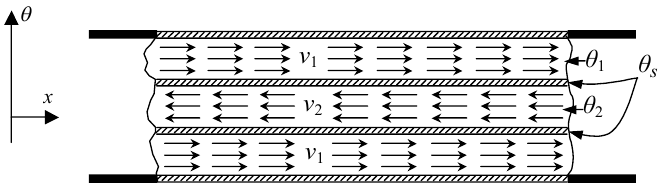
Рисунок 7.3 — Повздовжній розріз секції теплообмінника типу «труба в трубі»

Цю модель запишемо лише для процесу зміни в часі та вздовж труби температури в рідких середовищах θ₁, θ₂ та у стінці θ_s, що їх розділяє.

При розробці цієї моделі використано дуже розповсюджений і практично підтверджений принцип, що швидкість зміни температури θ рідини, що переміщується зі швидкістю v в часі та вздовж труби, яка характеризується відповідними похідними, пропорційна різниці температур цієї рідини та стінки, від якої надходить потік тепла, тобто

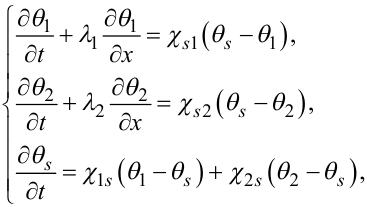(7.33)

де θ₁ — температура рідини в зовнішній трубі, θ₂ — температура рідини у внутрішній трубі, θ_s — температура тонкої стінки внутрішньої труби, яка розділяє рідини, χ_s1, χ_s2, χ_1s, χ_2s — коефіцієнти теплопровідності між стінкою внутрішньої труби і рідинами, λ₁, λ₂ — коефіцієнти, які характеризують режими роботи теплообмінника і визначаються через швидкість рідин, тобто:

• в режимі току (коли обидві рідини рухаються по трубах в одному напрямку):

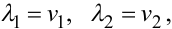(7.34)

• в режимі протитоку (коли обидві рідини рухаються по трубах назустріч одна одній):

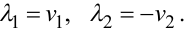(7.35)

Моделлю (7.33) і завершимо розгляд моделей елементів систем з розподіленими параметрами, що базуються на рівняннях математичної фізики.

Очевидно, що у випадках, коли необхідно проаналізувати лише процеси, які протікають в конкретних об'єктах з розподіленими параметрами, достатньо задати початкові та граничні умови і розв'язати відповідні рівняння математичної фізики, що описують процеси в цих об'єктах. Якщо ж об'єкт з розподіленими параметрами є складовою ланкою системи, то аналіз процесу в ньому буде не таким простим.