7.3 Аналіз математичних моделей систем з розподіленими параметрами

В найбільш загальному вигляді математична модель об'єкта з розподіленими параметрами на основі диференціальних рівнянь в частинних похідних отримана у вигляді (7.6)

Як показано в попередньому підрозділі, із системи рівнянь (7.6) можна отримати всі інші важливі для практики моделі об'єктів з розподіленими параметрами як в класі диференціальних рівнянь математичної фізики гіперболічного типу, так і параболічного.

Тож немає потреби аналізувати всі отримані в попередньому підрозділі моделі. Достатньо провести аналіз найбільш загальної моделі у вигляді (7.6) і показати як розповсюдити отримані результати на всі інші випадки.

Вважаючи початкові умови нульовими, перетворимо за Лапласом рівняння системи (7.6), вважаючи незалежною змінною час t , а x розглядаючи як параметр. В результаті перетворення отримаємо:

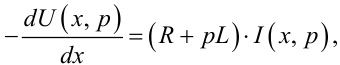(7.36)

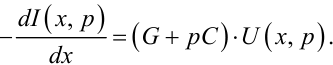(7.37)

Звертаємо увагу, що після перетворення за Лапласом, тобто взяття інтегралів Лапласа за змінною t, функції U(x,p), I(x,p) стають функціями лише однієї незалежної змінної x з параметром p, тож в рівняннях (7.36), (7.37) маємо право розглядати не частинні похідні від функцій, як було в (7.6), а звичайні.

Продиференціювавши за x рівняння (7.36), отримаємо:

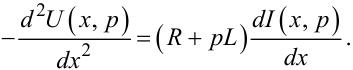(7.38)

Підставивши в рівняння (7.38) значення похідної струму з рівняння (7.37) і перенісши всі члени в одну сторону, матимемо:

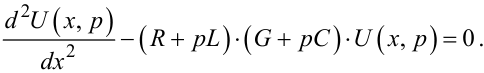(7.39)

Рівняння (7.39) є диференціальним рівнянням 2-го порядку відносно U(x,p) за змінною x, характеристичне рівняння якого має вигляд:

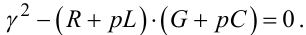(7.40)

Коренями рівняння (7.40), очевидно, є

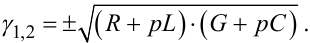(7.41)

Зауважимо, що корінь γ₁, як правило, називають коефіцієнтом розповсюдження хвилі, або хвилевою сталою, і позначають як

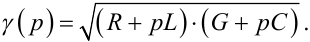(7.42)

Введення (7.42) дає нам право стверджувати, що

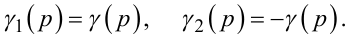(7.43)

З теорії диференціальних рівнянь відомо, що загальний розв'язок диференціального рівняння 2-го порядку (7.39) можна записати у вигляді:

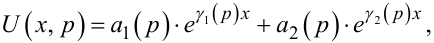(7.44)

або, враховуючи (7.42), (7.3), у вигляді:

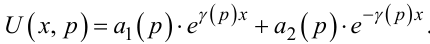(7.45)

Для визначення a₁(p), a₂(p) використаємо граничні умови, які, як видно з рис. 7.2, мають вигляд:

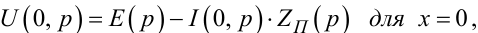(7.46)

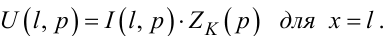(7.47)

Підставляючи x = 0 в рівняння (7.44), отримаємо:

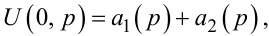(7.48)

або, з врахуванням (7.46):

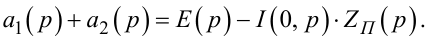(7.49)

Продиференціювавши (7.45) за x, отримаємо:

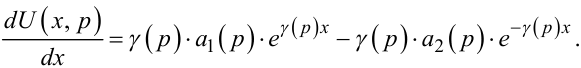(7.50)

Зіставлення рівнянь (7.36) та (7.50) дає нам право записати, що

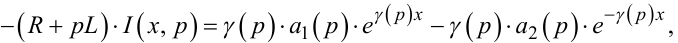(7.51)

або

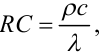(7.52)

При x = 0 з рівняння (7.52) матимемо:

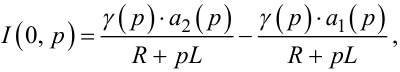(7.53)

При x = l із рівняння (7.52) матимемо:

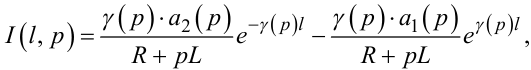(7.54)

а з рівняння (7.45):

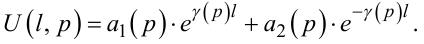(7.55)

Підставляючи (7.53) в (7.49), а (7.54) і (7.55) в (7.47), отримаємо два рівняння з двома невідомими a₁(p), a₂(p), а саме:

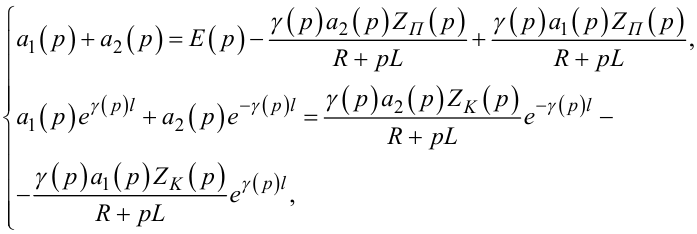(7.56)

або

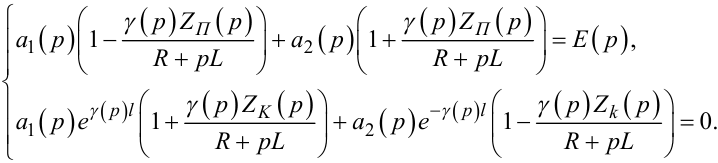(7.57)

Розв'язуючи систему рівнянь (7.57), знайдемо, що

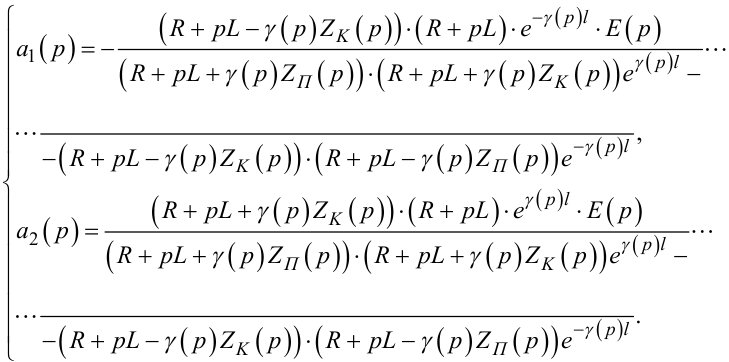(7.58)

Нехай

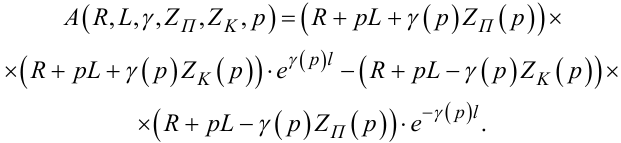(7.59)

Підставляючи значення a₁(p), a₂(p) із (7.58) у (7.45) з врахуванням (7.59), отримаємо:

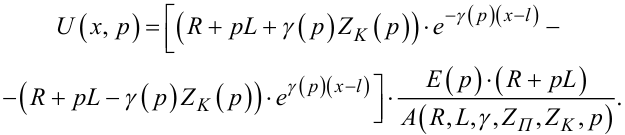(7.60)

Оскільки передаточна функція об'єкта W(x, p) — це відношення перетворених за Лапласом вихідного сигналу U(x, p) до вхідного E(p), то

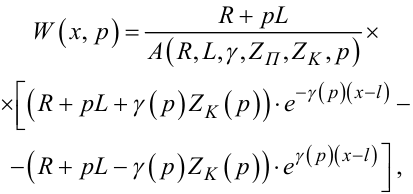(7.61)

а рівняння (7.60) можна записати і так:

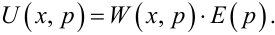(7.62)

Якщо довга лінія є об'єктом управління, а тому цікавими є процеси, що в ній протікають, як у часі, так і в просторі, тобто вздовж обох координат t, x, то в структурній схемі такої системи цю лінію слід враховувати передаточною функцією (7.61).

Якщо ж довга лінія є елементом зв'язку між регулятором та об'єктом управління, то не будемо цікавитись процесами, які протікають у самій лінії вздовж координати x , а цікавитимось лише передавальними властивостями лінії, і тому у структурній схемі її слід враховувати передаточною функцією W(x, p), яку отримаємо із (7.61) підстановкою x = l, тобто функцією

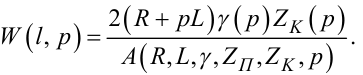(7.63)

Для трубопроводів структура передаточних функцій (7.61), (7.63) зберігається, але в зв'язку з виконанням для них умови (7.13) змінюється вираз, за допомогою якого визначається параметр γ(p), тобто замість (7.42) будемо використовувати

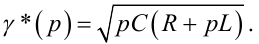(7.64)

А для процесу передачі тепла в довгому ізольованому середовищі у зв'язку з виконанням умови (7.21) змінюється як параметр γ(p), тобто замість (7.42) слід використовувати

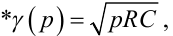(7.65)

так і структура передаточних функцій (7.61), (7.63), тобто замість них слід використовувати

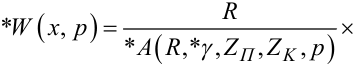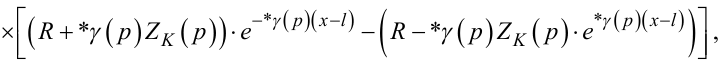(7.66)

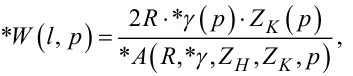(7.67)

де

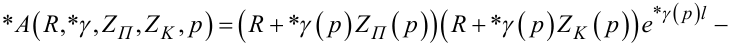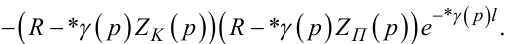(7.68)

Нагадаємо, що рівнянням математичної фізики параболічного типу описується не лише процес передачі тепла, а й процес передачі низькочастотних сигналів в телефонних і телеграфних лініях. А тому для передаточних функцій телефонних і телеграфних довгих ліній теж будуть справедливими співвідношення (7.65) – (7.68).

Ще більш простими є вирази для γ(p), W(x, p), W(l, p), за допомогою яких в системах управління описуються троси, оскільки для них виконується не лише умова (7.13), але й умова (7.30). Для тросів замість (7.42), (7.61) та (7.63) матимемо:

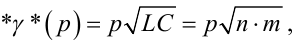(7.69)

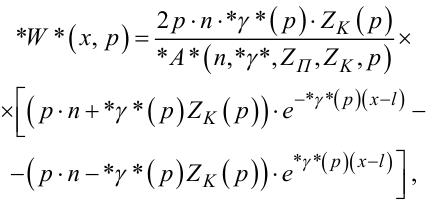(7.70)

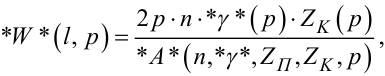(7.71)

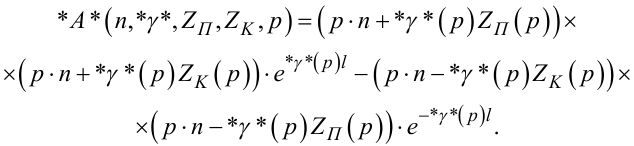(7.72)

Тепер розглянемо більш детально модель теплообмінника «труба в трубі» (7.33).

Перетворюючи за Лапласом третє рівняння системи (7.33), отримаємо:

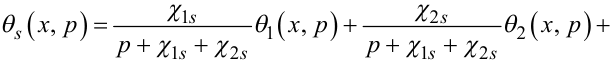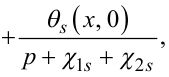(7.73)

де

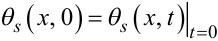(7.74)

початкова умова вздовж стінки, що розділяє рідини з температурами θ₁ і θ₂.

Аналогічно, перетворюючи за Лапласом перше і друге рівняння системи (7.33), матимемо:

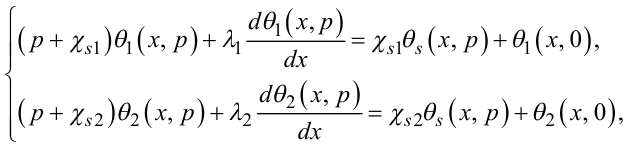(7.75)

де

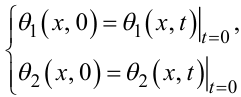(7.76)

— початкові умови для температури в обох рідинах вздовж труби.

Підставляючи в рівняння (7.75) значення θ_s(x, p) із (7.73), отримаємо:

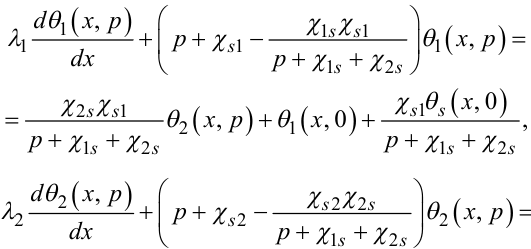(7.77)

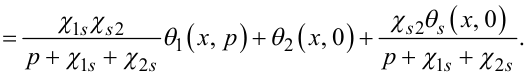(7.78)

Перетворюючи рівняння (7.77), (7.78) за Лапласом за просторовою координатою x, матимемо:

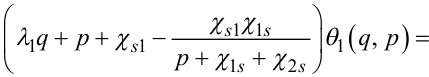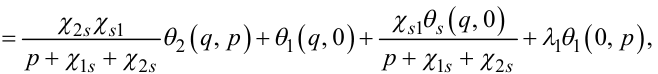(7.79)

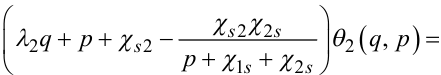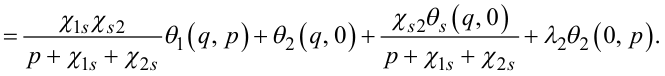(7.80)

Позначимо:

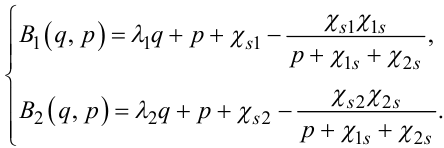(7.81)

З врахуванням (7.81), рівняння (7.79), (7.80) можна переписати так:

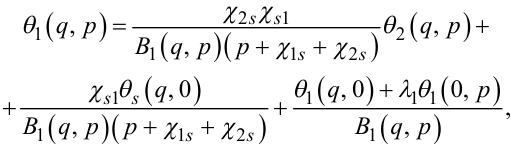(7.82)

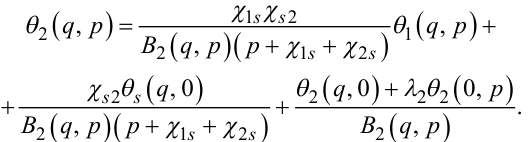(7.83)

Підставляючи рівняння (7.82) в (7.83), отримаємо рівняння відносно θ₂(q, p) та початкових θ₁(q, 0), θ_s(q, 0), θ₂(q, 0) і граничних θ₁(0, p), θ₂(q, p) умов, розв'язуючи яке отримаємо двовимірне зображення за Лапласом моделі температурного процесу 2 q, p , застосовуючи до нього двовимірне обернене перетворення за Лапласом, знайдемо θ₂(x, t).

За аналогією, підставляючи рівняння (7.83) у (7.82) і застосовуючи наведений вище алгоритм, знайдемо θ₁(x, t).

Слід зазначити, що якщо теплообмінник є елементом якоїсь замкнутої системи керування, то в структуру цієї системи він увійде структурною схемою, наведеною на рис. 7.4.

Оскільки передаточні функції окремих ланок на цій схемі легко визначаються її зіставленням з рівняннями (7.82), (7.83), то окремо виписувати їх не будемо.

Але, як і в кінці попереднього підрозділу, ще раз наголошуємо на тому, що структурною схемою, наведеною на рис. 7.4, з відповідно визначеними двовимірними передаточними функціями, теплообмінник «труба в трубі» слід задавати лише у випадках, коли він є складовою ланкою більш складної системи, наприклад, системи автоматичного керування, і процеси в ньому цікавитимуть у взаємозв'язку з процесами в інших складових ланках цієї системи.

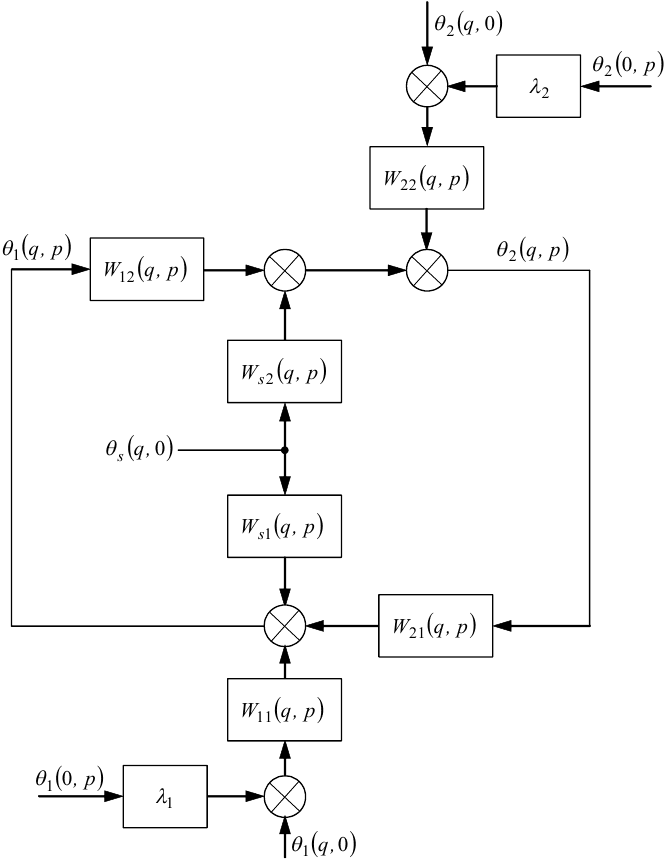
Рисунок 7.4 — Структурна схема теплообмінника «труба в трубі»

Якщо ж викликають цікавість лише процеси, що протікають в теплообміннику, який розглядається сам по собі, то простіше такий аналіз здійснювати шляхом безпосереднього розв'язання рівнянь (7.33) чисельними методами за допомогою комп'ютерів, оснащених пакетами Mathcad чи Matlab.