7.4 Математичні моделі систем з чистим запізненням

В класі систем з розподіленими параметрами особливе місце займають системи з чистим запізненням.

Це, наприклад, технологічні об'єкти з переміщенням матеріалів за допомогою конвеєрів, пристрої з лініями затримки сигналу чи хімічні реактори з конвеєрним або лопатевим переміщенням реагентів.

Їх особливе місце пояснюється тим, що після визначення чистого запізнення проходження сигналу в таких об'єктах процеси в них можна описувати за допомогою звичайних диференціальних рівнянь, а не рівнянь в частинних похідних, що значно простіше.

Почнемо розгляд моделей об'єктів з чистим запізненням з найпростішого з них — лінії затримки (ЛЗ) сигналу (рис. 7.5).

     
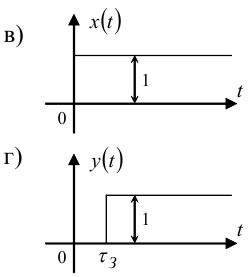
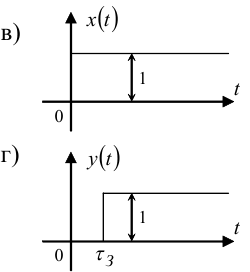
Рисунок 7.5 — Функціональна і структурна схеми лінії затримки та графіки її вхідного x(t) і вихідного y(t) сигналів

Як видно з рис. 7.5, в та рис. 7.5, г, ЛЗ лише затримує проходження вхідного сигналу, не змінюючи його форми.

Знайдемо передаточну функцію ЛЗ.

За визначенням вона дорівнює відношенню перетворених за Лапласом вихідного та вхідного сигналів. Тож

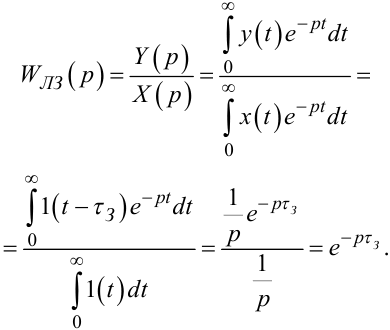(7.84)

Якщо згадати, що АФЧХ об'єкта — це

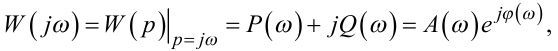(7.85)

де P(ω), Q(ω), A(ω), φ(ω) — відповідно, дійсна, уявна, амплітудна та фазова частотні характеристики, то із (7.84), (7.85) випливає, що:

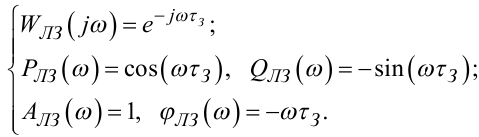(7.86)

На рис. 7.6 наведені усі частотні характеристики ЛЗ, що визначаються співвідношеннями (7.86), які є її математичними моделями в частотній області.

Рисунок 7.6 — Частотні характеристики лінії затримки сигналу

Очевидно, що всі моделі, визначені для лінії затримки сигналу, будуть справедливими і для конвеєрних ліній з тією лише різницею, що характеристики W(p), W(jω), P(ω), Q(ω) і A(ω) будуть мати множником коефіцієнт передачі kK , який буде меншим одиниці в разі, якщо частина матеріалу, що насипається на конвеєр на його вході, просипаючись, не доходить до його кінця, тобто для конвеєра

(7.87)

Перейдемо до розгляду хімічних реакторів.

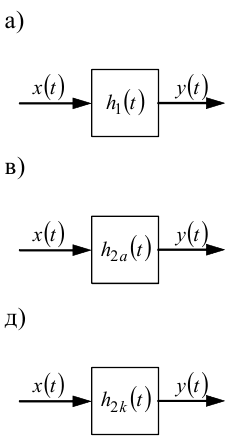
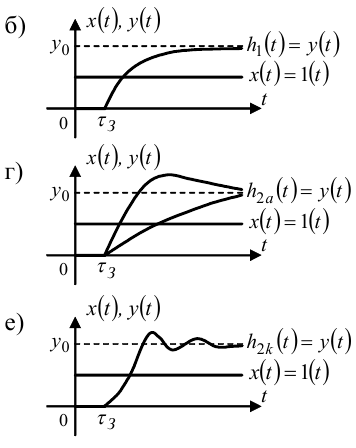
Рисунок 7.7 — Можливі варіанти перехідних характеристик хімічних реакторів

На рис. 7.7 наведені можливі варіанти перехідних характеристик хімічних реакторів h₁(t), h_2a(t), h_2k(t), які є їх реакціями на одиничний вхідний сигнал 1(t).

Криві h₁(t), h_2a(t), h_2k(t) в першому наближенні можна описати рівняннями:

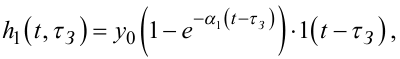(7.88)

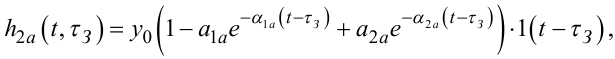(7.89)

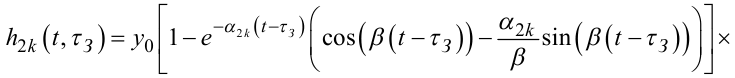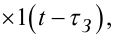(7.90)

в яких t — незалежна змінна (час), τ_З — числовий параметр, який характе- ризує запізнення реакції об'єкта на вхідний сигнал, y₀, a_1a, a_2a, a₁, a_1a, a_1a, a_1k, β — числові коефіцієнти.

Зазначимо, що одиничні функції 1(t -τ_З), що дописані як множники в рівняння (7.88) – (7.90), необхідні в структурі цих рівнянь для того, щоб формально «обнуляти» функції h₁(t,τ_З), h_2a(t,τ_З), h_2k(t,τ_З) при значеннях аргументу t, менших τ_З. Автори посібників і монографій з інженерною освітою, до речі, про це часто забувають.

Формально, функції (7.88) – (7.90) є розв'язками диференціальних рівнянь, відповідно:

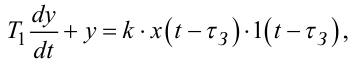(7.91)

при

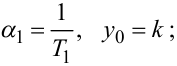(7.92)

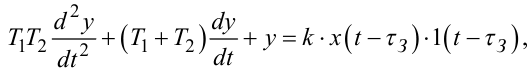(7.93)

при

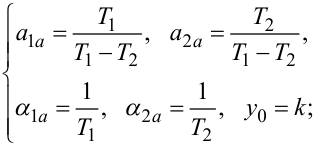(7.94)

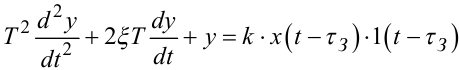(7.95)

при

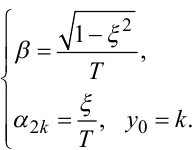(7.96)

Подаючи на вхід хімічного реактора вхідний сигнал x(t) у вигляді одиничного стрибка l(t) і фіксуючи за допомогою самописця реакцію y(t) цього хімічного реактора, отримаємо графік його перехідної характеристики h(t - τ_З), з якого одразу ж визначаються параметри τ_З та y₀.

Підставляючи ці параметри τ_З та y₀ в рівняння (7.88), якщо графік отриманої експериментально перехідної характеристики h₁(t - τ_З) має вигляд, наведений на рис. 7.7, б, отримаємо рівняння з одним невідомим α₁, для розв'язання якого відносно α₁ достатньо на графіку характеристики h₁(t - τ_З) взяти лише одну точку і підставити її координати t^*, h₁(t^* - τ_З) в рівняння (7.88). Підставивши знайдені значення α₁ і y₀ в співвідношення (7.92), визначимо коефіцієнти моделі (7.91), чим завершимо її ідентифікацію.

Якщо графік експериментально отриманої перехідної характеристики h_2a(tτ_З), має вигляд, наведений на рис. 7.7, г, то для отримання чотирьох параметрів a_1a, a_2a, a_1a, a_2a, які однозначно визначаються згідно зі співвідношеннями (7.94) лише через два параметри T₁, T₂, необхідно спочатку підставити співвідношення (7.94) в рівняння (7.89), а потім взяти дві точки на графіку характеристики h_2a(tτ_З) і, підставивши їх координати t^*, h₁(t^* τ_З) та t^**, h₁(t^** τ_З) в рівняння (7.89), побудувати систему двох рівнянь з двома невідомими T₁, T₂. Розв'язуючи цю систему двох рівнянь, знайдемо числові значення T₁, T₂, підставляючи які в модель (7.93), здійснимо її ідентифікацію.

Якщо ж графік експериментально отриманої перехідної характеристики h_2k(t^* τ_З) має вигляд, наведений на рис. 7.7, е, то для отримання двох невідомих параметрів α_2k, β необхідно взяти дві точки на графіку характеристики h_2k(t^* τ_З) і, підставивши їх координати t^*, h_2k(t^* τ_З) та t^**, h_2k(t^** τ_З) в рівняння (7.90), побудувати систему двох рівнянь з двома невідомими α_2k, β, розв'язавши яку, знайти числові значення цих невідомих. Підставивши ці числові значення в рівняння (7.96) і розв'язавши їх, знайдемо числові значення параметрів T, ξ, підставивши які разом з коефіцієнтом k в модель (7.95), здійснимо її ідентифікацію.

Два важливих зауваження:

1. В книгах, присвячених аналізу систем з розподіленими параметрами, обов'язково фігурують графічні або графоаналітичні методи визначення коефіцієнтів моделей (7.91), (7.93), (7.95). Ці методи вирішено не розглядати, оскільки в еру комп'ютерів та пакетів прикладних програм типу Mathcad чи Matlab, за допомогою яких рівняння 2-го порядку з будь-якими коефіцієнтами розв'язуються дуже просто і швидко, на наш погляд, недоцільно «засмічувати» матеріал викладенням методів, розроблених в іншу епоху і розрахованих на ручні розрахунки.

2. В околі точки стаціонарного режиму автоматичної системи в разі використання елемента з розподіленими параметрами типу хімічного реактора як об'єкт регулювання, в силу недопущення регулятором значних відхилень режиму у цій системі від стаціонарного, структуру такого об'єкта регулювання з достатнім для практичних задач ступенем адекватності можна подати у вигляді послідовного з'єднання ланки чистого запізнення і структурної ланки з передаточною функцією W_i(p), i = 1, 2, 3 не вище другого порядку (рис. 7.8), де

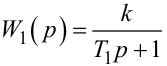(7.97)

— в разі, якщо перехідна характеристика має вигляд, наведений на рис. 7.7, б;

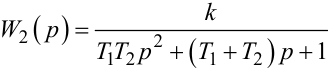(7.98)

в разі, якщо h(t, τ_З) має вигляд, наведений на рис. 7.7, г, і

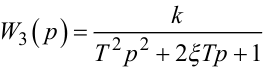(7.99)

— в разі, якщо h(t, τ_З) має вигляд, наведений на рис. 7.7, е.

В наведеному вище легко переконатись, якщо перетворити за Лапласом рівняння (7.91), (7.93), (7.95) і знайти відношення перетвореного за Лапласом вихідного сигналу Y(p) до вхідного X(p).

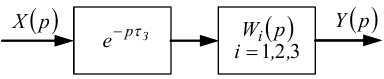
Рисунок 7.8 — Структурна схема об'єкта з розподіленими параметрами типу хімічного реактора як складової ланки системи автоматичного регулювання процесів в ньому

Виникає запитання: «А що ж робити, якщо процес в об'єкті з розподіленими параметрами типу хімічного реактора необхідно дослідити в усьому діапазоні можливих змін вхідного сигналу x(t)?».

Адже у цьому випадку використання наближених моделей у вигляді звичайних диференціальних рівнянь не вище 2-го порядку з аргументом, що запізнюється, типу (7.91), (7.93), (7.95) може призвести до суттєвих похибок.

Більш точну ідентифікацію процесів в таких об'єктах можна здійснити, використовуючи їх модель у формі імпульсної перехідної характеристики g(t), заданої у просторі ортонормованих функцій {φ_i(t)}, i = 0,1,.., n, тобто у вигляді

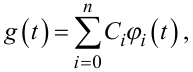(7.100)

де φ_i(t), i = 0,1, 2,..., n — функції, для яких виконуються умови ортогональності

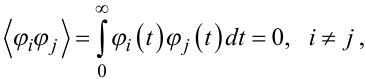(7.101)

або

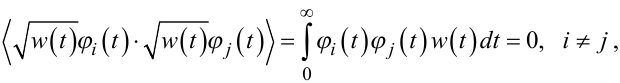(7.102)

якщо вони ортогональні з вагою , а також умови нормування

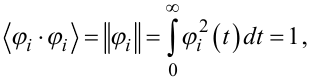(7.103)

або

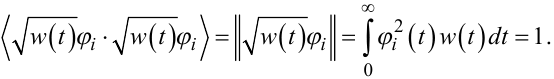(7.104)

Найпростішою і добре відомою студентам технічних університетів системою ортогональних функцій є система cos(kωt), sin(kωt), k = 1, 2,..., в якій (7.100) є розкладом функції g(t) в тригонометричний ряд Фур'є.

Більш складними системами ортогональних функцій є поліноми Ерміта, Ляггера, Чебишова, зі способом отримання яких за методикою Грама-Шмідта можна ознайомитись в будь-якому підручнику з функціонального аналізу.

На рис. 7.9 показана схема ідентифікації імпульсної перехідної характеристики g(t) в просторі ортогональних функцій {φ_i(t)}, i = 0,1,.., n.

На цій схемі , i = 0,1,..., n — коефіцієнти розкладу (проекції) функції g(t) в просторі {φ_i(t)}, i = 0,1,.., n;

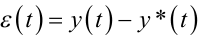(7.105)

похибка апроксимації функції g(t) ортогональним рядом (7.100);

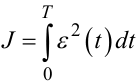(7.106)

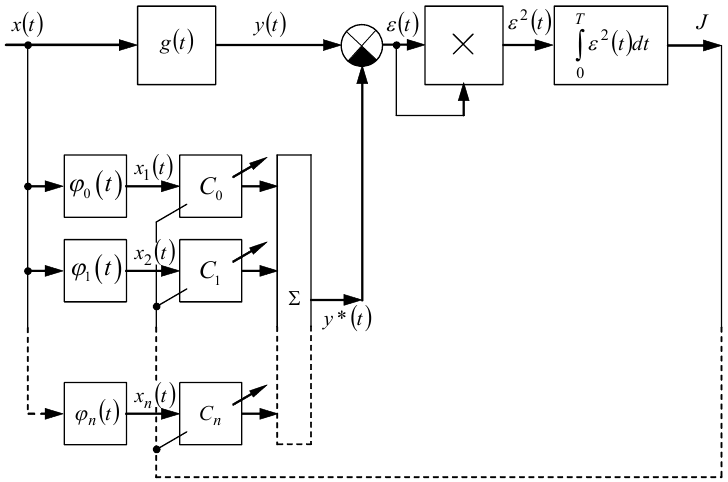
Рисунок 7.9 — Схема ідентифікації імпульсної перехідної характеристики g(t) динамічного об'єкта в просторі ортогональних функцій {φ_i(t)}, i = 0,1,.., n

Ідентифікація імпульсної перехідної характеристики g(t) ортогональним рядом (7.100) зводиться до такого налаштування коефіцієнтів C₀, C₁,..., C_n (рис. 7.9), яке приводить до мінімального значення критерію адекватності (7.106).

Маючи значення g(t), завжди можна, перетворивши її за Лапласом, отримати передаточну функцію W(p) об'єкта.

Ідентифікацію у такий спосіб можна здійснювати в процесі нормальної експлуатації об'єкта, але в цьому випадку структурна схема об'єкта не може бути показана у вигляді, зображеному на рис. 7.8, тобто вона не містить в собі ланку запізнення в чистому вигляді.

Але за допомогою аналогової ЕОМ можна здійснити ідентифікацію об'єкта з розподіленими параметрами так, що і ланка чистого запізнення в його структурній схемі зберігається, і коефіцієнти диференціального рівняння високого порядку, які є одночасно і коефіцієнтами передаточної функції, визначаються в процесі нормальної експлуатації цього об'єкта.

В загальному вигляді схема цього способу ідентифікації показана на рис. 7.10, на якому модель об'єкта задається диференціальним рівнянням з аргументом, що запізнюється (ДРАЗ), а критерій адекватності моделі має той же вигляд, що і в попередньому випадку, тобто визначається функціоналом (7.106).

Рисунок 7.10 — Схема ідентифікації об'єкта з розподіленими параметрами за допомогою моделі у вигляді диференціального рівняння з аргументом, що запізнюється (ДРАЗ)

Для розкриття суті цього способу ідентифікації припустимо, що процес в об'єкті реально описується диференціальним рівнянням

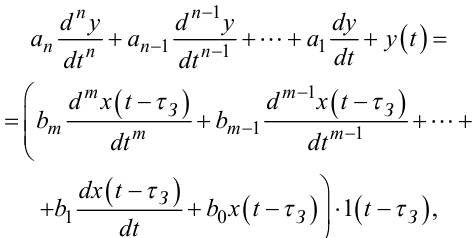(7.107)

коефіцієнти якого і значення чистого запізнення τ_З не знаємо, а знаємо лише показники n та m

Позначимо оператор диференціювання символом D. Тоді матимемо:

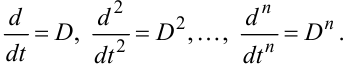(7.108)

Запізнення аргументу в усіх членах правої частини на τ_З можна подати як дію оператора e^-Dτ_З на відповідну функцію, тобто

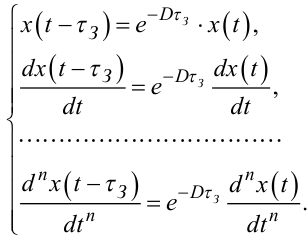(7.109)

З врахуванням співвідношень (7.108), (7.109) ДРАЗ (7.107) можна переписати так:

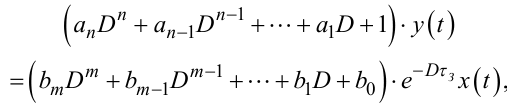(7.110)

або

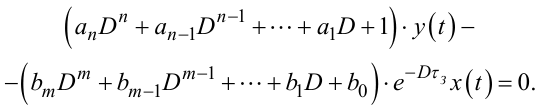(7.111)

Нехай є можливість вхідний сигнал x(t) подати на аналогову ЕОМ, на якій набрано такої ж структури диференціальне рівняння

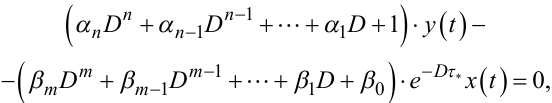(7.112)

параметри α_i, i = 1, 2,..., n; β_s, s = 1, 2,..., m та τ^* якого в процесі моделювання можна змінювати.

Підстроюючи ці параметри, домагаємось виконання умови

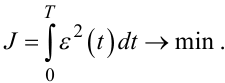(7.113)

Ті значення вказаних параметрів , які задовольняють умову (7.113), і приймаємо за оцінки відповідних коефіцієнтів a_i, b_s , τ_З.

Проте слід зазначити, що ця задача належить до класу некоректних, оскільки експонента з аргументом, що запізнюється, не може бути представлена однозначно, а розраховується шляхом розкладення в зрізаний ряд з наперед невідомою кількістю членів, оскільки запізнення теж є невідомим.

Завершимо цей підрозділ навчального посібника тим, як можна знайти математичну модель об'єкта з розподіленими параметрами у вигляді його імпульсної перехідної характеристики g(t) з врахуванням запізнення τ_З в разі, якщо і вхідний x(t), і вихідний y(t) сигнали цього об'єкта є стаціонарними випадковими процесами. У цьому випадку структурна схема об'єкта матиме вигляд, зображений на рис. 7.11.

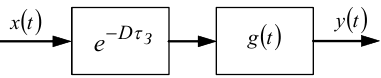
Рисунок 7.11 — Структурна схема об'єкта з розподіленими параметрами у вигляді послідовного з'єднання ланки чистого запізнення і ланки з імпульсною перехідною характеристикою g(t)

Як показано в другій частині цього навчального посібника, стаціонарні випадкові процеси x(t), y(t) у цьому випадку входять до рівняння Вінера-Хопфа кореляційною R_x(τ) та взаємною кореляційною R_yx(τ) функціями.

Користуючись тим же підходом, який використано у другій частині навчального посібника, легко показати, що рівняння Вінера-Хопфа у випадку об'єкта з розподіленими параметрами матиме вигляд:

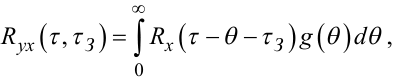(7.114)

в якому τ, θ є змінними, а τ_З є параметром, який легко знаходиться з графіків R_x(τ), R_yx(τ) (рис. 7.12).

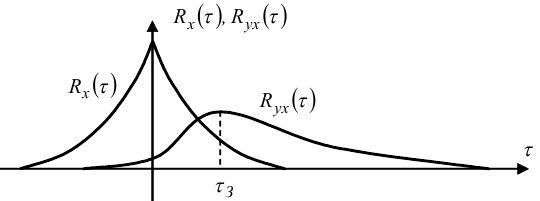
Рисунок 7.12 — Можливий варіант графіків функцій R_x(τ), R_yx(τ)

Підставляючи значення τ_З в рівняння (7.114) і розв'язуючи це рівняння одним із методів, наведених в другій частині навчального посібника, знайдемо функцію g(t) для подання об'єкта з розподіленими параметрами у вигляді структури, зображеної на рис. 7.11.