9.2 Математичні моделі нелінійних динамічних систем з релейними елементами

Структуру будь-якої замкненої нелінійної динамічної системи з одним релейним елементом і з негативним зворотним зв'язком завжди можна привести до вигляду, наведеного на рис. 9.3, де РЕ — релейний елемент, а ЛЧ — сукупність усіх елементів з лінійними характеристиками «вхід — вихід».

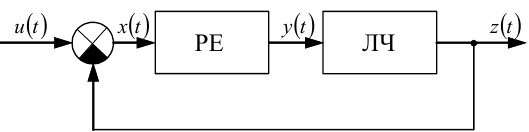
Рисунок 9.3 — Структурна схема замкненої нелінійної динамічної системи з одним релейним елементом і з негативним зворотним зв'язком

Якщо перетворити за Лапласом сигнали u(t), x(t), y(t), z(t) та алгебраїчні і диференціальні чи інтегральні рівняння, що описують лінійну частину ЛЧ, тобто перевести процес створення математичної моделі на комплексну площину, то структурну схему, наведену на рис. 9.3, можна привести до вигляду, наведеного на рис. 9.4, де W(p) — передаточна функція ЛЧ.

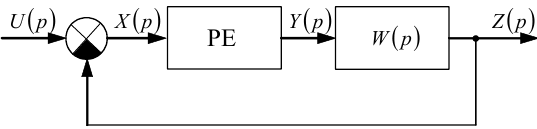
Рисунок 9.4 — Структурна схема замкненої нелінійної динамічної системи з одним релейним елементом і з негативним зворотним зв'язком на комплексній площині

Для схеми на рис. 9.4 цілком очевидними є такі співвідношення:

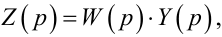(9.12)

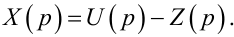(9.13)

Що ж до зв'язку між сигналами x, y та характеристикою РЕ на комплексній площині, то формально його можна записати як

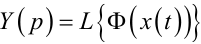(9.14)

у випадку математичної моделі РЕ у вигляді (9.1), де L{•} — оператор Лапласа;

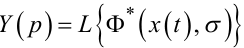(9.15)

— у випадку математичної моделі РЕ у вигляді (9.2);

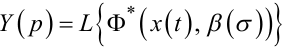(9.16)

— у випадку математичної моделі РЕ у вигляді (9.11).

Зв'язуючи між собою співвідношення (9.12), (9.13) і (9.14) або (9.15) чи (9.16), матимемо для сигналу X(p) на вході РЕ:

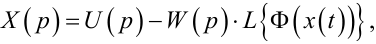(9.17)

або

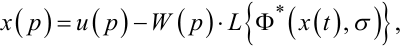(9.18)

або

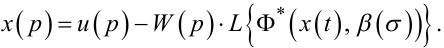(9.19)

Якщо ж викликає цікавість вихідний сигнал Z(p) лінійної частини нелінійної системи, то, пам'ятаючи, що

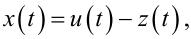(9.20)

із співвідношень (9.12) – (9.16) та (9.20) матимемо

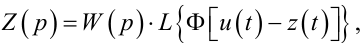(9.21)

або

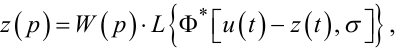(9.22)

або

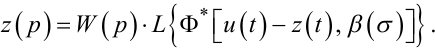(9.23)

Розглянемо процес отримання вищенаведених співвідношень на двох прикладах.

Приклад 1. Нехай нелінійною динамічною системою, процеси в якій хочемо описати, є система регулювання електрорушійної сили e(t) генератора за допомогою вібраційного регулятора на основі релейного елемента.

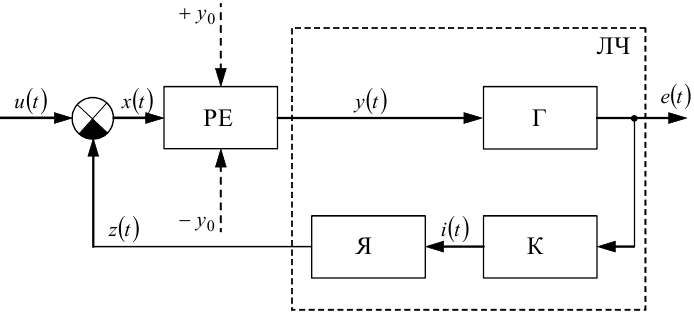
Рисунок 9.5 — Функціональна схема системи регулювання ЕРС генератора за допомогою вібраційного регулятора на основі релейного елемента

Функціональна схема такої системи матиме вигляд, наведений на рис. 9.5, на якій:

Г — генератор,

К — котушка електромагніта реле,

Я — якір електромагніта реле,

РЕ — контакти реле,

ЛЧ — лінійна частина системи.

Як бачите, котушку і якір реле віднесли до лінійної частини системи, а контакти — до релейного елемента, що формує релейну характеристику, наприклад, виду (9.1), графік якої має вигляд, показаний на рис. 9.1, б.

Фізично сигнал u(t) являє собою переміщення рухомої контактної групи реле під дією пружини, натяг якої можна змінювати, а сигнал z(t) — цепереміщення тієї ж рухомої контактної групи реле під дією якоря реле, котрий, втягуючись у котушку, переборює дію пружини.

Якщо z(t) = 0, то x(t) = u(t) > x₀ і одна група контактів реле, яку називають нормально замкнутою, замикається, подаючи напругу +y₀ на обмотку збудження генератора, викликаючи цим появу e(t).

Коли x(t) = u(t) - z(t) стає меншим x₀, нормально замкнута контактна група реле розмикається і обнуляє напругу на обмотці збудження генератора, викликаючи зменшення e(t). Зменшення e(t) приводить до зменшення z(t) і настає момент, коли x(t) = u(t) - z(t) стає більшим x₀, що приводить до замикання нормально замкнутої групи контактів реле.

Оскільки інерційність як механічної, так і електромагнітної частин реле незначна, то частота перемикань контактів реле є високою і різниця u(t) - z(t) стабілізується біля x₀, а напруга збудження генератора y(t) стабілізується біля +y₀.

Перейдемо до математичної моделі описаного вище процесу.

Зв'язок між ЕРС e(t) генератора, яка подається на вхід котушки електромагніта реле, та струмом в котушці, як відомо з теоретичних основ електротехніки, задається диференціальним рівнянням 1-го порядку, що має вигляд

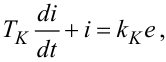(9.24)

де 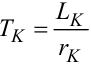— електромагнітна стала часу електромагніта, L_K — індуктивність котушки, а r_K — активний опір цієї котушки, 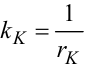— коефіцієнт передачі котушки від вхідної напруги до струму в ній.

Зв'язок між струмом i(t) в котушці електромагніта і лінійним переміщенням z(t) якоря електромагніта, як відомо з фізики, задається диференціальним рівнянням 2-го порядку, що має вигляд

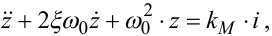(9.25)

де ξ — коефіцієнт затухання коливань якоря електромагніта, ω₀ — частота власних коливань цього якоря, а k_M — коефіцієнт передачі від струму i(t) в котушці електромагніта до лінійного переміщення z(t) його якоря.

Зв'язок між напругою yt, що подається на вхід обмотки збудження генератора, та ЕРС et його якоря, як відомо, задається диференціальним рівнянням 1-го порядку, що має вигляд

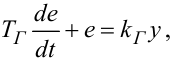(9.26)

де 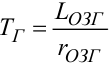— електромагнітна стала часу обмотки збудження генератора, L_ОЗГ — індуктивність обмотки збудження, r_ОЗГ — активний опір цієї обмотки, 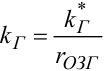— коефіцієнт передачі від напруги, що подається на вхід обмотки збудження генератора, а k^*_Г — коефіцієнт передачі від струму в обмотці збудження до ЕРС якоря генератора, який визначається з характеристики холостого ходу генератора.

Для замикання системи рівнянь, що описують систему вібраційного регулювання ЕРС генератора, функціональна схема якої наведена на рис. 9.5, залишилось лише зв'язати вхідний x(t) та вихідний x(t) сигнали релейного елемента РЕ рівнянням виду

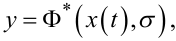(9.27)

конкретний вигляд якого залежить від наявності чи відсутності зони нечутливості та гістерезису.

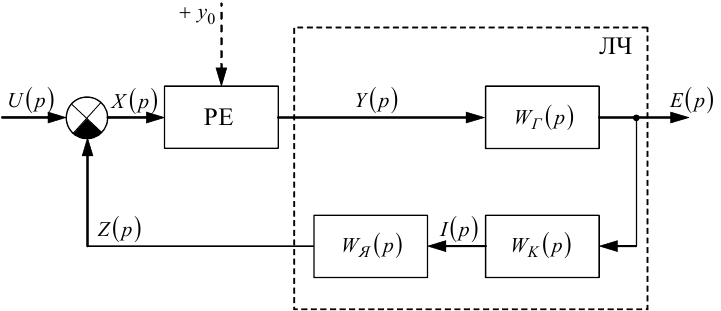
Рисунок 9.6 — Структурна схема нелінійної динамічної системи вібраційного регулювання ЕРС генератора

Перетворюючи рівняння (9.24), (9.25) та (9.26) за Лапласом і переходячи до передаточних функцій, отримаємо на комплексній площині структурну схему системи вібраційного регулювання ЕРС генератора у вигляді, показаному на рис. 9.6, де

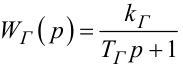(9.28)

— передаточна функція генератора,

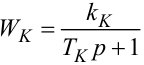(9.29)

— передаточна функція котушки електромагніта реле,

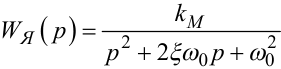(9.30)

— передаточна функція якоря електромагніта реле.

Структурна схема, що наведена на рис. 9.6, легко приводиться до загального вигляду, показаного на рис. 9.7, д

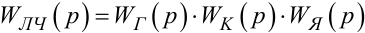(9.31)

передаточна функція лінійної частини системи, яка після підстановки у (9.31) виразів (9.28), (9.29), (9.30) набуває вигляду

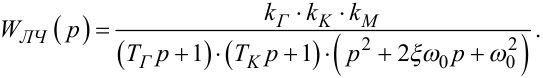(9.32)

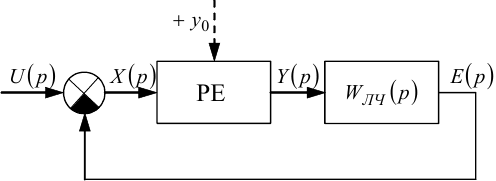
Рисунок 9.7 — Узагальнена структурна схема системи вібраційного регулювання ЕРС генератора

З врахуванням викладеного вище для системи вібраційного регулювання ЕРС генератора матимемо такі математичні моделі:

• для сигналу x(p) на вході РЕ:

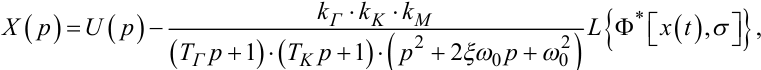(9.33)

• для вихідного сигналу Z(p) лінійної частини системи:

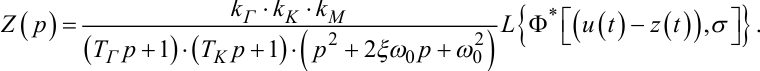(9.34)

Приклад 2. Нехай нелінійною динамічною системою, процеси в якій хочемо описати, є система стабілізації кутової швидкості ω(t) електродвигуна ЕД при змінах у часі моменту технологічного навантаження M_TH(t) електропривода, функціональна схема якої має вигляд, наведений на рис. 9.8, на якій M_Д(t) — обертальний момент якоря електродвигуна.

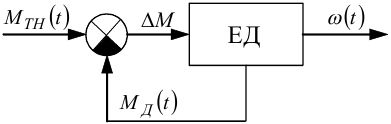
Рисунок 9.8 — Функціональна схема системи стабілізації кутової швидкості електродвигуна при змінах у часі моменту технологічного навантаження електропривода

У цій системі регулювання немає релейного елемента в явному вигляді, але він неявно формується у зв'язку з наявністю так званого сухого тертя, за рахунок якого створюється момент Ф(ω), котрий не дозволяє почати рух в системі до тих пір, поки M_Д не стане більшим за Ф(ω), і завжди має знак, протилежний знаку M_Д. Тобто, у цьому випадку, за рахунок ефекту сухого тертя, маємо замість функціональної схеми, наведеної на рис. 9.8, функціональну схему, наведену на рис. 9.9, на якій момент Ф^*(ω,σ) що виникає за рахунок сухого тертя, описується співвідношенням, що має вигляд

(9.35)

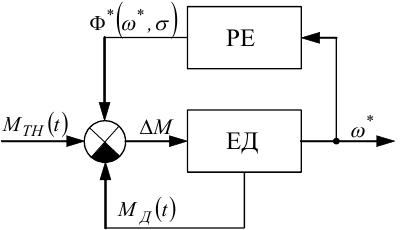
Рисунок 9.9 — Функціональна схема системи стабілізації кутової швидкості електродвигуна при змінах у часі моменту технологічного навантаження та при врахуванні сухого тертя

Якби не було сухого тертя і в'язкого демпферування, то модель руху електричного двигуна, як відомо, мала б вигляд

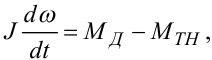(9.36)

де ω — кутова швидкість обертання вала ротора електродвигуна, а J — приведений до цього вала момент інерції махових мас, з ним з'єднаних.

Але при наявності гальмівних складових, обумовлених в'язким демпферуванням та сухим тертям, для моделювання руху електродвигуна замість лінійного рівняння (9.36) необхідно використовувати більш складне нелінійне рівняння

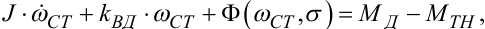(9.37)

в якому k_ВД — коефіцієнт в'язкого демпферування, а нижній індекс «СТ» біля кутової швидкості ω означає, що розглядається її значення, яке враховує вплив сухого тертя.

Рівняння (9.37) легко приводиться до виду

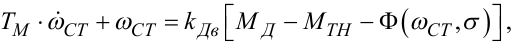(9.38)

де 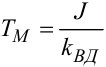— електромеханічна стала часу електродвигуна, а 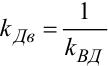— коефіцієнт передачі електродвигуна від моменту до кутової швидкості з врахуванням в'язкого демпферування.

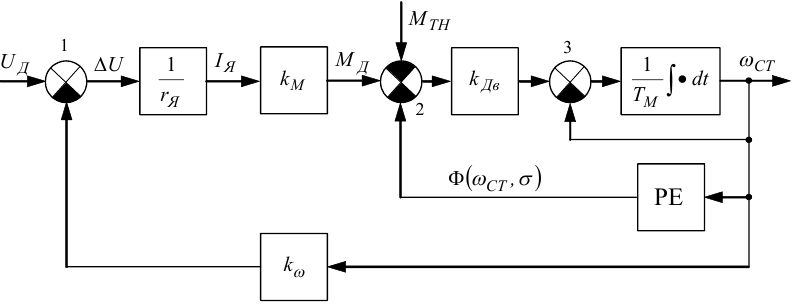
Рисунок 9.10 — Структурна схема в часовій області електричного двигуна, навантаженого моментом M_TH, модель якого враховує в'язке демпферування і сухе тертя

Легко бачити, що графічний образ рівняння (9.38) має вигляд, наведений на рис. 9.10, в якому враховано те, що

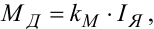(9.39)

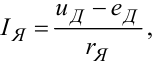(9.40)

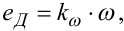(9.41)

де I_Я — струм якоря, e_Д — ЕРС його обертання, u_Д — напруга, що при- кладена до його обмотки, r_Я — активний опір цієї обмотки, а k_M і k_ω — коефіцієнти, значення яких можна знайти у будь-якому підручнику з електропривода.

Суміщаючи на схемі рис. 9.10 1-ий суматор з 2-им і позбавляючись від 3-го суматора та переходячи на комплексну площину, матимемо схему, що зображена на рис. 9.11.

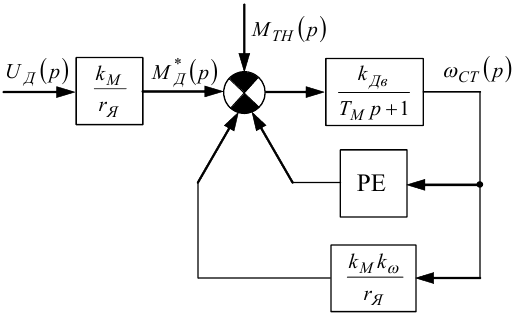
Рисунок 9.11 — Структурна схема на комплексній площині електричного двигуна, навантаженого моментом M_TH, модель якого враховує в'язке демпферування і сухе тертя

У свою чергу, пам'ятаючи, що на схемі (рис. 9.11) ланка з передаточною функцією

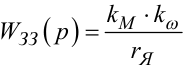(9.42)

задає негативний зворотний зв'язок для ланки з передаточною функцією

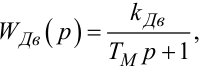(9.43)

цю схему можна легко привести до схеми, зображеної на рис. 9.12, на якій

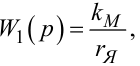(9.44)

a

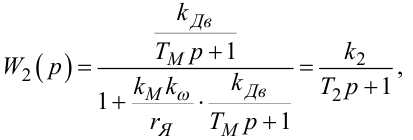(9.45)

де

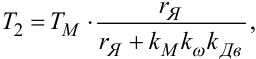(9.46)

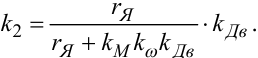(9.47)

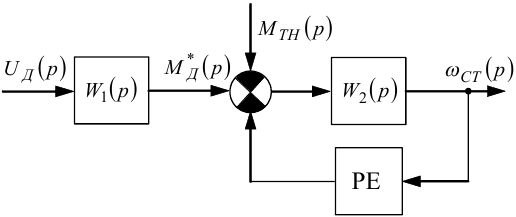
Рисунок 9.12 — Узагальнена структурна схема на комплексній площині електричного двигуна, навантаженого моментом M_TH, модель якого враховує в'язке демпферування і сухе тертя

А далі вчинимо так.

Спочатку запишемо чому дорівнюватиме різниця M^*_Д - M_TH. Зі схеми (рис. 9.12) видно, що

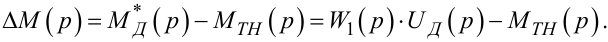(9.48)

Очевидно, що аналогом рівняння (9.48) є рівняння

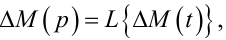(9.49)

в якому

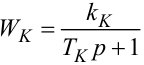(9.50)

є оберненим перетворенням Лапласа виразу, який стоїть в правій частині рівняння (9.48).

Враховуючи співвідношення (9.49) і (9.50), маємо право структурну схему рис. 9.12 подати у вигляді, зображеному на рис. 9.13.

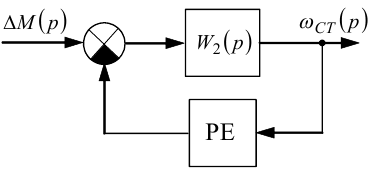
Рисунок 9.13 — Еквівалентна структурна схема на комплексній площині електричного двигуна, навантаженого моментом M_TH, модель якого враховує в'язке демпферування і сухе тертя

Із схеми рис. 9.13 видно, що вже звели початкову структуру нелінійної динамічної системи, графічно заданої на рис. 9.10, до структури, що складається лише з лінійної частини і релейного елемента.

Але для аналізу релейних систем зручніше, щоб суматор був на вході релейного елемента. Тож здійснимо ще одне структурне перетворення схеми, показаної на рис. 9.13, — перенесемо суматор з входу ланки з передаточною функцією W₂(p) на її вихід. В результаті цього переносу отримаємо схему, зображену на рис. 9.14.

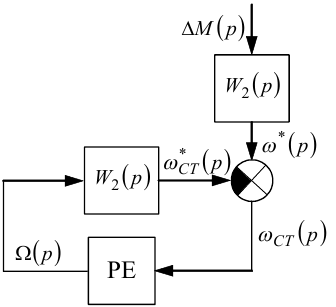
Рисунок 9.14 — Структурна схема, яка є еквівалентною схемі, показаній на рис. 9.13, але з суматором, перенесеним на вхід релейного елемента

На рис. 9.14 маємо, як і в схемі на рис. 9.3, класичне для аналізу з'єднання релейного елемента та лінійної частини.

Для цієї схеми є справедливим:

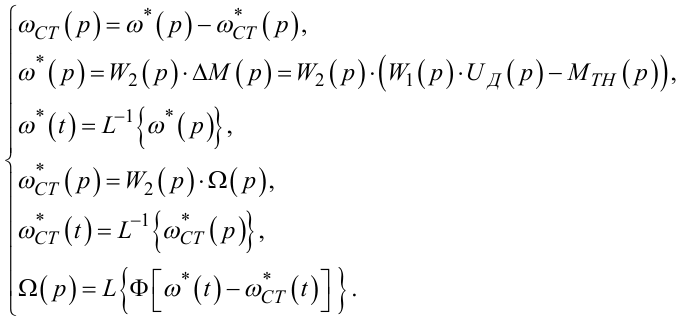(9.51)

Система рівнянь (9.51) і є математичною моделлю електричного двигуна, навантаженого моментом M_TH, моментом від в'язкого демпферування k_ВД·ω та моментом від сухого тертя Ф(ω,σ), з приведеним до входу релейного елемента суматором.

Як бачимо, синтез цієї моделі зводиться до визначення передаточної функції лінійної частини нелінійної динамічної системи і перерахунку її зовнішніх сигналів до входу релейного елемента.