9.3 Аналіз процесів в нелінійних динамічних системах з релейними елементами
Нехай релейний елемент РЕ (рис. 9.15, а) має характеристику, що зображена на рис. 9.1, а, яка для зручності повторена на рис. 9.15, б.
На рис. 9.15 легко бачити, що яким би не був вхідний сигнал x(t) (рис. 9.15, в) релейного елемента, його вихідний сигнал y(t) завжди являтиме собою послідовність імпульсів однієї і тієї ж висоти y0, знак кожного із яких визначатиметься знаком функції x(t) між двома сусідніми значеннями tk і tk+1 аргументу t, в яких ця функція перетинає вісь абсцис, а протяжність
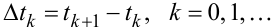 |
(9.52) |
дорівнюватиме відрізку часу між цими сусідніми його значеннями tk і tk+1.
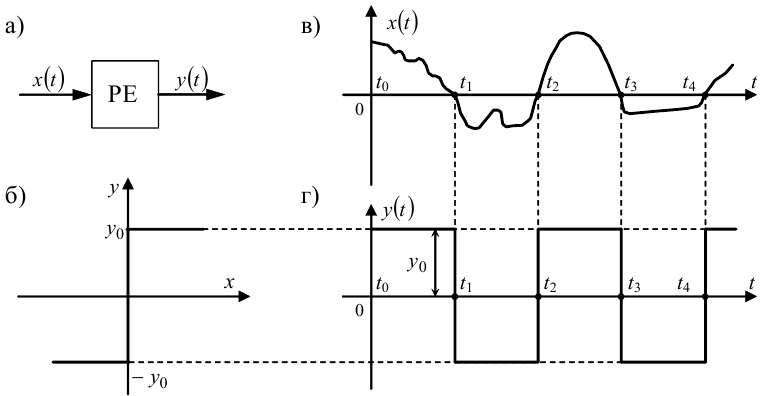
Рисунок 9.15 — Графічна інтерпретація формування вихідного сигналу релейного елемента без зони нечутливості і гістерезису
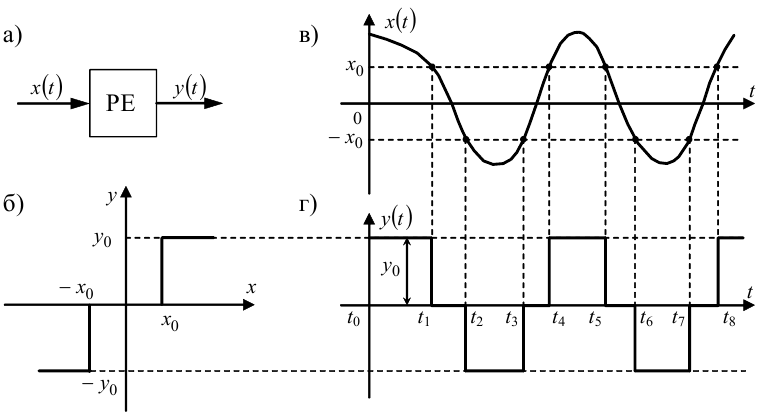
Рисунок 9.16 — Графічна інтерпретація формування вихідного сигналу релейного елемента з зоною нечутливості, але без гістерезису
Якщо ж релейний елемент РЕ (рис. 9.16, а) має характеристику, що зображена на рис. 9.1, б, яка для зручності повторена на рис. 9.16, б, то, очевидно, що його реакцією на вхідний сигнал x(t) (рис. 9.16, в) буде вихідний сигнал y(t), зображений на рис. 9.16, г.
Ми знову маємо знакозмінну послідовність імпульсів однакової висоти y0, але протяжність кожного з них буде меншою від значення, що задається формулою (9.52). А між кожною парою сусідніх імпульсів з'являється проміжок часу, в який вихідний сигнал y(t) релейного елемента дорівнює нулю.
Тепер розглянемо випадок, коли релейний елемент РЕ (рис. 9.17, а) має характеристику, що зображена на рис. 9.1, в, яка для зручності повторена на рис. 9.17, б
Очевидно, що у цьому випадку реакцією релейного елемента РЕ на вхідний сигнал x(t) (рис. 9.17, в) буде вихідний сигнал y(t), зображений на рис. 9.17, г.
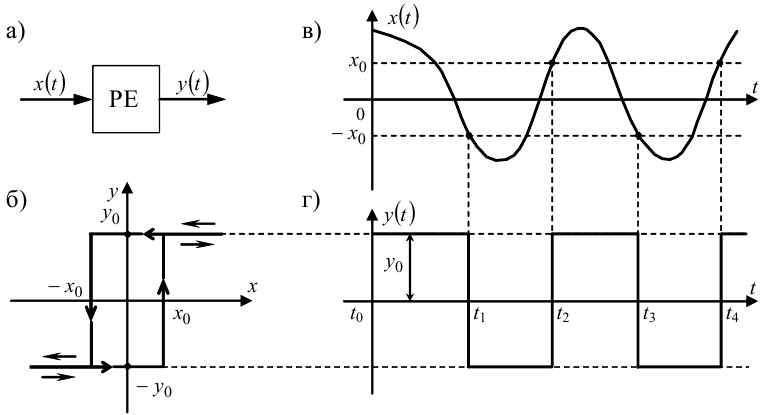
Рисунок 9.17 — Графічна інтерпретація формування вихідного сигналу релейного елемента з гістерезисом, але без зони нечутливості
На відміну від попереднього, у цьому випадку не буде нульових значень вихідного сигналу y(t), але на відміну від випадку, який розглянули найпершим, кожний наступний імпульс буде з'являтись не в момент перехо ду сигналу x(t) через нуль, а з запізненням, значення якого залежатиме як від форми сигналу x(t), так і від ширини 2x0 гістерезисної петлі.
Останнім розглянемо випадок, коли релейний елемент має характеристику, що зображена на рис. 9.1, г, яка для зручності повторена на рис. 9.18, б.
Очевидно, що і в цьому випадку вихідний сигнал y(t) релейного елемента матиме вигляд знакозмінної послідовності імпульсів однакової висоти, але, як і у випадку, розглянутому другим, тут матимуть місце проміжки часу з нульовим значенням вихідного сигналу y(t) між сусідніми імпульсами, і, одночасно, як і у випадку, розглянутому третім, тут матиме місце запізнення появи кожного наступного імпульсу.
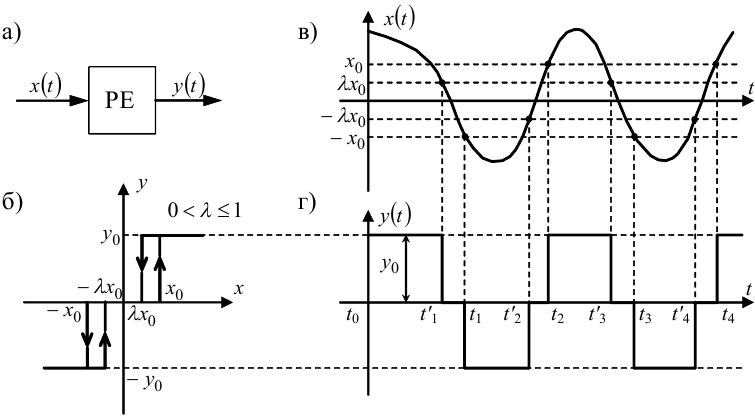
Рисунок 9.18 — Графічна інтерпретація формування вихідного сигналу релейного елемента з зоною нечутливості і гістерезисом
Усі розглянуті випадки об'єднує одне — релейний елемент створює на вході лінійної частини нелінійної динамічної системи знакозмінну послідовність імпульсів однакової висоти. А це, в свою чергу, означає, що вихідний сигнал лінійної частини нелінійної системи, який одночасно є і складовою вхідного сигналу релейного елемента (рис. 9.3), можна знайти як суму реакцій лінійної частини нелінійної динамічної системи на кожний із імпульсів вхідної імпульсної знакозмінної послідовності.
Тож, як бачимо, задача аналізу суттєво нелінійної динамічної системи з релейним елементом зводиться до:
1) пошуку моментів tk, k = 0,1,... переключення релейного елемента під дією вхідного сигналу x(t);
2) перетворення за Лапласом суми імпульсів знакозмінної послідовності, яка з виходу РЕ надходить на вхід лінійної частини системи;
3) оберненого перетворення за Лапласом вихідного сигналу лінійної частини системи, заданого в залежності від форми характеристики релейного елемента одним із співвідношень (9.21), (9.22) або (9.23).
Для конкретизації цього поки що загального алгоритму розв'язання задачі аналізу суттєво нелінійних динамічних систем з релейним елементом припустимо спочатку, що нам уже відомі моменти tk, k = 0,1,... переключення релейного елемента, що має характеристику y = Ф(x), показану рис. 9.15, б.
Тоді модель імпульсу висотою (-1)k · y0 і протяжністю Δtk (9.52) у часовій області матиме вигляд:
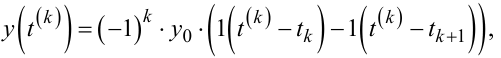 |
(9.53) |
де 1(t) — це одинична східчаста функція, для якої справедливо
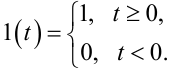 |
(9.54) |
Про що уже зазначалось раніше, але для зручності повторили і тут.
Перетворюючи за Лапласом вираз (9.53), отримаємо
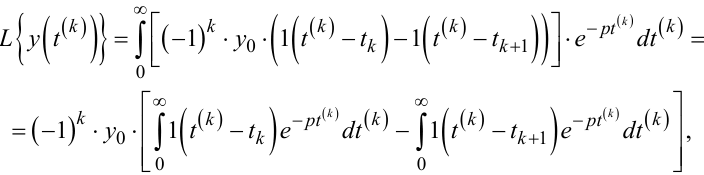 |
(9.55) |
Роблячи заміну змінних у першому інтегралі θ = t(k) - tk, а у другому інтегралі τ = t(k) - tk+1, із (9.55) отримаємо
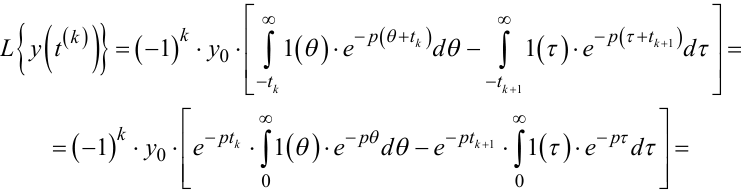
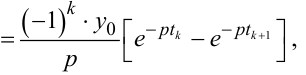 |
(9.56) |
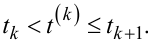 |
Узагальнюючи результат (9.56) на суму із n імпульсів, що слідують один за одним щільно, тобто без проміжків, матимемо:
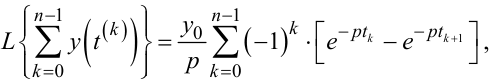 |
(9.57) |
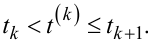
Співвідношення, очевидно, буде справедливим для зображення за Лапласом вихідного сигналу релейного елемента з характеристикою, показаною на рис. 9.15, б. Тобто справедливою є тотожність
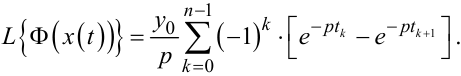 |
(9.58) |
Пам'ятаючи, що
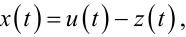 |
(9.59) |
що випливає із структурної схеми рис. 9.3, із співвідношень (9.21) і (9.58) матимемо:
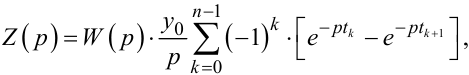 |
(9.60) |
або
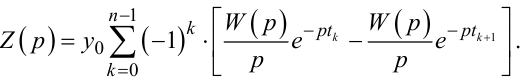 |
(9.61) |
У першій частині цього навчального посібника було показано, що зображення за Лапласом перехідної характеристики h(t) системи має вигляд:
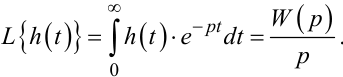 |
(9.62) |
Знайдемо, чому дорівнюватиме зображення за Лапласом зміщеної на час tk перехідної характеристики цієї ж системи.
З означення —
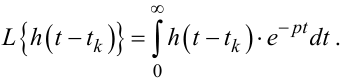 |
(9.63) |
Здійснимо у (9.63) заміну змінної. Нехай
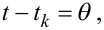 |
(9.64) |
тоді
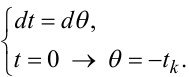 |
(9.65) |
З врахуванням (9.64) і (9.65) з (9.63) отримаємо:
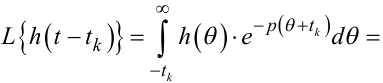 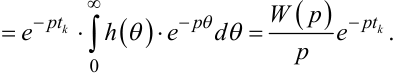 |
(9.66) |
Отримавши співвідношення (9.66), отримуємо водночас і право записати його з використанням оберненого перетворення Лапласа у такому вигляді:
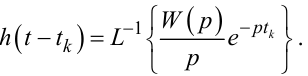 |
(9.67) |
Якщо маємо зображення за Лапласом вихідного сигналу Z(p), то, за означенням, його оригіналом у часовій області буде
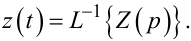 |
(9.68) |
Підставляючи у (9.68) вираз (9.61), матимемо:
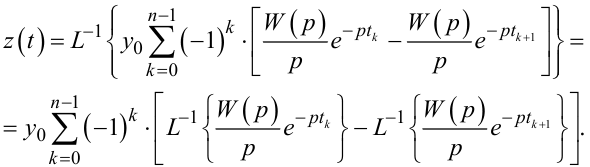 |
(9.69) |
З врахуванням (9.67), співвідношення (9.69) можна переписати так:
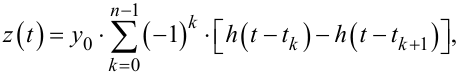 |
(9.70) |
або
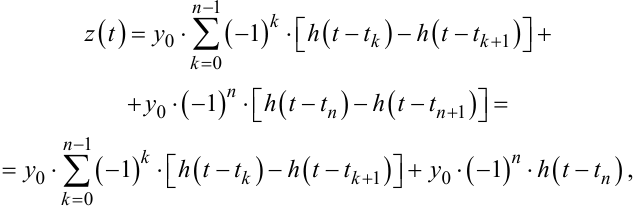 |
(9.71) |
Враховуючи, що
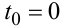 |
(9.72) |
(це випливає з рис. 9.15), рівняння (9.71) можна переписати і так:
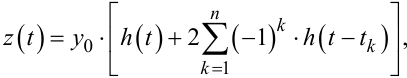 |
(9.73) |
Для наочності розпишемо вираз (9.73) для трьох значень n
Нехай n = 0, тоді
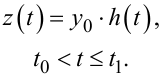 |
(9.74) |
Нехай n = 1, тоді:
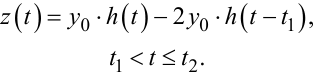 |
(9.75) |
Нехай n = 2, тоді:
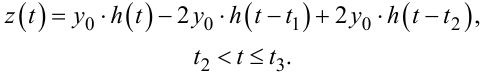 |
(9.76) |
А знаючи вихідний сигнал лінійної частини системи z(t), при заданому керувальному сигналі u(t), за допомогою виразу (9.59) легко знаходимо значення x(t) сигналу на вході релейного елемента РЕ (рис. 9.3) для будь-якого моменту часу t.
Усі викладки, що присвячені отриманню математичних моделей, необхідних для аналізу нелінійних динамічних систем з релейними елементами, зроблені за умови, що відомими є моменти переключення tk, k = 0,1,... релейного елемента.
Тож, для побудови замкненого алгоритму аналізу даного класу систем необхідно цей алгоритм доповнити способом визначення моментів переключення релейного елемента.
Із рис. 9.15 легко бачити, що моменти переключення tk, k = 0,1,... релейного елемента, на вхід якого надходить сигнал xt, є коренями рівняння
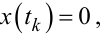 |
(9.77) |
яке після підстановки в (9.77) виразу (9.59) набуває вигляду
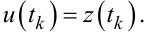 |
(9.78) |
В рівнянні (9.78), нагадаємо, u(t) — керувальний сигнал, що подається на вхід системи, а z(t) — вихідний сигнал її лінійної частини.
Із виразів (9.78) і (9.74) легко бачити, що момент t1 першого переключення РЕ після включення системи в роботу шляхом подачі керувального сигналу u(t) знаходиться з рівняння
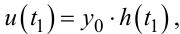 |
(9.79) |
в якому h(t) — попередньо знайдена експериментально чи оберненим перетворенням Лапласа виразу (9.62) перехідна характеристика лінійної частини системи, що аналізується.
Оскільки в проміжку часу t1 < t < t2 для сигналу z(t) справедливим є рівняння (9.75), то момент переключення t2 можна знайти з рівняння
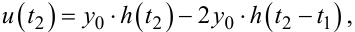 |
(9.80) |
яке отримуємо підстановкою (9.75) у (9.78).
Аналогічно, момент переключення t3 знайдемо з рівняння
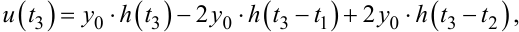 |
(9.81) |
яке отримуємо підстановкою виразу (9.76) у (9.78)
Узагальнюючи, можна стверджувати, що будь-який (n + 1)-ий момент переключення РЕ може бути знайдений з рівняння
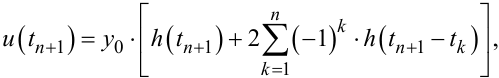 |
(9.82) |
яке отримуємо, підставляючи вираз (9.73) у (9.78).
Із рис. 9.15 видно, що вхідний сигнал x(t) релейного елемента в момент t1 першого переключення має похідну ![]() (t1) з від'ємним знаком, а в момент t1 другого переключення — з додатним знаком. І далі знаки у похідній
чергуються.
(t1) з від'ємним знаком, а в момент t1 другого переключення — з додатним знаком. І далі знаки у похідній
чергуються.
В загальному вигляді це чергування знака похідної ![]() (tk) сигналу xx(t)
в точках переключення можна задати умовою
(tk) сигналу xx(t)
в точках переключення можна задати умовою
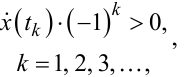 |
(9.83) |
або (з врахуванням виразу (9.59)) умовою
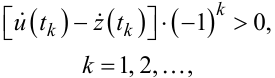 |
(9.84) |
яку називають умовою належних напрямків переключень.
Важливе зауваження: аби не пропустити якийсь момент переключення, рівняння (9.82) необхідно розв'язувати методом послідовних наближень з достатньо малим кроком ітерації.
Тепер розглянемо питання стосовно того, яких змін зазнає алгоритм аналізу релейних динамічних систем, якщо релейний елемент матиме характеристику, відмінну від показаної на рис. 9.15, б.
Почнемо розгляд з систем з релейною характеристикою, наведеною на рис. 9.17, б.
Легко бачити, що у цьому випадку знакозмінна імпульсна послідовність y(t) на виході релейного елемента РЕ має такий самий характер, як і у вже розглянутому випадку. Відмінність лише в рівнянні, за допомогою якого знаходяться моменти переключень tk, k = 1, 2,....
Із рис. 9.17, в видно, що рівняння для визначення моментів переключень tk, k = 1, 2,... у цьому випадку матиме вигляд
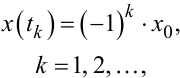 |
(9.85) |
або (з врахуванням (9.59))
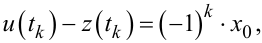 |
(9.86) |
що еквівалентно
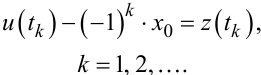 |
(9.87) |
Із того ж рис. 9.17, в видно, що умова належних напрямків переключень залишається такою ж, як і в попередньому випадку і задається тими ж виразами (9.83), (9.84).
Що ж стосується сигналу z(t) на виході лінійної частини релейної нелінійної системи даного класу, то для нього є справедливими ті ж вирази (9.73) – (9.76), що і для того випадку, для якого ці вирази отримані і які зображено на рис. 9.15.
Тепер перейдемо до аналізу релейних динамічних систем з релейними характеристиками, показаними на рис. 9.16, б і рис. 9.18, б.
Легко бачити, що знакозмінна імпульсна послідовність y(t) на виході релейного елемента в обох цих випадках має один і той же характер, що не дивно, оскільки релейну характеристику, яка наведена на рис. 9.16, б, можна отримати з релейної характеристики, що наведена на рис. 9.18, б, при λ = 1.
Тож достатньо розглянути випадок, показаний на рис. 9.18. Зробимо це.
Нехай t1, t2, t3,... — це моменти переключення, які виникають у моме- нти переходу сигналу x(t) через пороги ±x0, а t'1, t'2, t'3... — через пороги ±λx0.
Із рис. 9.18, в можна бачити, що усі ці моменти є коренями рівнянь:
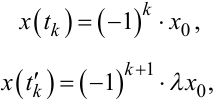 |
(9.88) (9.89) |
які за допомогою виразу (9.59) трансформуються у рівняння:
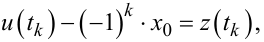 |
(9.90) |
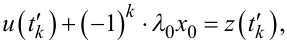 |
(9.91) |
Очевидно (рис. 9.18, в), що умова належних напрямків переключень для обох цих випадків буде задаватись однаковими за структурою виразами, аналогічними (9.83) і (9.84), а саме:
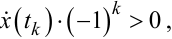 |
(9.92) |
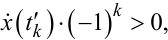 |
(9.93) |
або (з врахуванням виразу (9.59)):
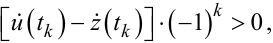 |
(9.94) |
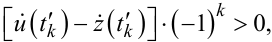 |
(9.95) |
Дивлячись на рівняння (9.90), (9.91), бачимо, що при заданих u(t), x0, для їх розв'язання відносно tk і t'k, k = 1, 2,... необхідно знати вихідний сигнал z(t) лінійної частини (ЛЧ) релейної динамічної системи.
Перш ніж перейти до виведення розрахункових співвідношень для сигналу z(t) звертаємо увагу на те, що він формується лише за рахунок впливуімпульсів висотою (-1)k · y0 між моментами tk і t'k+1, оскільки між моментами t'k+1 і tk+1 вхідний сигнал y(t) дорівнює нулю.
Як знайти реалізацію z(t) ЛЧ системи на таку послідовність імпульсів уже відомо (див. вирази (9.53) – (9.71), в яких усюди tk+1 необхідно замінити на t'k+1). Тобто маємо право записати:
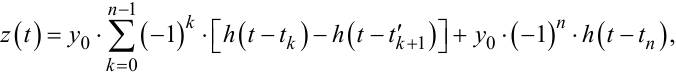 |
(9.96) |
А для проміжку часу t'n+1) < t ≤ tk+1) рівняння (9.96) набуває вигляду
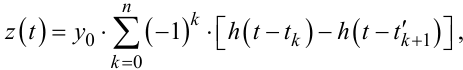 |
(9.97) |
Пам'ятаючи, що t0 = 0, розкриваємо (9.96), (9.97) для трьох значень n.
Нехай n = 0, тоді
для t0 < t ≤ t'1:
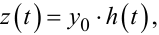 |
(9.98) |
для t'1 < t ≤ t'1:
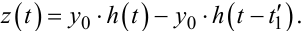 |
(9.99) |
Нехай n = 1, тоді:
для t1 < t ≤ t'2:
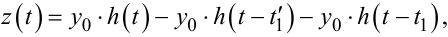 |
(9.100) |
для t'2 < t ≤ t2:
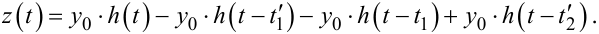 |
(9.101) |
Нехай n = 2, тоді:
для t2 < t ≤ t'3:
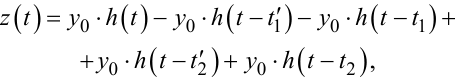 |
(9.102) |
для t'3 < t ≤ t3:
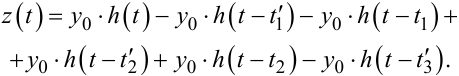 |
(9.103) |
Для знаходження моменту переключення t'1 необхідно у вираз (9.91) підставити значення z(t) із (9.98) і розв'язати відносно t'1 отримане рівняння
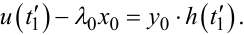 |
(9104.) |
Аналогічно, для знаходження моменту переключення t1 необхідно у вираз (9.90) підставити значення z(t) із (9.99) і розв'язати відносно t1 отримане рівняння
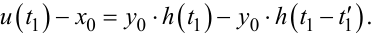 |
(9.105) |
Для знаходження наступних моментів переключень необхідно рекурентно продовжити цей процес отримання і розв'язання рівнянь спочатку стосовно t'k, а потім стосовно tk, починаючи з k = 2 .
Очевидно, що всі отримані в цьому випадку співвідношення будуть справедливими і при = 1. А саме при такому значення λ релейний елемент, зображений на рис. 9.18, а, з релейною характеристикою, наведеною на рис. 9.18, б, перетворюється на релейний елемент, зображений на рис. 9.16, а, з релейною характеристикою, наведеною на рис. 9.16, б.
Тож, для аналізу релейних динамічних систем з релейною характеристикою, зображеною на рис. 9.18, б, необхідно використовувати всі отримані вище математичні моделі, починаючи з (9.88), поклавши λ = 1 в тих із них, які цей параметр мають у своїй структурі.
На завершення розділу зауважимо, що аналіз релейних динамічних систем з несиметричними релейними характеристиками, наприклад, такими, як показано на рис. 9.19, майже нічим не відрізняється від вищевикладеного.
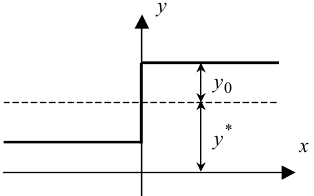
Рисунок 9.19 — Приклад несиметричної релейної характеристики
Єдине, чим доповнюється алгоритм аналізу таких систем, є те, що у вихідному сигналі z(t) лінійної частини системи з'являється додатковий член
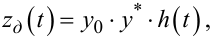 |
(9.106) |
який характеризує реакцію лінійної частини системи з перехідною характеристикою h(t) на усталений вплив y* релейного елемента, характеристика якого центрована цим значенням. Тобто у цьому випадку для сигналу z(t) замість моделей (9.70) і (9.71) необхідно використовувати моделі, відповідно:
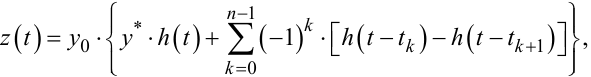 |
(9.107) |
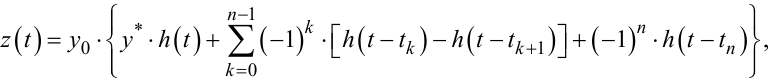 |
(9.108) |
Аналогічні поправки до отриманих моделей сигналу z(t) будуть мати місце і при несиметризації інших із розглянутих симетричних релейних характеристик.


